Introducción a la ecuación de la recta, fundamentos
Summary
TLDREn este video introductorio, se explica la ecuación de la recta y sus conceptos fundamentales. Se aborda la inclinación de las rectas, su relación con la pendiente, y cómo estas cortan los ejes X e Y. Se menciona la ecuación punto-pendiente, que describe cómo la pendiente determina la inclinación de la recta y cómo el valor de 'b' indica el punto de corte con el eje Y. Este video es el comienzo de un curso más amplio sobre las ecuaciones de la recta, invitando a los espectadores a seguir aprendiendo y participar activamente en el canal.
Takeaways
- 🎓 Introducción al curso sobre la ecuación de la recta, enfocada en explicar su concepto y generalidades.
- 📐 Todas las rectas tienen una inclinación, que es uno de los aspectos más importantes a considerar.
- 📊 Una recta pasa por infinidad de puntos, como se ejemplifica con los puntos mencionados (menos 80, menos 61, menos 42).
- ⬆️⬇️ Las rectas pueden subir o bajar dependiendo de la dirección en la que se observen (de izquierda a derecha).
- 📝 La ecuación punto-pendiente es fundamental: y = mx + b, donde m es la pendiente y b es el punto de corte con el eje y.
- 🔢 El valor de b (punto de corte con el eje y) cambia según dónde la recta corte dicho eje, independientemente de la inclinación.
- 📐 La pendiente determina la inclinación de la recta y permite calcular el ángulo que forma con el eje x.
- ✖️ La mayoría de las rectas cortan tanto el eje y como el eje x, a excepción de las rectas horizontales y verticales.
- 🚴♂️ Las rectas pueden ser vistas como subiendo o bajando si se observa de izquierda a derecha, similar a una bicicleta en una pendiente.
- 🎥 Invitación a los espectadores a seguir el curso completo y a interactuar con el contenido a través de likes, comentarios y compartiendo el video.
Q & A
¿Qué es la ecuación de la recta y por qué es importante?
-La ecuación de la recta es una representación matemática que describe la relación entre los puntos en un plano. Es importante porque permite identificar la inclinación y el punto de corte de una recta con los ejes de coordenadas.
¿Qué es la inclinación de una recta y cómo se relaciona con la ecuación de la recta?
-La inclinación de una recta, también conocida como pendiente, es la medida de su 'steepness' o 'tendencia'. En la ecuación de la recta, la pendiente se representa con la letra 'm' y es crucial para determinar la dirección en la que la línea se inclina.
¿Cuál es la forma de la ecuación de la recta en términos de 'y = mx + b'?
-La ecuación de la recta en la forma 'y = mx + b' representa la relación entre 'y' (la coordenada y), 'x' (la coordenada x), 'm' (la pendiente) y 'b' (el punto de corte con el eje y). Esta ecuación se llama ecuación punto-pendiente.
¿Cómo se determina si una recta está subiendo o bajando al observarla de izquierda a derecha?
-Si al observar una recta de izquierda a derecha, el valor de 'y' aumenta, entonces la recta está subiendo. Si el valor de 'y' disminuye, la recta está bajando.
¿Qué es el punto de corte y cómo se identifica en la ecuación de la recta?
-El punto de corte es el punto en el que la recta intersecta con uno de los ejes de coordenadas. En la ecuación 'y = mx + b', 'b' representa el punto de corte con el eje y.
¿Qué son las rectas horizontales y cómo se identifican en el plano cartesiano?
-Las rectas horizontales son aquellas que no tienen inclinación y, por lo tanto, su pendiente 'm' es cero. En el plano cartesiano, estas rectas son paralelas al eje x y solo cortan el eje y.
¿Qué son las rectas verticales y cómo se diferencian de las demás rectas?
-Las rectas verticales son aquellas que cortan solo el eje x y su pendiente 'm' es infinita. Estas rectas son perpendiculares a las rectas horizontales y no tienen un punto de corte con el eje y.
¿Cómo se relaciona la pendiente de una recta con el ángulo que forma con el eje x?
-La pendiente de una recta está relacionada con el ángulo que forma con el eje x a través de la función tangente. El ángulo se halla aplicando la tangente a la pendiente de la recta.
¿Por qué todas las rectas tienen una inclinación, incluso si parecen no cortar el eje x?
-Todas las rectas tienen una inclinación porque representan una relación entre dos variables que puede ser directa o inversa. Aunque algunas rectas no cortan el eje x en el rango de visualización,理论上她们仍然会在某一点上与x轴相交,因为它们无限延伸。
¿Cómo se puede encontrar el ángulo que forma una recta con el eje x si se conoce su pendiente?
-Para encontrar el ángulo que forma una recta con el eje x, se utiliza la fórmula del seno inverso (arcsin) o la tangente inversa (arctan) de la pendiente de la recta.
¿Cómo se puede graficar una recta dada su ecuación punto-pendiente?
-Para graficar una recta dada su ecuación punto-pendiente, se identifican el punto de corte 'b' y se utiliza la pendiente 'm' para determinar el cambio en 'y' por cada unidad de cambio en 'x', a partir del punto de corte.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
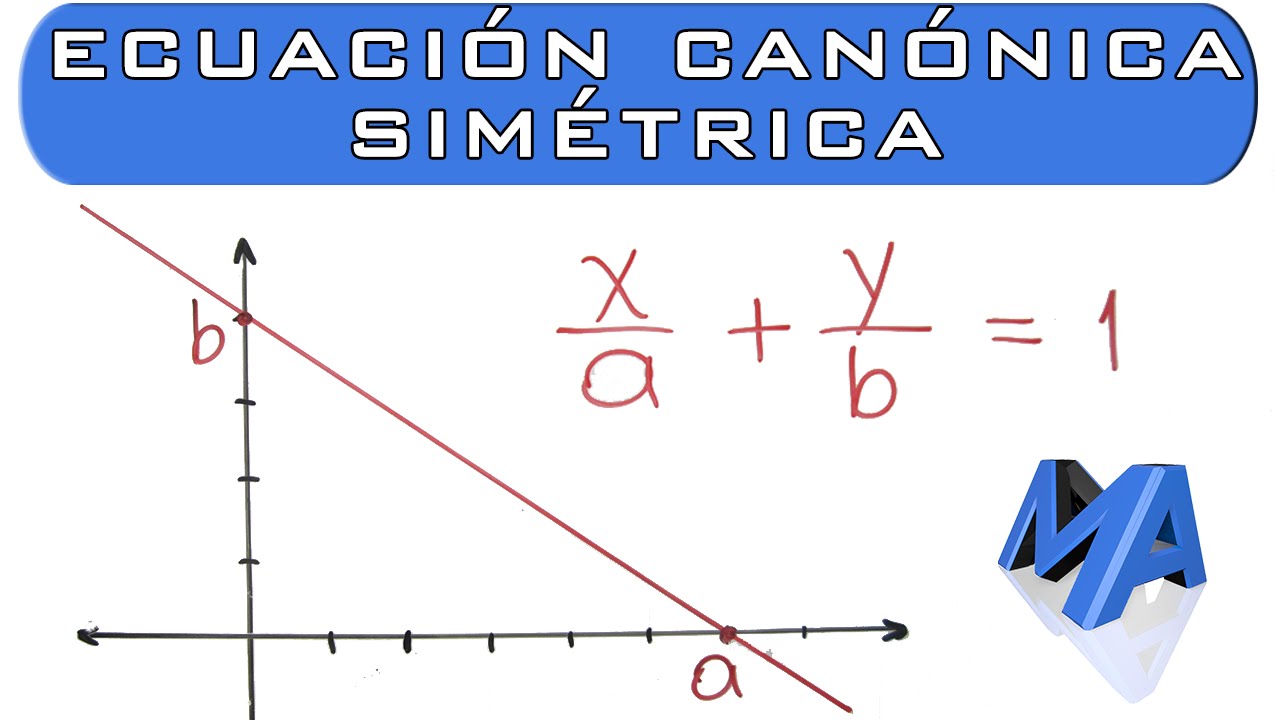
Ecuación canónica o simétrica de la recta

Tipos de rectas: Horizontal, vertical e inclinada

Conceptos Básicos de Geometría

Rectas paralelas y perpendiculares | Ecuación de la recta | La Prof Lina M3

Ex 6: Conic Section: Parabola with Horizontal Axis and Vertex NOT at the Origin (Right)

70. Ecuación vectorial de una recta en el plano y el espacio EXPLICACION
5.0 / 5 (0 votes)
