Part 1: Formal Definition of a Limit
Summary
TLDRThis video introduces the formal definition of limits in calculus. It begins with an informal explanation, showing how a limit exists when the function approaches the same value from both sides of a point. The video then dives into the precise mathematical definition involving epsilon (vertical distance) and delta (horizontal distance) to prove that a limit exists. Through an example, the video demonstrates the process of finding a relationship between epsilon and delta and using it to rigorously prove a limit. The goal is to equip viewers with the understanding to formally prove limits exist.
Takeaways
- 😀 The concept of a limit involves approaching a certain value (C) from both the left and right sides, with the function value approaching a particular point (L).
- 😀 A limit exists if the function approaches the same value from both sides, even if the function is not defined at the point C (e.g., a hole in the graph).
- 😀 The formal definition of a limit involves the relationship between epsilon (vertical distance) and delta (horizontal distance) to prove that a limit exists.
- 😀 Epsilon (ε) represents a vertical distance from the limit L, and delta (δ) represents a horizontal distance from the point C.
- 😀 The goal in proving a limit is to show that for any vertical distance ε, there exists a corresponding horizontal distance δ such that the function value is within the vertical range around L.
- 😀 Graphically, if given ε (a vertical interval), we can find δ (a horizontal interval) such that any x in the interval [C-δ, C+δ] produces f(x) within [L-ε, L+ε].
- 😀 To prove a limit, you start with an inequality involving the absolute values of the difference between f(x) and L, and manipulate this inequality to match the form involving the absolute value of x - C.
- 😀 In the example of the linear function 1/3x + 1, the process involves substituting values, simplifying the absolute value expression, and establishing a relationship between ε and δ.
- 😀 The process of proving the limit involves working backwards from the desired conclusion, finding the relationship between ε and δ, and then moving forward to construct the proof.
- 😀 The final proof demonstrates that if the absolute value of (x - C) is less than δ, then the absolute value of (f(x) - L) is less than ε, confirming the limit exists.
Q & A
What is the informal definition of a limit?
-The limit of a function as x approaches a specific value exists if, as x approaches that value from both the left and right, the function values approach the same value.
How is the limit represented graphically?
-Graphically, the limit is represented by the function values approaching a specific y-value (L) as x approaches a particular x-value (C), even if the function is not defined at x = C.
What does the formal definition of a limit state?
-The formal definition states that for every ε > 0, there exists a δ > 0 such that if the distance between x and C is less than δ, the distance between f(x) and the limit L is less than ε.
What is the role of ε and δ in the formal definition of limits?
-ε (epsilon) represents a vertical distance from the limit L, and δ (delta) represents a horizontal distance from the point C. They are related in that for any given ε, a corresponding δ can be found such that the function's output stays within ε of L when x is within δ of C.
What does the absolute value in the definition of limits represent?
-The absolute value represents distance. In the definition, |x - C| represents the horizontal distance between x and C, and |f(x) - L| represents the vertical distance between f(x) and the limit L.
Why is the function value f(x) not required to be defined at x = C?
-The function does not need to be defined at x = C for the limit to exist. The limit concerns the behavior of the function as x approaches C, not the actual value of the function at C.
What is the first step in proving that a limit exists?
-The first step is to start by expressing the absolute value of f(x) - L as less than ε, and then manipulate the expression to match the form of |x - C|, which is used to establish the relationship between ε and δ.
In the example given, how is the limit of f(x) = 1/3x + 1 as x approaches 6 proven to be 3?
-In the example, the absolute value |f(x) - 3| is manipulated to match the form |x - 6|. By multiplying both sides by 3, the relationship δ = 3ε is established. This allows the proof to proceed from left to right to show that the limit is indeed 3.
How does the relationship between ε and δ allow for the proof of a limit?
-The relationship between ε and δ is key to the proof because it shows that for every vertical distance (ε), a corresponding horizontal distance (δ) exists that keeps the function values within ε of the limit L when x is within δ of C.
What is the significance of the example with the linear function 1/3x + 1?
-The example with the linear function demonstrates the process of proving a limit using the formal definition. It shows how basic algebraic manipulation, such as factoring and multiplying by constants, helps establish the necessary relationship between ε and δ.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus

LIMITE: a Ideia Fundamental do Cálculo
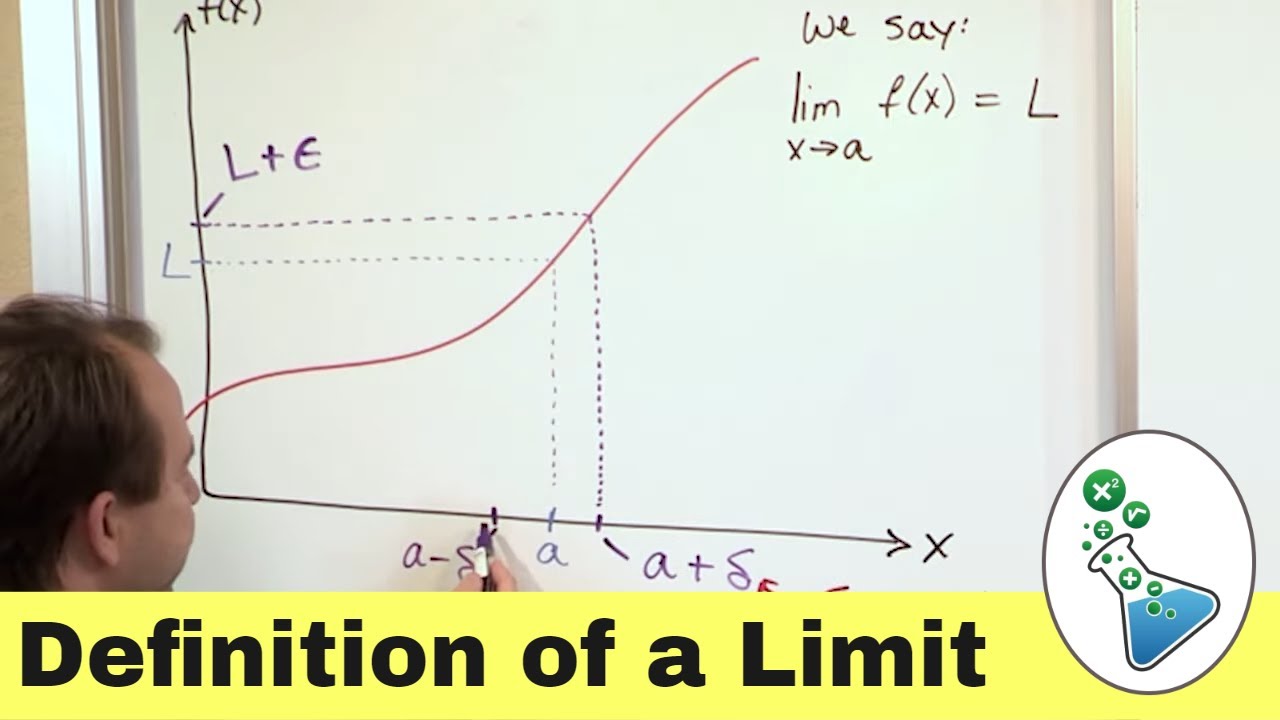
Limits in Calculus: Definition & Meaning. What is a Limit?
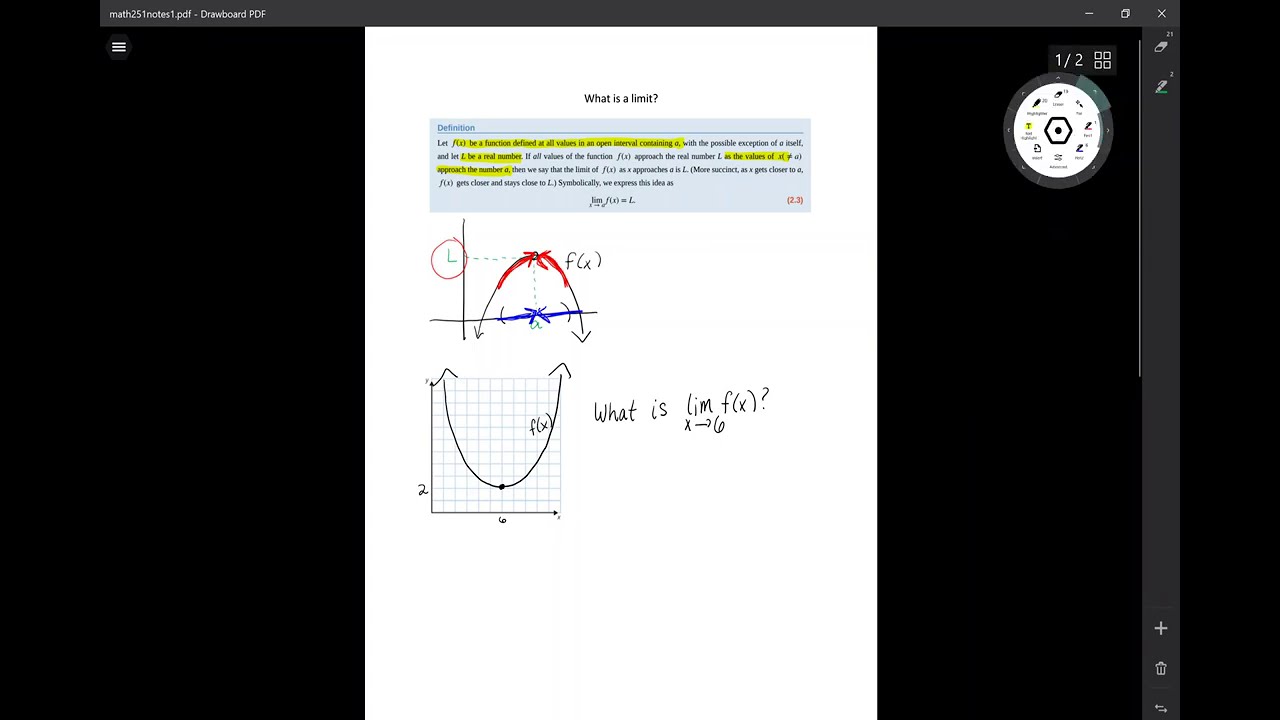
Math 251 - What is a limit?

Limit Kalkulus Part 1: Apa Itu Limit? Penjelasan Mudah & Visual!

Límite de una función real
5.0 / 5 (0 votes)
