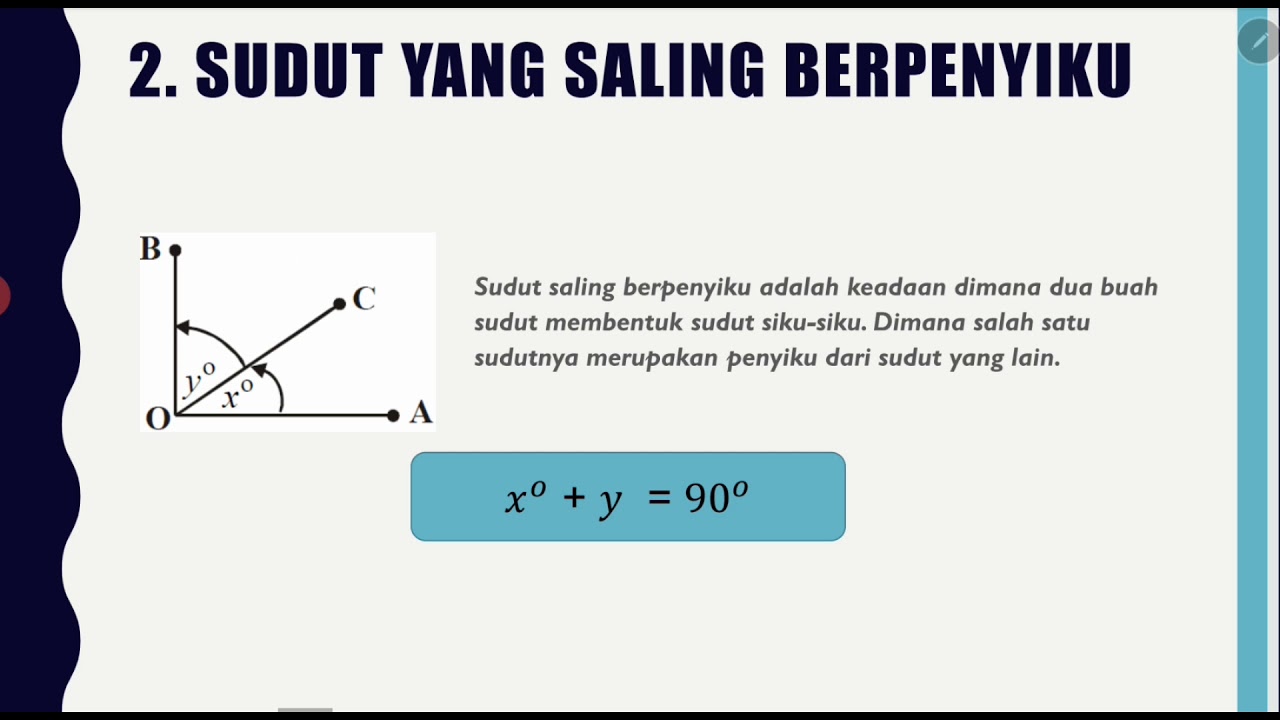
Sudut Berkomplemen atau berppenyiku

Summary

This educational video explains complementary angles, focusing on how two angles add up to 90°. The instructor provides examples, including specific angles like 30° and 60° or algebraic expressions such as 2x, 9x, and 5x + 26°. It covers the process of solving these equations and finding the complementary angles through simple mathematical steps. The video aims to help learners understand and apply the concept of complementary angles in geometry, offering both numerical and variable-based examples for a deeper understanding.

Takeaways

• 😀 Complementary angles are angles that add up to 90°. For example, if one angle is 30°, its complement is 60°.
• 😀 If you know one angle of a complementary pair, you can easily find the other angle by subtracting from 90°.
• 😀 An example is given where the angles 30° and 60° add up to 90°, making them complementary angles.
• 😀 If one angle is 20°, the complementary angle would be 70°, because 90° - 20° = 70°.
• 😀 When solving for a variable in complementary angles, you can set up equations like 2x = 70° and solve for x.
• 😀 If the equation is 9x = 45°, you can solve for x by dividing both sides, giving x = 5.
• 😀 The relationship between complementary angles is used in several example problems, demonstrating the ease of calculating unknown angles.
• 😀 A problem with a complementary angle pair of 45° and 5x + 26° can be solved by setting up an equation and solving for x.
• 😀 If the sum of two angles equals 90°, they are complementary, and this property is used to find unknown angles in problems.
• 😀 The script encourages viewers to continue learning about complementary angles with enthusiasm, ending with a positive, motivational note.

Q & A

What are complementary angles?

Complementary angles are two angles whose sum equals 90°. For example, if one angle is 30° and another is 60°, they are complementary because 30° + 60° = 90°.

How do you find the complement of a given angle?

To find the complement of a given angle, subtract the given angle from 90°. For example, if the angle is 30°, the complement is 90° - 30° = 60°.

What is the formula used to find the value of x in complementary angle problems?

The formula is based on the equation that the sum of the two complementary angles equals 90°. If one angle is expressed as a variable (like 2x), the equation would be: 2x + known angle = 90°.

In the example where one angle is 2x and the other is 70°, how do you solve for x?

The equation is 2x + 70° = 90°. To solve for x, subtract 70° from both sides: 2x = 90° - 70° = 20°. Then divide by 2: x = 20° ÷ 2 = 10°.

What does it mean when two angles are called 'salng berpenyiku' in the context of complementary angles?

'Salng berpenyiku' refers to angles that are complementary to each other, meaning their sum is 90°. In the example provided, the angles of 30° and 60° are salng berpenyiku.

If the given angle is 45° and the other angle is 9x, how do you find the value of x?

Since the angles are complementary, their sum must be 90°. The equation would be: 45° + 9x = 90°. To solve for x, subtract 45° from both sides: 9x = 90° - 45° = 45°. Then divide by 9: x = 45° ÷ 9 = 5°.

What happens if the equation for complementary angles is more complex, such as 5x + 26°?

If the equation is more complex, like 45° and 5x + 26°, first set up the equation: 45° + (5x + 26°) = 90°. Solve for x by simplifying the equation step-by-step.

Why is it important to ensure that the sum of two angles equals 90° in complementary angle problems?

It is important because the defining characteristic of complementary angles is that their sum must always be 90°. This allows you to set up accurate equations and solve for unknown values correctly.

How can you apply the concept of complementary angles to real-life situations?

Complementary angles are often used in fields such as architecture, engineering, and design, where precise angle measurements are important. For example, in building structures with right angles, complementary angles help in ensuring the correct dimensions and alignment.

What is the significance of using algebra to solve for unknown angles in complementary angle problems?

Using algebra allows you to express the unknown angle as a variable (like x), and then use mathematical operations to solve for it. This is a powerful tool for solving more complex angle-related problems, where direct measurement isn't possible.