Ecuación canónica de la Elipse | Centro (0,0)
Summary
TLDREste video ofrece una introducción detallada a las ecuaciones canónicas de la elipse, con un enfoque en las características fundamentales para identificar una elipse en una ecuación. El instructor explica cómo reconocer una elipse al analizar las ecuaciones y sus elementos, como las letras 'x' y 'y' elevadas al cuadrado y la forma de la ecuación. Además, se profundiza en cómo determinar el eje mayor y menor de la elipse, el valor de 'a' y 'b', y la forma en que la ecuación canónica se relaciona con el gráfico de la elipse. Finalmente, se deja un ejercicio práctico para reforzar el aprendizaje.
Takeaways
- 😀 La elipse tiene dos letras principales en su ecuación, generalmente 'x' y 'y'.
- 😀 Para que una ecuación sea de una elipse, ambas letras deben estar elevadas al cuadrado.
- 😀 Las ecuaciones de la elipse se pueden presentar en diversas formas, pero deben cumplir ciertas características comunes.
- 😀 Las ecuaciones generales de la elipse están igualadas a cero y contienen los términos 'x' al cuadrado y 'y' al cuadrado.
- 😀 Una ecuación canónica de la elipse tiene la forma de dos fracciones sumadas, igualadas a 1.
- 😀 Si una ecuación tiene el centro en (0, 0), las fracciones sólo deben contener 'x' y 'y' al cuadrado.
- 😀 La posición del eje mayor de la elipse se determina observando cuál de los dos números al cuadrado es mayor (ya sea debajo de 'x' o de 'y').
- 😀 La distancia 'a' representa la distancia desde el centro al vértice del eje mayor, mientras que 'b' es la distancia al vértice del eje menor.
- 😀 El valor de 'a' y 'b' se obtiene extrayendo la raíz cuadrada de los números al cuadrado en la ecuación.
- 😀 Aunque las ecuaciones de la elipse pueden variar en formato, siempre se deben cumplir las condiciones de que 'x' y 'y' estén al cuadrado y sean positivas.
- 😀 Es posible que algunas ecuaciones no sean de una elipse si no cumplen con las condiciones básicas, como tener números negativos o no estar al cuadrado.
Q & A
¿Qué característica tiene la ecuación de una elipse?
-Una característica importante de la ecuación de una elipse es que debe contener dos letras (generalmente x e y), ambas elevadas al cuadrado, y debe estar igualada a 1 o a un número positivo en su forma canónica.
¿Cómo podemos identificar si una ecuación representa una elipse?
-Una ecuación representa una elipse si tiene dos términos al cuadrado (como x² y y²), ambos con coeficientes positivos, y los términos deben estar sumados. Además, el exponente de ambas letras debe ser 2.
¿Qué diferencia existe entre las ecuaciones generales y las ecuaciones canónicas de una elipse?
-Las ecuaciones generales de una elipse tienen términos que se igualan a cero y pueden tener coeficientes numéricos diferentes, mientras que las ecuaciones canónicas se igualan a 1 y están en la forma fraccionaria, donde ambos términos están divididos por un número positivo.
¿Qué significa que la ecuación esté en forma canónica?
-Que la ecuación esté en forma canónica significa que está representada como una fracción que suma 1, donde las letras x y y están al cuadrado, con coeficientes positivos y con un centro en (0, 0) en este caso.
¿Cómo se determina la posición del eje mayor de la elipse a partir de la ecuación?
-La posición del eje mayor se determina observando qué término (x² o y²) tiene el valor mayor en la ecuación. Si el término con el número mayor está junto a x², el eje mayor será paralelo al eje x; si está junto a y², será paralelo al eje y.
¿Qué relación existe entre los valores de a y b en la ecuación canónica de una elipse?
-En la ecuación canónica de una elipse, 'a' representa la distancia entre el centro y el vértice en el eje mayor, mientras que 'b' representa la distancia entre el centro y el vértice en el eje menor. Además, 'a' siempre debe ser mayor que 'b'.
¿Cómo se encuentran los valores de a y b a partir de la ecuación canónica?
-Para encontrar los valores de a y b, se extrae la raíz cuadrada de los valores de a² y b² presentes en la ecuación canónica. Estos valores representan las distancias de los vértices desde el centro en sus respectivos ejes.
¿Qué significa que la ecuación esté igualada a 1 en su forma canónica?
-Que la ecuación esté igualada a 1 significa que la elipse ha sido normalizada, lo que permite compararla con otras elipses sin la influencia de los coeficientes. Esta forma facilita el cálculo de sus propiedades geométricas, como el valor de a y b.
¿Cómo reconocer si una ecuación no es una elipse?
-Una ecuación no es una elipse si tiene un término con un exponente diferente de 2, si los términos con x y y no están sumados, o si uno de los términos está elevado a un exponente negativo o tiene un signo opuesto.
¿Qué ocurre si los valores de a y b no tienen raíces cuadradas exactas?
-Si los valores de a² o b² no tienen raíces cuadradas exactas, se pueden expresar como raíces cuadradas o calcular su valor decimal aproximado. Esto no afecta la validez de la ecuación, aunque en algunos casos el valor de b puede ser un número decimal.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

🐘 CÓNICAS: Ecuación General RESUMEN 💥Fácil y Rápido💥 #GeometríaAnalítica

63. Encontrar a todos los elementos de una elipse cuando te dan su ecuación general.

HALLAR LA EXCENTRICIDAD Y LA ECUACIÓN DE UNA ELIPSE

Geometría Analítica: Ecuación de la elipse dados foco y la excentricidad.

¿Qué y Cuáles son las secciones Cónicas?
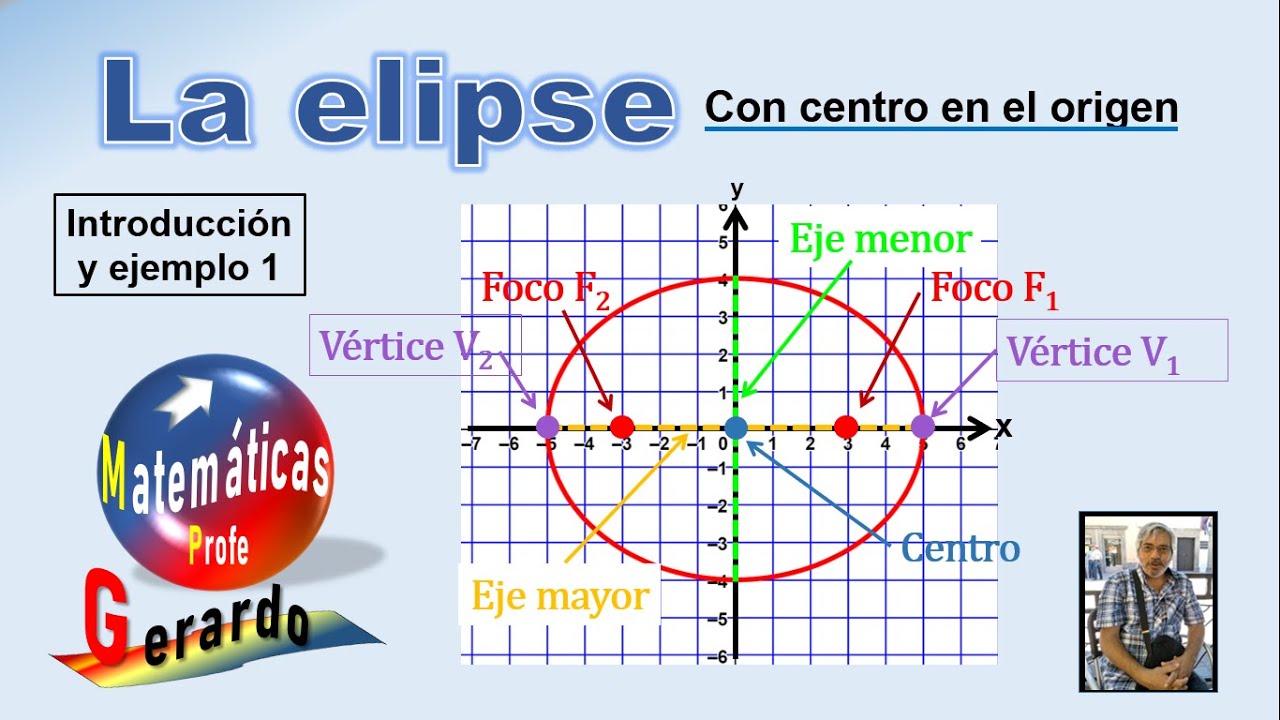
La elipse con centro en el origen. Introducción y ejemplo 1.
5.0 / 5 (0 votes)
