Kelas VIII - Luas Permukaan Limas

Summary

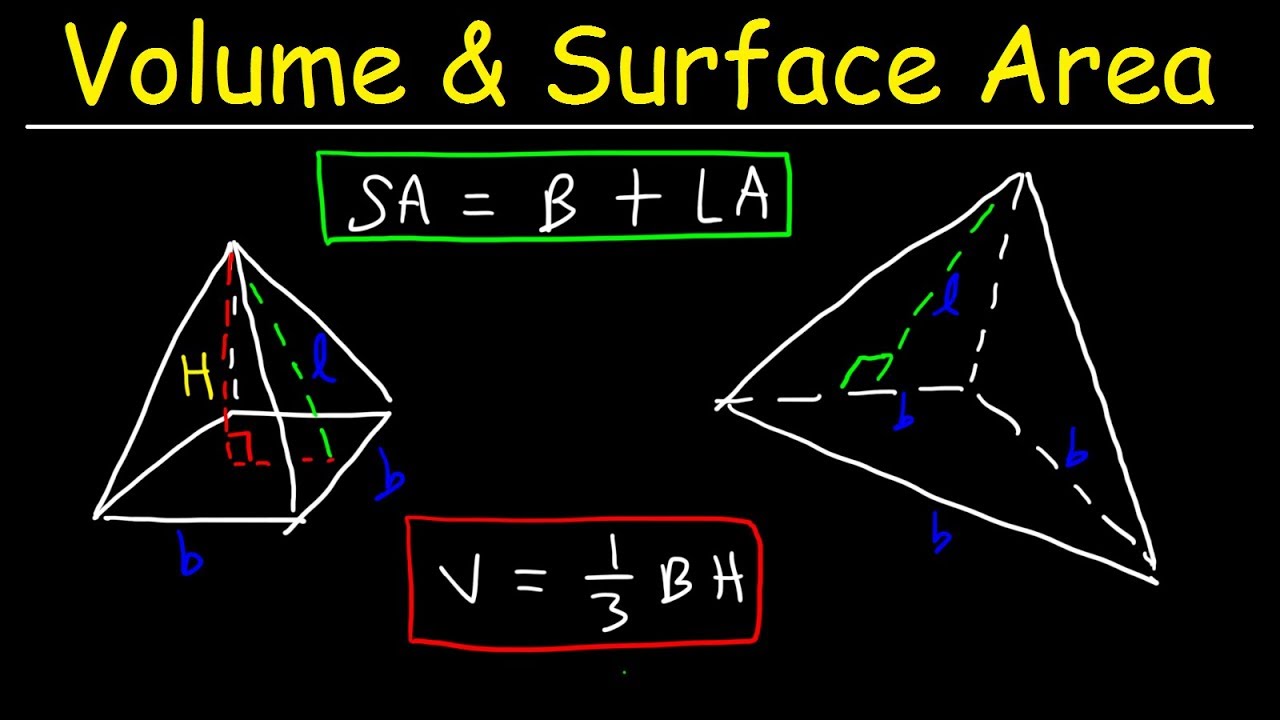
This educational video explains the surface area of pyramids, focusing on various types of pyramids such as square-based, triangular, and regular pyramids. The video breaks down key concepts like the pyramid's base, slant height, and lateral faces. It explains the relationship between the slant height, base side, and the height of the pyramid using the Pythagorean theorem. Through examples, the video demonstrates how to calculate the surface area by adding the area of the base and the lateral faces. The explanation is followed by practical exercises to reinforce the understanding of these calculations.

Takeaways

• 😀 Understanding the components of a pyramid is crucial, including the base (alas), slant faces (sisi tegak), and the height of the pyramid (tinggi limas).
• 😀 The base of the pyramid determines its type: square pyramid for a square base, triangular pyramid for a triangular base, and so on.
• 😀 The height of the pyramid is the perpendicular distance from the apex to the center of the base (tinggi limas).
• 😀 The slant height (tinggi sisi tegak) is the height of the triangular faces surrounding the pyramid and is important for calculating the area of slant faces.
• 😀 The formula for surface area of a pyramid is: Surface Area = Area of the Base + Total Area of the Slant Faces.
• 😀 The area of the base varies depending on the shape of the base (e.g., square, triangle). For a square base, it is calculated as side^2.
• 😀 The area of each slant face is calculated using the formula for the area of a triangle: (1/2) * base * height.
• 😀 The Pythagorean theorem is used to calculate the slant height (tinggi sisi tegak) when the height of the pyramid and half the base length are known.
• 😀 In problems where the base is a square, the areas of all slant faces are the same, allowing the calculation of the total slant face area by multiplying the area of one slant face by 4.
• 😀 Examples illustrate how to apply the formulas in real problems, such as calculating surface area using known dimensions like base side length, slant height, and pyramid height.

Q & A

What is the importance of the base in a pyramid?

The base of a pyramid is crucial because it determines the type and naming of the pyramid. For example, if the base is a square, the pyramid is called a square pyramid, and similarly for other shapes like triangles or pentagons.

What is the definition of a slant height in a pyramid?

The slant height refers to the height of the triangular face of a pyramid, measured along the slant of the side. This should not be confused with the perpendicular height of the pyramid.

How do you calculate the surface area of a pyramid?

To calculate the surface area of a pyramid, you sum the area of the base and the areas of all the triangular faces (lateral surface area). The formula is: Surface Area = Area of Base + Lateral Surface Area.

What is the difference between the height of a pyramid and the height of a triangular face?

The height of a pyramid refers to the perpendicular distance from the apex to the center of the base. The height of a triangular face (slant height) is the distance from the apex to the base of the triangle along the slant of the face.

How do you use the Pythagorean theorem to find the height of a triangular face in a pyramid?

The Pythagorean theorem can be used to find the height of the triangular face by applying it to the right triangle formed by the height of the pyramid, half of the base edge, and the slant height. The formula is: height of the triangular face = √(height of the pyramid² + (half of the base edge)²).

What is the role of the diagonal intersection point in calculating the height of a pyramid?

The intersection point of the diagonals of the base is used to define the center of the base, and it plays a key role in determining the height of the pyramid. The height is measured from the apex to this point.

How is the lateral surface area of a pyramid calculated?

The lateral surface area is the sum of the areas of all the triangular faces. For a pyramid with a square base, the lateral surface area can be calculated by multiplying the area of one triangular face by the number of triangular faces (e.g., 4 for a square base).

What is the relationship between the side length of the base and the area of the triangular faces in a pyramid?

In a pyramid with a square base, the side length of the base determines the base of the triangular faces. The area of each triangular face can be found by using the formula: Area of triangle = ½ × base × height of the triangle.

In the example where the pyramid has a square base with a side length of 12 cm and a slant height of 18 cm, how do you calculate the surface area?

The surface area is calculated by first finding the area of the base (12 cm × 12 cm = 144 cm²) and the area of the triangular faces (each triangle has an area of ½ × 12 cm × 18 cm = 108 cm²). Since there are 4 triangular faces, the total area of the lateral surface is 4 × 108 cm² = 432 cm². The total surface area is 144 cm² + 432 cm² = 576 cm².

What happens when the base of the pyramid is not a square, for example, in a regular pyramid with a pentagonal base?

If the base is not a square, the same method of calculating the surface area applies. You calculate the area of the base based on its shape and then calculate the area of the triangular faces, ensuring you adjust for the number of sides in the base.