ATPL General Navigation - Class 4: Convergency.
Summary
TLDRDieses Video erklärt das Konzept des Great Circles, die kürzeste Verbindung zwischen zwei Punkten auf der Erde, deren Richtung ständig verändert. Es zeigt, wie man die Richtungsänderung misst und zwischen Great Circle und Run Line umschaltet. Der Great Circle verändert sich, weil die relative Position des Nordens sich ändert. Die Konvergenz, die die Differenz zwischen Run Line und Great Circle darstellt, wird durch die Sinusfunktion der Breite und dem Längenwechsel berechnet. Das Video bietet auch Beispiele zur Anwendung dieser Theorie.
Takeaways
- 🌐 Eine Großkreisbahn ist die kürzeste Distanz zwischen zwei Punkten auf der Erde, deren Richtung jedoch ständig verändert.
- 🧭 Die Richtung einer Großkreisbahn ändert sich, weil sie stets auf dem kürzesten Weg zwischen zwei Punkten verläuft und die relative Position des Nordens sich ändert.
- 📐 Die Konvergenz der Längengrade beeinflusst die Veränderung der Großkreisrichtung und hängt von der Nähe zu den Polen ab.
- 🌍 Es gibt keine Konvergenz an der Aequatorlinie, da dort die Längengrade parallel sind, im Gegensatz zu den Polen, wo sie sich zu einem Punkt zusammenschrumpfen.
- 📈 Die Konvergenz der Längengrade kann mit der Sinusfunktion der Breite bestimmt werden, die von 0 bei 0° Breite bis 1 bei 90° Breite ansteigt.
- 📈 Die Formel für die Konvergenz ist 'Sinus der Breite mal dem Veränderung in Längengrad', was die Veränderung der Großkreisrichtung beschreibt.
- 🛫 Um die neue Großkreisrichtung zu bestimmen, addiert man die Konvergenz zur ursprünglichen Richtung, was die neue Richtung am nächsten Punkt gibt.
- 🔄 Der Durchschnitt der Großkreisrichtung entspricht der Rum-Linie, die stets näher an der Aequatorlinie liegt als die Großkreisbahn.
- 🔄 Die Rum-Linie verläuft auf einer konstanten Richtung zwischen zwei Punkten, während die Großkreisbahn ständig verändert.
- 🔢 Der Umschlagswinkel, der die Differenz zwischen Rum-Linie und Großkreis ist, beträgt 0,5 der Konvergenz.
- 📊 Die höchste Breite oder der Scheitelpunkt der Großkreisbahn erreicht, wenn die Großkreisrichtung 90 oder 270 Grad ist, also rein östlich oder westlich verläuft.
Q & A
Was ist ein Großkreis?
-Ein Großkreis ist die kürzeste mögliche Distanz zwischen zwei Punkten auf der Erde, dessen Richtung jedoch ständig verändert.
Was bedeutet es, dass die Richtung eines Großkreises ständig verändert?
-Die Richtung verändert sich, weil man ständig auf den Nordpol bezogen navigiert und die relative Position des Nordpols sich ändert, je nachdem, wo man sich auf der Erde befindet.
Wie wird die Veränderung der Richtung eines Großkreises gemessen?
-Die Veränderung der Richtung wird durch die Konvergenz der Längengrade gemessen, die von der Äquator bis zum Pole zunehmend größer wird.
Was ist die Konvergenz?
-Die Konvergenz ist die Veränderung der Richtung, die aufgrund der Kurven der Längengrade entsteht und von der Breite abhängt, auf der man sich befindet.
Welche mathematische Funktion wird verwendet, um die Konvergenz zu berechnen?
-Die Sinusfunktion wird verwendet, um die Konvergenz basierend auf der Breite und dem Wechsel der Länge zu berechnen.
Was ist der Durchschnittsgroßkreisweg und wie wird er berechnet?
-Der Durchschnittsgroßkreisweg ist die mittlere Richtung des Großkreises zwischen zwei Punkten und wird durch die Hälfte der Summe der Großkreiswege an den beiden Punkten berechnet.
Was ist der Unterschied zwischen einem Großkreisweg und einem Lotweg?
-Der Großkreisweg ist ständig veränderlich, während der Lotweg eine konstante Richtung von Punkt A nach Punkt B hat, die dem Längengrad folgt.
Wo ist die Konvergenz am stärksten?
-Die Konvergenz ist am stärksten an den Polen, wo die Längengrade auf einem Punkt konvergieren und die Veränderung der Richtung gleich dem Wechsel der Länge ist.
Wo ist die Konvergenz am schwächsten?
-Die Konvergenz ist am schwächsten an der Äquator, wo die Längengrade parallel sind und daher keine Richtungsveränderung aufgrund der Konvergenz entsteht.
Was ist der Konversionswinkel und wie wird er berechnet?
-Der Konversionswinkel ist der Unterschied zwischen dem Lotweg und dem Großkreisweg und wird als halbe Konvergenz berechnet.
Wie kann man den Großkreisweg von einem Punkt zu einem anderen bestimmen?
-Man kann den Großkreisweg bestimmen, indem man die Konvergenz berechnet und diese zur Bestimmung der Richtung des Lotwegs hinzufügt, um den Großkreisweg zu erhalten.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Wie Strom zum Magnet wird | Elektromagnetismus

Betrag von Vektoren - Die Länge von Pfeilen | Geraden und Ebenen | Flip the Classroom

Physik 10 / Video 3.2: Addition von Kräften

Grundlagen VEKTOREN – Einstieg Vektorgeometrie einfach erklärt

Introductory NMR & MRI: Video 06: Spin echoes, CPMG and T2 relaxation
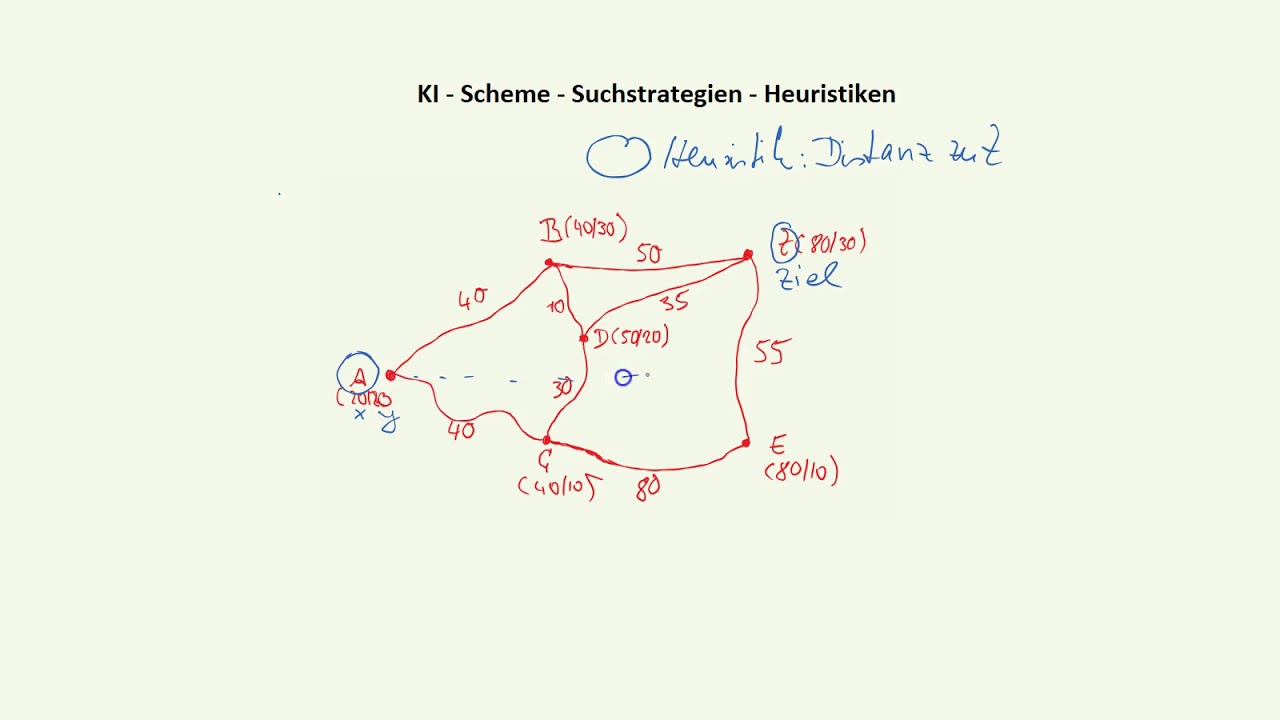
Ki und Scheme - Suchstrategien - Heuristiken

Alpha Centauri - Was ist Entropie - Prof. Harald Lesch
5.0 / 5 (0 votes)