Qué es función | Concepto de función
Summary
TLDREn este video educativo, el instructor introduce los conceptos básicos de las relaciones y las funciones matemáticas. Comienza explicando que una relación es una correspondencia entre elementos de dos conjuntos, ilustrando con ejemplos como la forma de movilizarse de los animales. Luego, define una función como una relación especial que asigna un único valor del segundo conjunto a cada elemento del primer conjunto, demostrando con ejemplos como la suma de 1 y el valor absoluto. El video concluye con ejercicios prácticos para que los estudiantes puedan aplicar y comprender mejor estos conceptos fundamentales de matemáticas.
Takeaways
- 😀 La relación es una correspondencia entre los elementos de dos conjuntos que forman parejas ordenadas.
- 🔍 Un ejemplo de relación se da con el conjunto de animales (pájaro, perro, pez, serpiente) y el conjunto de formas de movilizarse (caminar, volar, nadar).
- 🐟 Los animales tienen diferentes formas de movilizarse; por ejemplo, el pájaro puede caminar y volar, pero no nadar.
- 🚶 La función es una relación especial que une elementos de un conjunto (variable independiente) con elementos de otro conjunto (variable dependiente) de una manera única.
- 📚 Todas las funciones son relaciones, pero no todas las relaciones son funciones.
- 🔢 Se ilustra la definición de función con ejemplos numéricos, como la función que suma 1 a cada número (x + 1).
- 📉 Otros ejemplos de funciones incluyen el valor absoluto de un número, que transforma un número negativo en positivo.
- 🔑 La variable independiente es aquella que no depende de nada, mientras que la variable dependiente es determinada por la función.
- 👉 Se enfatiza que para que una relación sea una función, cada elemento del primer conjunto debe asignar un único elemento del segundo conjunto.
- 📚 Se proporcionan ejercicios para que los estudiantes practiquen y comprendan la diferencia entre relaciones y funciones.
- 📘 Se ofrecen recursos adicionales, como un curso completo de funciones en el canal del instructor o enlaces en la descripción del video.
Q & A
¿Qué es una relación en matemáticas según el script?
-Una relación en matemáticas es una correspondencia entre los elementos de dos conjuntos que forman parejas ordenadas. Es una expresión que une dos o más objetos entre sí.
¿Cómo se relacionan los animales con las formas de movilizarse en el ejemplo dado en el script?
-En el ejemplo, los animales (pájaro, perro, pez, serpiente) se relacionan con las formas de movilizarse (caminar, volar, nadar) de acuerdo a sus capacidades naturales. Por ejemplo, el pájaro puede caminar y volar, pero no nadar.
¿Qué es una función y cómo se diferencia de una relación en el script?
-Una función es una relación especial entre dos conjuntos que asigna a cada valor del primer conjunto (variable independiente) un único valor del segundo conjunto (variable dependiente). Mientras que todas las funciones son relaciones, no todas las relaciones son funciones.
¿Cómo se define la función 'sumarle 1' en el script?
-La función 'sumarle 1' es una relación donde a cada número del conjunto de la variable independiente se le suma 1 para obtener el valor en el conjunto de la variable dependiente. Esto se representa matemáticamente como f(x) = x + 1.
¿Qué es el valor absoluto y cómo se relaciona con la función en el ejemplo del script?
-El valor absoluto de un número es la distancia desde ese número hasta el cero en el eje numérico, siempre resultando en un valor positivo. En el ejemplo del script, la función busca el valor absoluto de cada número, eliminando su signo negativo si lo tiene.
¿Por qué el conjunto de números se llama variable independiente y por qué el otro se llama variable dependiente en el script?
-El conjunto de números se llama variable independiente porque sus valores no dependen de nada más; son los valores que elegimos. Por otro lado, la variable dependiente son los valores que resultan después de aplicar la función, y dependen de los valores de la variable independiente.
¿Cómo se determina si una relación es una función según lo explicado en el script?
-Para que una relación sea una función, debe cumplirse que a cada elemento del primer conjunto (variable independiente) le corresponde exactamente uno y solo uno del segundo conjunto (variable dependiente). No pueden haber elementos que no tengan correspondencia o que tengan múltiples correspondencias.
¿Qué es el ejemplo práctico de relación que no es una función mencionado en el script?
-El ejemplo práctico que no es una función es el de un hombre relacionado con una mujer. Aunque es una relación, no cumple con la definición de función porque no es una relación biunívoca, es decir, no asigna un único elemento del segundo conjunto a cada elemento del primer conjunto.
¿Cuál es el ejercicio propuesto en el script para que los espectadores practiquen la distinción entre relaciones y funciones?
-El ejercicio consiste en dos partes: primero, determinar si la relación del número de lados de figuras geométricas es una función, y segundo, si la relación de multiplicar el número de lados por 2 es una función. En ambos casos, se debe verificar si a cada elemento del primer conjunto le corresponde uno y solo uno del segundo conjunto.
¿Cuál es la conclusión del script sobre las funciones y cómo se relacionan con las relaciones?
-La conclusión del script es que una función es una relación especial que une en parejas ordenadas los elementos de un conjunto con los de otro, asignando a cada elemento del primer conjunto solamente uno del segundo conjunto. Es importante destacar que no todas las relaciones son funciones, solo aquellas que cumplen con la condición de asignar un único elemento del segundo conjunto a cada uno del primero.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Recorrido Matematico: Introduccion a las Funciones y Relaciones

FORMULA MOLECULAR Y ESTRUCTURAL. ISOMEROS. QUIMICA ORGANICA. QUIMICA CON IRWIN

Construcción de una señal a partir de la función rampa y la función escalón unitario Ejemplo # 2

CURSO MATEMÁTICAS DESDE CERO | La mejor forma de iniciar
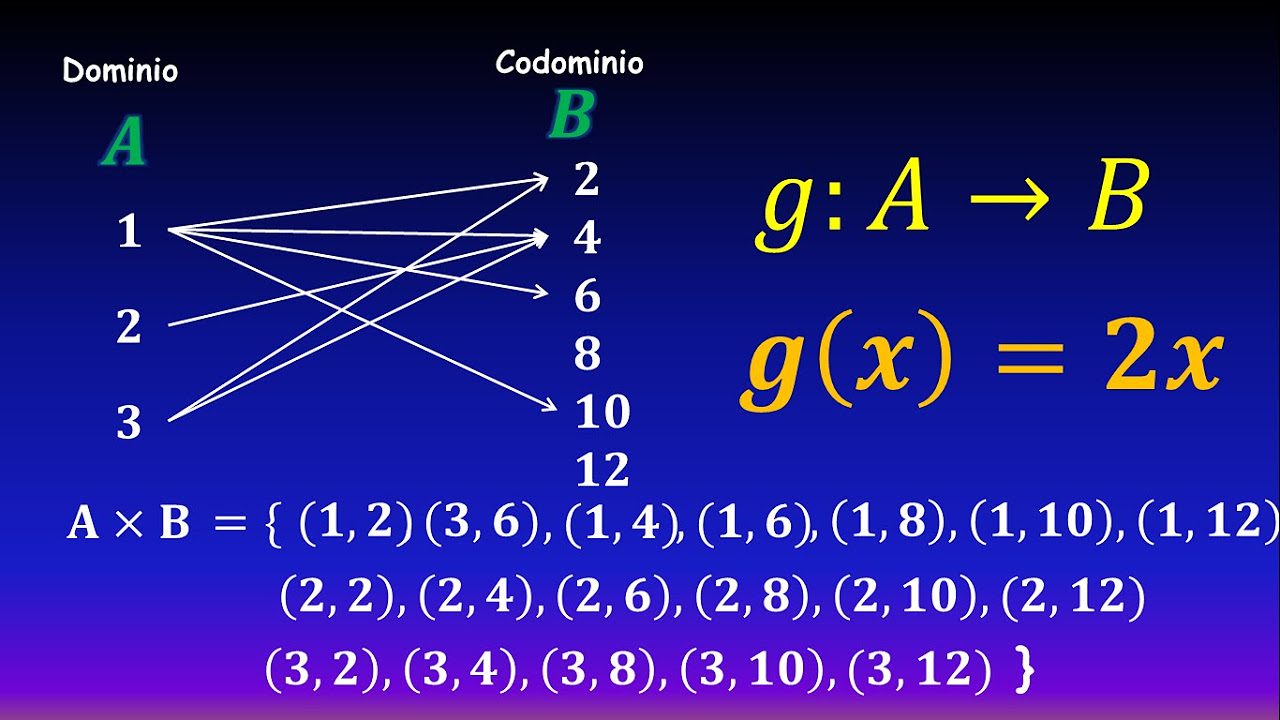
01. ¿Qué es una Función? (Funciones, relaciones, producto cartesiano)

🤗🚀Etapas del APRENDIZAJE MATEMÁTICO en educación INICIAL🥰🥰
5.0 / 5 (0 votes)
