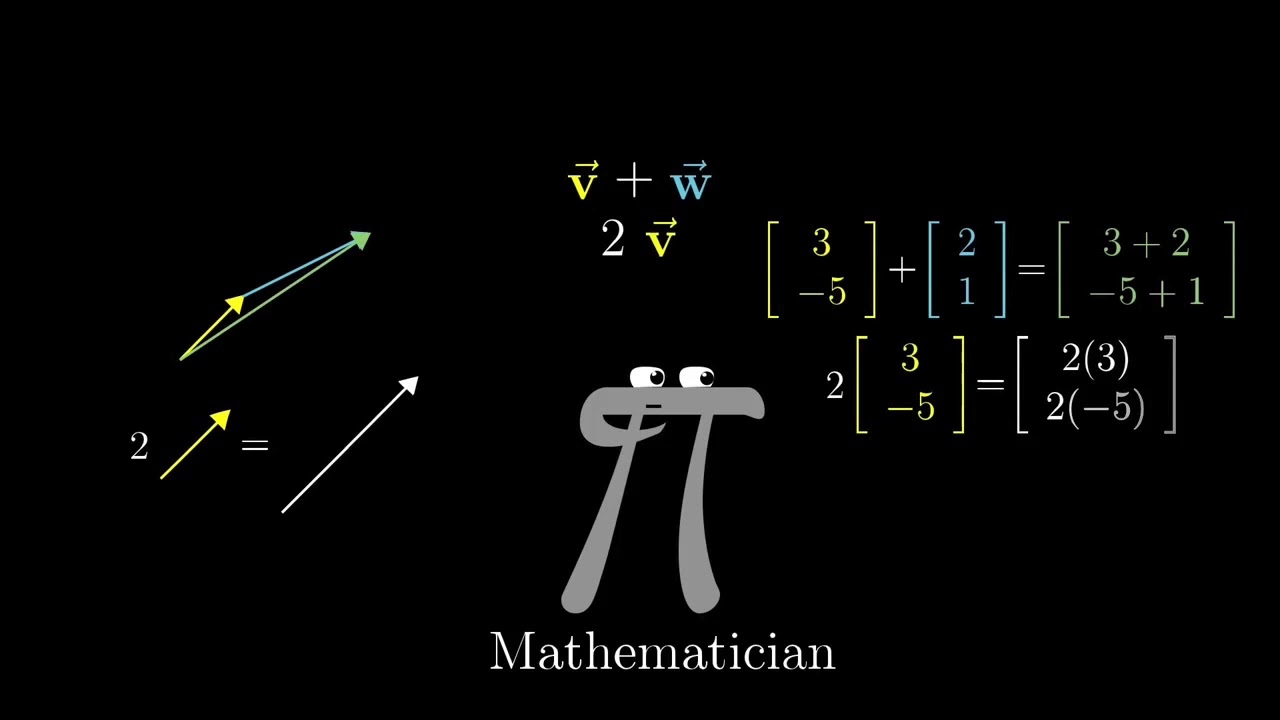M4ML - Linear Algebra - 1.3 Getting a handle on vectors

Summary

This video introduces the fundamental concept of vectors in linear algebra, focusing on their role in optimizing data fitting. Using the example of fitting a Gaussian distribution to a population's height data, the video explains how vectors can represent changes in model parameters (like mean and standard deviation). By minimizing the 'badness' of the fit through vector adjustments, the process leads to better model accuracy. The video also connects vector mathematics to real-world applications in fields like machine learning, data science, and even Einstein's theory of relativity, providing an intuitive foundation for optimization techniques like gradient descent.

Takeaways

• 😀 Vectors are essential in solving linear algebra problems, especially in data fitting tasks.
• 📊 Fitting a function, such as a normal distribution, to data involves finding optimal parameters (μ and σ).
• 🔍 The goal of fitting is to minimize the error or 'badness' of the fit, represented by the sum of squared differences between the predicted and actual values.
• 📉 The goodness of fit can be visualized as a contour map, where we seek the lowest point (optimal parameters).
• 🚶‍♂️ Movements in parameter space (mu and sigma) are treated as vectors, guiding the search for the best fit.
• 📐 Vectors are not just geometric entities; they can represent abstract spaces, such as parameter spaces in data fitting.
• 🔧 Optimization requires understanding how vectors move in these spaces to find the best possible fit.
• 💡 Calculus and vector mathematics work together to help find gradients and minima in optimization tasks.
• ⚙️ The concept of vectors extends beyond geometry and physics, including applications in fields like metallurgy and machine learning.
• 📚 Mastering vectors and calculus is crucial for solving real-world problems in data science, machine learning, and optimization.

Q & A

What is the primary focus of the video on Linear Algebra?

The primary focus is on understanding vectors and how they are used to solve linear algebra problems, particularly in fitting parameters for data distributions, such as the Gaussian distribution.

Why are vectors important in solving linear algebra problems related to data?

Vectors are important because they help in representing changes in parameters, such as the center (mu) and width (sigma) of a distribution, which is critical for fitting data accurately and minimizing error.

What is the histogram distribution of heights used to demonstrate?

The histogram distribution of heights is used to demonstrate how data, such as the population's height distribution, can be modeled using mathematical functions, and how parameters like mu (center) and sigma (width) can fit the distribution.

What is the equation for fitting the height distribution?

The equation for fitting the height distribution is a Gaussian or normal distribution: f(x) = (1 / (sigma * sqrt(2 * pi))) * exp(- (x - mu)^2 / (2 * sigma^2)), where mu is the center, and sigma is the width.

How do we assess the goodness of the fit for the distribution?

The goodness of fit is assessed by calculating the sum of the squared differences between the observed data and the fitted values, and plotting how this goodness varies as the fitting parameters (mu and sigma) change.

What happens if we make a wrong initial guess for mu and sigma in the fit?

If the initial guess for mu and sigma is incorrect, the distribution will be misaligned, resulting in overestimations and underestimations at different parts of the curve, which can be seen in the sum of squared differences.

What is the concept of 'contour maps' in relation to parameter fitting?

Contour maps represent different levels of goodness or badness of fit for various values of mu and sigma. The contours help visualize how changes in parameters affect the quality of the fit and guide optimization towards the best fit.

What is the role of vectors in parameter space optimization?

Vectors in parameter space represent the direction and magnitude of changes in parameters like mu and sigma. By using vectors, we can move in the parameter space to find the optimal values that minimize the goodness function.

How does the concept of vectors extend beyond geometry and into fields like machine learning?

Vectors are not just geometric objects; they can represent any set of parameters or data points, such as the characteristics of a car or the composition of an alloy. This abstraction allows vectors to be used in machine learning and data science for optimization and fitting.

Why is calculus necessary to find the optimal fit in parameter space?

Calculus is necessary to find the optimal fit because it helps in calculating the gradients of the goodness function, guiding us towards the minimum point (optimal parameters). Calculus tools like gradients allow for efficient optimization, especially in machine learning.

What connection does the video make between vectors, calculus, and machine learning?

The video connects vectors and calculus by showing that vectors represent changes in parameter space, and calculus helps optimize those parameters. This understanding is essential for machine learning and data science, where fitting functions to data is a key task.