How To Graph Polynomial Functions Using End Behavior, Multiplicity & Zeros
Summary
TLDRThis video explains how to graph polynomial functions, covering key concepts like end behavior, multiplicity, and finding zeros. The video begins with examples of even and odd polynomials, such as y = x² and y = -x², discussing their symmetrical properties and end behavior. It also delves into the impact of multiplicity on the graph's behavior near x-intercepts, explaining how multiplicity of 1, 2, or 3 influences whether the graph crosses, bounces, or has a horizontal tangent at the x-axis. The video concludes with a step-by-step guide on graphing a specific polynomial and determining its end behavior and intercepts.
Takeaways
- 😀 Even degree polynomials with a positive leading coefficient have an 'up-up' end behavior (both sides of the graph rise towards infinity).
- 😀 Even degree polynomials with a negative leading coefficient have a 'down-down' end behavior (both sides of the graph fall towards negative infinity).
- 😀 Odd degree polynomials with a positive leading coefficient have a 'down-up' end behavior (the graph falls on the left and rises on the right).
- 😀 Odd degree polynomials with a negative leading coefficient have an 'up-down' end behavior (the graph rises on the left and falls on the right).
- 😀 The multiplicity of a zero affects the graph's behavior at the x-intercept: a multiplicity of 1 means the graph crosses the x-axis, multiplicity 2 means the graph bounces off the axis, and multiplicity 3 means it crosses with a horizontal tangent.
- 😀 When graphing polynomials in factored form, find the zeros by setting each factor equal to zero and solving for x.
- 😀 The multiplicity of each factor is determined by its exponent. A higher multiplicity means the graph's behavior at that zero becomes more 'flattened'.
- 😀 To graph polynomials, first identify the x-intercepts (zeros) and their multiplicities, then use the degree and leading coefficient to determine the end behavior.
- 😀 The end behavior of a polynomial function is largely determined by its degree (even or odd) and the sign of the leading coefficient.
- 😀 Symmetry in polynomial graphs occurs when factors have the same multiplicity, especially for polynomials with even degrees.
Q & A
What is the main topic of this video?
-The video discusses how to graph polynomial functions using key concepts such as end behavior, multiplicity, and finding the zeros of the function.
What is end behavior in polynomial functions?
-End behavior refers to the behavior of the graph as x approaches positive or negative infinity. It helps determine whether the graph goes up or down on either end based on the degree and leading coefficient of the polynomial.
How do you describe the end behavior of y = x²?
-For y = x², which is an even function with a positive leading coefficient, the end behavior is 'up' on both sides. As x approaches positive or negative infinity, y approaches positive infinity.
What happens to the graph of y = -x² compared to y = x²?
-The graph of y = -x² is a reflection of y = x² over the x-axis because of the negative leading coefficient. As a result, the end behavior for y = -x² is 'down' on both sides, with y approaching negative infinity as x approaches positive or negative infinity.
What is the end behavior of the graph of y = x³?
-For y = x³, the graph has an odd degree with a positive leading coefficient, so the end behavior is 'down' on the left and 'up' on the right.
What is the end behavior for y = -x³?
-For y = -x³, with an odd degree and a negative leading coefficient, the end behavior is 'up' on the left and 'down' on the right.
What determines the end behavior for polynomials with even degrees?
-For polynomials with even degrees, the end behavior is either 'up' on both sides or 'down' on both sides. The direction depends on whether the leading coefficient is positive (up-up) or negative (down-down).
How do odd-degree polynomials behave in terms of end behavior?
-Odd-degree polynomials alternate in end behavior: if the leading coefficient is positive, the graph goes 'down' on the left and 'up' on the right; if the leading coefficient is negative, the graph goes 'up' on the left and 'down' on the right.
What does the multiplicity of a zero affect in a polynomial graph?
-The multiplicity of a zero determines how the graph behaves near the x-intercept. If the multiplicity is 1, the graph crosses the x-axis in a straight line. If the multiplicity is 2, the graph bounces off the x-axis. If the multiplicity is 3, the graph crosses the x-axis with a horizontal tangent.
How do you find the zeros of a polynomial given in factored form, like y = (x + 2)(x - 1)²(x - 4)?
-To find the zeros of a polynomial in factored form, set each factor equal to zero and solve for x. In this example, the zeros are x = -2, x = 1, and x = 4.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Fundamental Theorem of Algebra
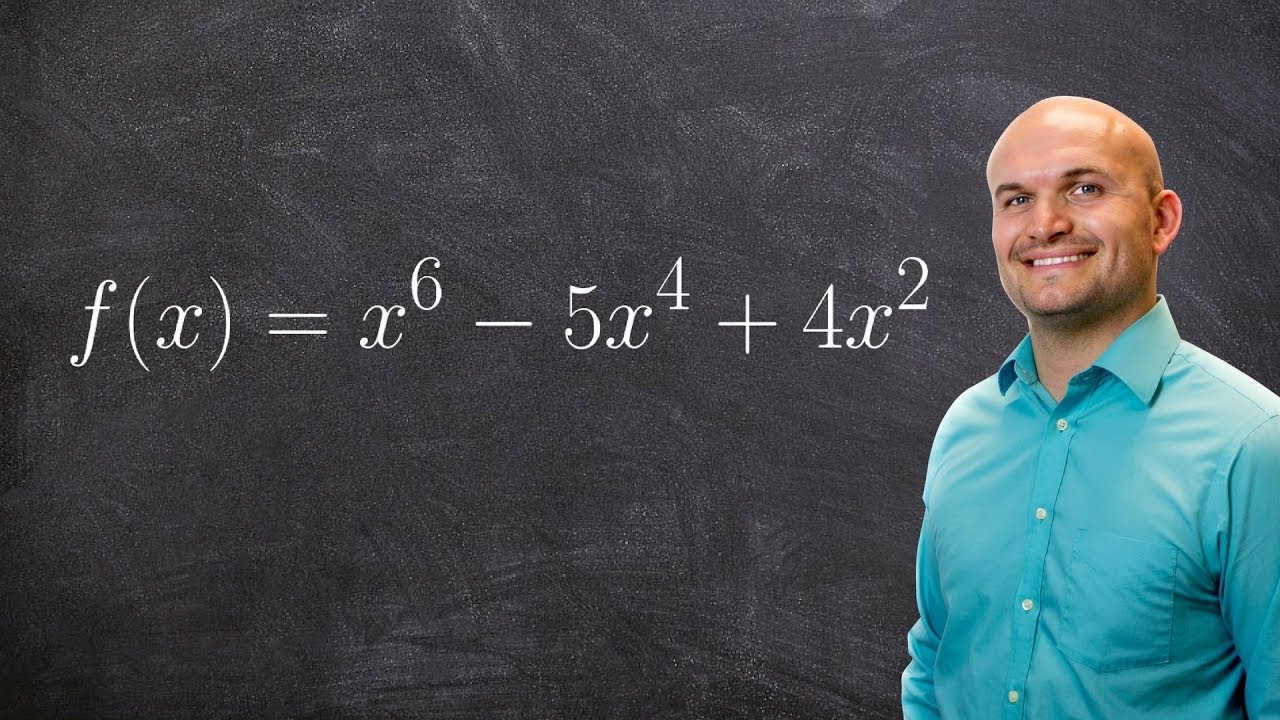
How do we find multiplicity and use it to graph a polynomial

Multiplicity of zeros of polynomials | Polynomial graphs | Algebra 2 | Khan Academy

Grade 10 - Illustrating and graphing polynomial functions | SirABC

AP Precalculus – 1.6 End Behavior and Polynomial Functions
Polynomial Functions - Polynomial Function or NOT? Grade 10 Math Second Quarter
5.0 / 5 (0 votes)
