Newton’s Method | Numerical Methods
Summary
TLDRThis video introduces Newton's Method, an open root-finding technique for non-linear functions. The method begins with an initial guess and iteratively refines the estimate using a first-order Taylor series approximation. By finding the tangent’s intersection with the x-axis, Newton's Method approximates the root of a function. The video explores the method's procedure, highlighting its speed and efficiency, while also discussing potential pitfalls like divergence, especially in step-like functions. The video focuses on the theory behind the method, with a follow-up planned to demonstrate practical applications in future videos.
Takeaways
- 😀 Newton’s Method is an open root-finding technique for non-linear functions, where we iteratively solve for the root starting from an initial guess.
- 😀 The method relies on Taylor series expansion, which allows continuous functions to be approximated as polynomials, making derivatives easier to calculate.
- 😀 In Newton’s Method, we start with an initial guess for the root and use a first-order Taylor series approximation to move toward the solution.
- 😀 The next step in the process involves calculating the derivative at the initial guess to find the instantaneous rate of change of the function.
- 😀 The method involves finding where the tangent line of the derivative hits the x-axis, allowing us to solve for the input that gives an output of zero.
- 😀 By setting the function to zero and solving for the input, we derive the equation that forms the basis of Newton’s Method.
- 😀 After finding the tangent’s intersection with the x-axis, we use the new x-value to calculate the next approximation in the iterative process.
- 😀 This iterative process continues until the difference between successive approximations is small enough, indicating an acceptable error threshold.
- 😀 Newton’s Method is generally faster than closed root-finding methods, but there is no guarantee it will converge to the correct root.
- 😀 Potential failures of Newton’s Method can occur with functions that have step-like behavior or poorly-behaved derivatives, causing divergence or incorrect results.
- 😀 The next video will cover practical applications of Newton’s Method, including solving problems by hand and using programming languages.
Q & A
What is Newton's method and what type of problems does it solve?
-Newton's method is an open root-finding algorithm used to find the roots of nonlinear functions. It starts with an initial guess for the root and iteratively refines the estimate using derivatives to converge to the actual root.
What is the role of the Taylor series expansion in Newton's method?
-The Taylor series expansion is used in Newton's method to approximate a function as a polynomial. This helps in simplifying the computation of derivatives, which are crucial for the iterative process of finding the root.
What does the first-order Taylor series approximation look like in Newton's method?
-The first-order Taylor series approximation involves using the function's value and its derivative at a given point to estimate the function's behavior near that point. The formula is: f(x) ≈ f(x₀) + f'(x₀)(x - x₀), where x₀ is the initial guess.
Why is the derivative important in Newton's method?
-The derivative is crucial because it provides the instantaneous rate of change of the function at a point, which is used to calculate the slope of the tangent line. This tangent is then used to find the next approximation of the root.
How is the next approximation for the root determined in Newton's method?
-The next approximation is determined by finding the x-value where the tangent of the current point intersects the x-axis. This is done by solving the equation f(x) = 0 using the first-order Taylor series approximation.
What does the equation derived from the Taylor series approximation represent in Newton's method?
-The equation derived from the Taylor series approximation represents the input x-value that results in the tangent line crossing the x-axis, i.e., the root of the function. It is the foundation for updating guesses iteratively in Newton's method.
What happens after each iteration in Newton's method?
-After each iteration, the new approximation for the root is plugged into the function to find the output. This process is repeated until the approximation is close enough to the true root, based on a defined acceptable error margin.
What are the advantages of Newton's method?
-Newton's method is typically very fast at finding roots, often requiring fewer iterations than other methods, especially when the function behaves smoothly and the initial guess is close to the true root.
What are some limitations or potential pitfalls of Newton's method?
-Newton's method can fail if the function has a step-like behavior, or if the initial guess is far from the true root. In such cases, the method may diverge or produce inaccurate results.
What kind of functions could cause Newton's method to fail?
-Functions with discontinuities or points where the derivative is zero can cause Newton's method to fail. For example, step functions or functions with sharp turns may lead to divergence, making the method ineffective.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Bisection Method | Numerical Methods

Fixed Point Iteration Method Intuition | Numerical Methods
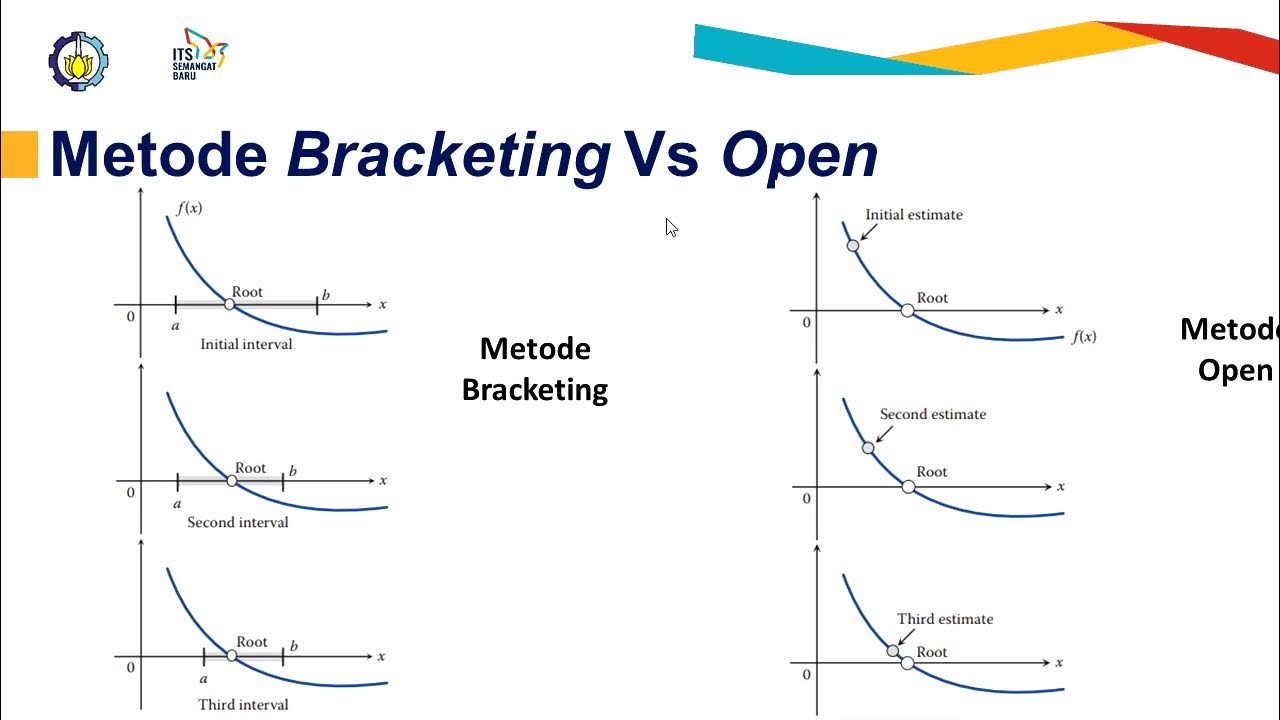
Fisika Komputasi 1: Metode-metode Akar persamaan Secara Numerik

METODE NUMERIK P7 PART 1/2 | METODE NEWTON-RAPHSON UNTUK MENYELESAIKAN PERSAMAAN NON LINIER

Zeros de funções Método Iterativo Linear
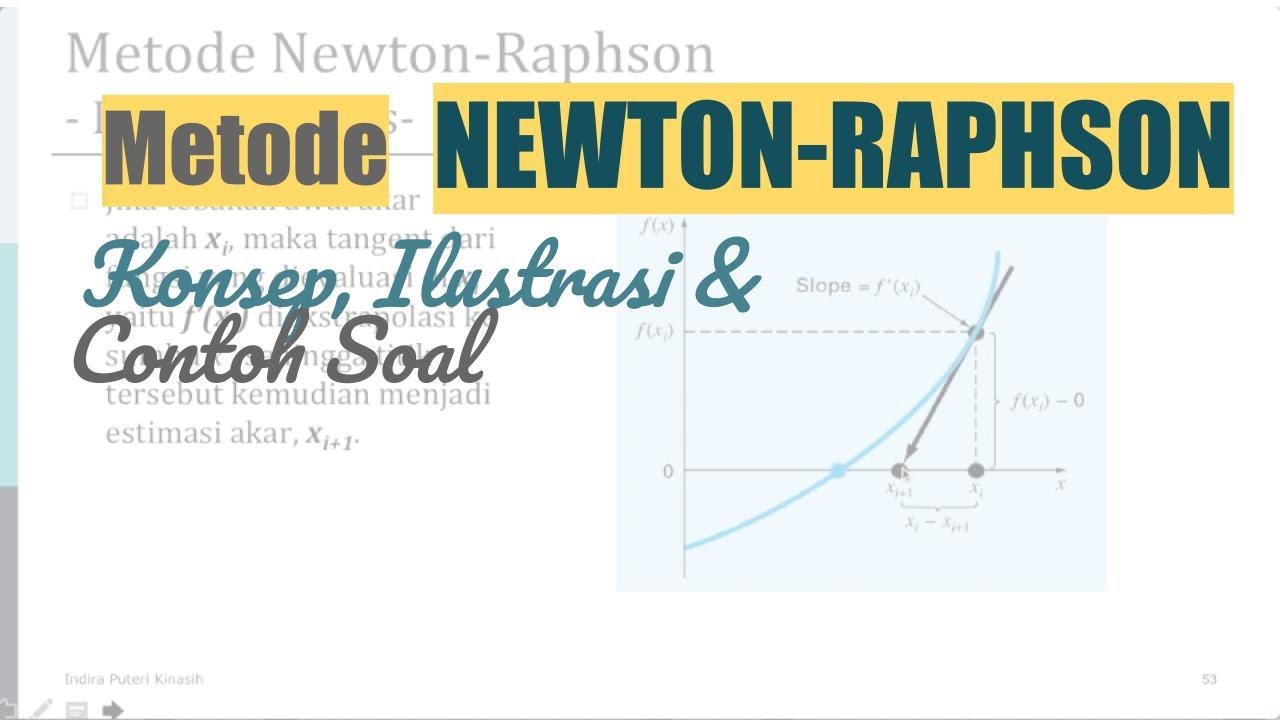
Metode Newton Raphson (Konsep & Contoh) [Metode Numerik]
5.0 / 5 (0 votes)
