Double and Triple Integrals
Summary
TLDRThis tutorial delves into the concept of double and triple integrals, expanding on their use to calculate areas and volumes in multiple dimensions. It covers the process of performing double integrals over both rectangular and curved regions, demonstrating how to set and adjust bounds. The video explains how to handle integration when the region of interest is defined by curves, offering strategies for selecting the most efficient order of integration. Finally, the tutorial touches on triple integrals, showing how the same principles apply to higher-dimensional problems. A valuable resource for understanding advanced integration techniques in calculus.
Takeaways
- 😀 Double integrals help calculate the volume under a surface defined by a function f(x, y).
- 😀 The order of integration can be swapped, but it's crucial to adjust the bounds accordingly.
- 😀 For rectangular regions, double integrals are straightforward, with integration performed step-by-step.
- 😀 Curved regions complicate integration, requiring careful handling of the bounds and variables.
- 😀 Intersections of curves define the boundaries for integration when dealing with curved regions.
- 😀 When integrating over x first, the bounds for y are expressed as functions of x, and vice versa.
- 😀 Choosing the order of integration can make the computation easier, especially when avoiding complex expressions like square roots.
- 😀 Triple integrals extend the concept of double integrals, adding a third dimension to the process.
- 😀 The process of triple integration follows the same rules as double integration, but with an additional variable and more complex bounds.
- 😀 Negative volume values in integrals indicate that the surface lies below the xy-plane, which is useful for interpreting physical scenarios.
- 😀 Multiple integrals are widely used in various fields of math and science, making understanding their setup and execution essential.
Q & A
What is the purpose of double integrals in calculus?
-Double integrals are used to calculate the volume beneath a surface defined by a function of two variables (x, y). It extends the concept of finding the area beneath a curve to higher dimensions.
What does the order of integration in double integrals depend on?
-The order of integration in double integrals depends on the bounds of the region being integrated over. As long as the proper tracking of variables and their bounds is maintained, the order can be changed to simplify the calculation.
How do we perform the integration when the bounds depend on variables?
-When the bounds depend on variables, it’s essential to properly express the limits for each variable in relation to the other variables, and adjust the bounds accordingly when changing the order of integration.
What is the difference between integrating over a rectangular region and a region defined by curves?
-When integrating over a rectangular region, the bounds are constant values. However, for regions defined by curves, the bounds are determined by the intersections or relationships between the curves, which must be carefully expressed in terms of the variables.
How do we find the points of intersection of curves like y = x² and y = 2x?
-To find the points of intersection, set the two equations equal to each other (x² = 2x) and solve for x. This results in x = 0 and x = 2. These values can then be substituted into the original equations to find the corresponding y-values.
Why do we need to be careful when choosing integration bounds for regions between curves?
-It’s important to choose the correct bounds because the lower bound should correspond to the lower curve, and the upper bound should correspond to the higher curve. Using incorrect bounds can lead to errors in the calculation, especially in terms of sign.
What happens when the surface being integrated is below the xy-plane?
-If the surface is below the xy-plane, the result of the integral will be negative, indicating that most of the volume lies below the plane.
What is the significance of triple integrals in higher dimensions?
-Triple integrals extend the concept of multiple integrals to three dimensions, calculating 'hypervolumes' in four-dimensional space. Each subsequent integral eliminates a variable, and the process remains similar to double integrals, but with an added dimension.
What should you remember when setting up triple integrals?
-When setting up triple integrals, remember the order of integration and ensure that each bound depends on the correct remaining variables. As you integrate each variable, you eliminate it from the bounds of the remaining integrals.
How can you simplify triple integrals when dealing with complex functions and boundaries?
-Choosing the appropriate order of integration based on the complexity of the integrand and bounds can simplify the calculation. For example, avoiding complex square roots or negative values can make the process easier to handle.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
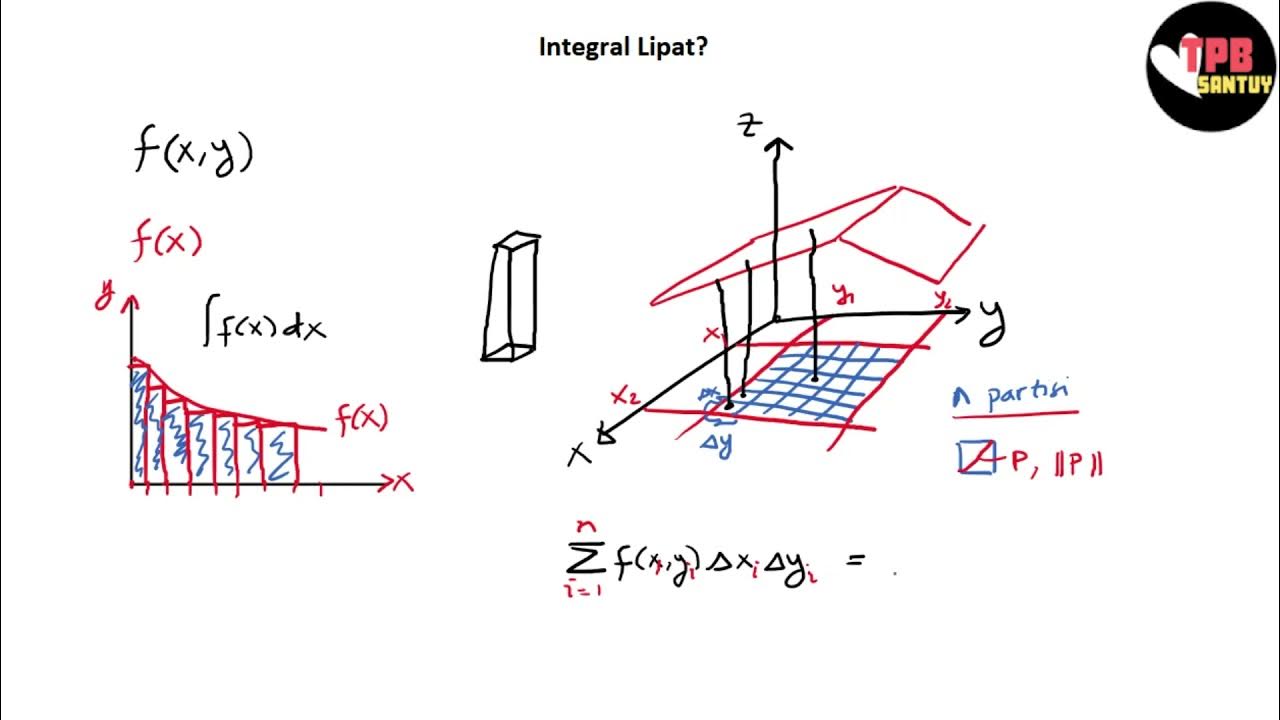
Integral Lipat | Integral Lipat (Part 1) | Kalkulus

Matematika Dasar II | Integral Lipat Dua pada Persegi Panjang

¿Qué es la INTEGRAL? | SIGNIFICADO de la integral definida (Lo que no te enseñan sobre la integral)
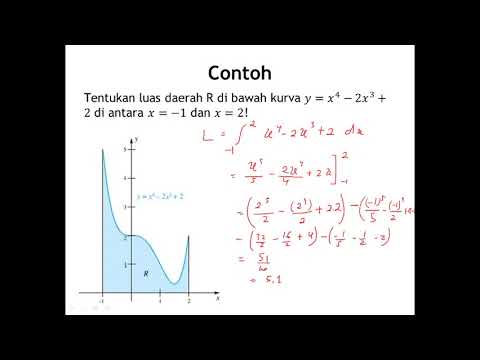
5 1 Luas Daerah Bidang Rata

Kuliah Asinkron Matematika 2

What is Double integral? Triple integrals? Line & Surface integral? Volume integral? #SoME2
5.0 / 5 (0 votes)
