Integral de una raíz | Ejemplo 2
Summary
TLDR在本视频中,讲解者继续探讨含有根号的积分,重点介绍如何处理包含代数单项式的根号。首先,讲解者通过回顾前一个视频中的步骤,展示如何将根号表达为指数形式,接着讲解如何利用根号的性质将根号分离并求解积分。过程中包括了如何处理常数的提取、如何通过增指数法进行积分,以及如何整合积分结果。最后,讲解者提供了一个练习题,鼓励观众自行练习并与解答进行对比。
Takeaways
- 😀 在这个视频中,我们将继续练习带有根号的积分,但只讨论包含代数单项式的情况。
- 😀 本视频中,只涉及代数单项式的根号,不涉及对数、指数或其他类型的表达式。
- 😀 在处理根号时,首先将其转化为幂的形式以便积分,这是之前视频中讲解的方法。
- 😀 通过利用根号的性质,可以将根号内的乘法分开,例子中是将根号3x分开为根号3和根号x。
- 😀 常数项(如根号3)可以从积分中提取出来,简化计算过程。
- 😀 积分操作中,需要将根号x转化为x的幂形式,x的1/2次方,再进行积分。
- 😀 积分过程包括将指数加1,之后除以新的指数值。
- 😀 永远不要忘记在积分结果中加上常数项C,这是积分的基本要求。
- 😀 完成操作后,常数项和结果可以合并简化,最终得到一个更简洁的表达式。
- 😀 视频结尾提供了一个类似的练习题,鼓励观众暂停视频并练习,最后对照答案。
- 😀 视频内容简洁但有效,适合需要巩固根号积分方法的学生,并建议观看更多相关视频。
Q & A
在这个视频中,我们主要讨论了哪种类型的积分?
-我们主要讨论了包含代数单项式的平方根的积分,没有涉及对数或指数等其他类型的积分。
如何处理一个含有平方根的代数单项式的积分?
-首先,我们将平方根转化为指数形式,然后根据积分的规则进行计算,注意在处理时可以利用平方根的分离性质。
如何处理积的平方根?
-当遇到积的平方根时,我们可以将平方根分开,分别计算每个部分的积分。例如,√(3 * x) 可以写作 √3 * √x,√3 是常数,可以提到积分符号外。
如何处理常数项?
-常数项可以从积分中提到外面,这样简化计算。例如,积分中含有常数 3 时,可以把它提取到积分外。
在积分过程中,如何处理平方根的指数形式?
-平方根的指数形式是 x^(1/2),在积分时我们需要加上 1,使指数变为 3/2,然后进行常规的积分计算。
为什么要在积分结果中加上常数项 C?
-常数项 C 是不定积分的标准做法,表示所有可能的原函数的差异。
如何简化积分结果中的表达式?
-在得到积分结果后,通常会进行化简。比如,分母中有平方根时,可以将其转化为指数形式,或者通过代数简化进一步简化答案。
视频中提到的 `x^(1/2)` 的积分是怎样进行的?
-对于 x^(1/2),我们将指数加 1,得到 3/2,然后积分公式是 x^(3/2) 除以 3/2,最终得到 x^(3/2) * 2/3。
如何处理平方根与常数的乘积?
-平方根与常数的乘积可以分开处理,将常数提到外面,然后进行剩下的积分操作。例如,4 * √x 可以写成 4 * x^(1/2),然后按照积分规则进行计算。
在这个视频中给出的练习的解法是什么?
-在练习中,首先将平方根拆开,得到 √16 * √x。16 的平方根是 4,提到外面后,剩下的就是对 √x 的积分,最终得到的结果是 8/3 * √x。
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Produkt-, Quotienten- und Kettenregel
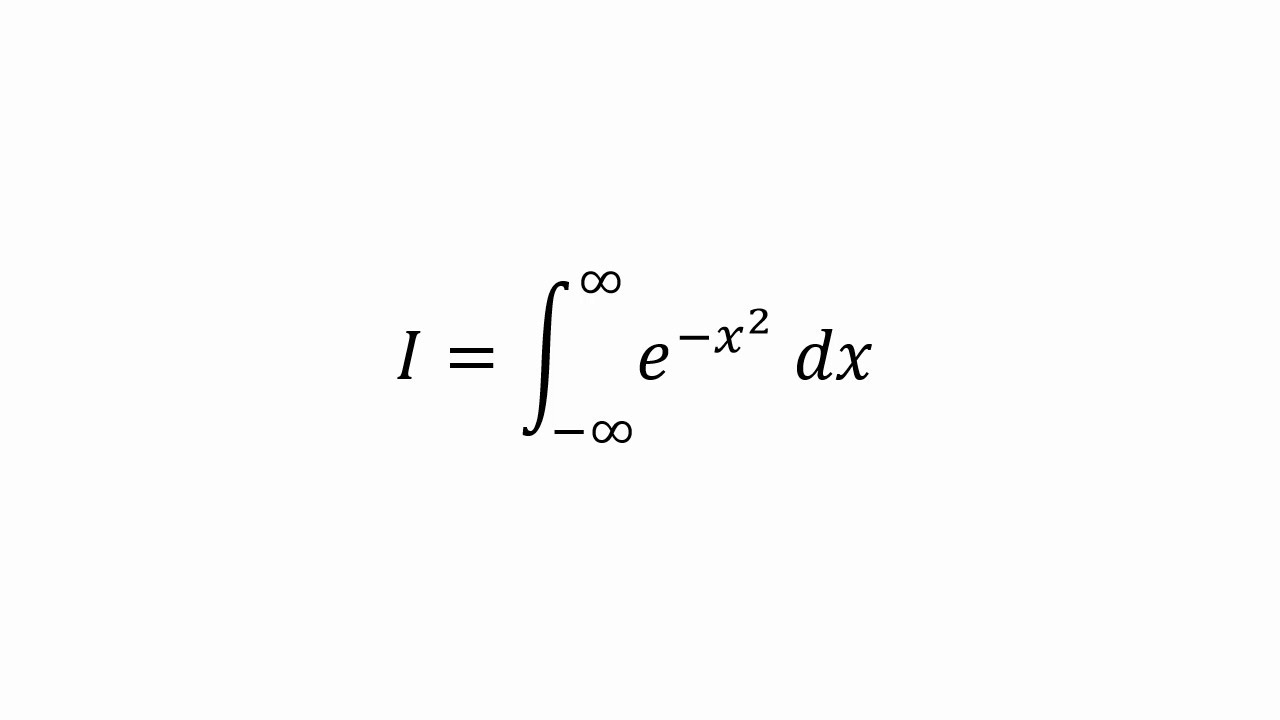
The Gaussian Integral

FISIKA KELAS X - HUKUM GRAVITASI NEWTON (PART 1) | GAYA GRAVITASI

Integración por sustitución | Ejemplo 16 | Seno cuadrado por coseno

Integración por fracciones parciales | Ejemplo 1 División
But what is the Fourier Transform? A visual introduction.

[Part 1] Making a Video Player in Godot with FFmpeg - Tutorial
5.0 / 5 (0 votes)
