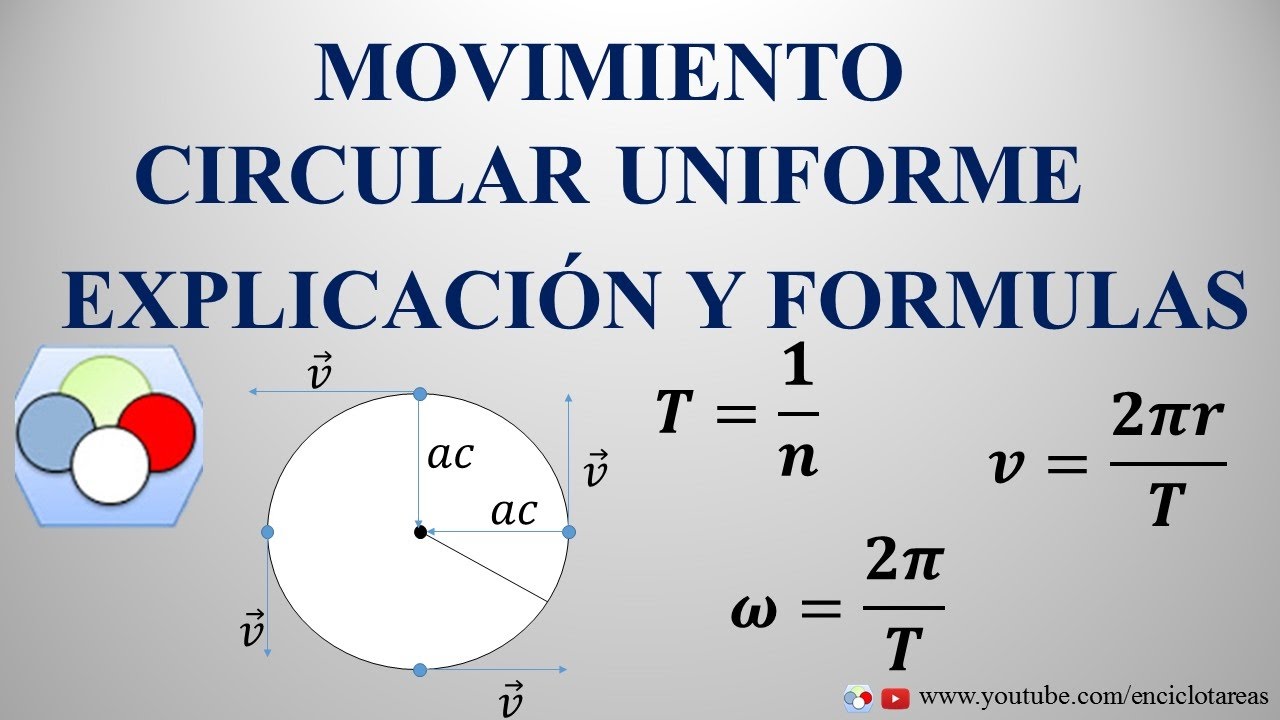
Movimiento Circular Uniforme ( M.C.U. ) | Teoría + Ejercicios
Summary
TLDREn este video se explica el concepto de movimiento circular uniforme, en el cual un cuerpo describe una trayectoria circular con rapidez constante. Se aborda la velocidad angular, cómo calcularla en diferentes situaciones, como cuando se conoce el ángulo recorrido, la frecuencia o el periodo del movimiento. Se presentan ejemplos como el movimiento de un ventilador, las manecillas de un reloj y un péndulo. A través de ejercicios prácticos, el video muestra cómo utilizar fórmulas específicas para obtener la velocidad angular en radianes por segundo, tanto en forma decimal como en función de pi.
Takeaways
- 😀 El Movimiento Circular Uniforme (MCU) implica un cuerpo que describe una trayectoria circular con rapidez constante.
- 😀 En el MCU, la rapidez angular es constante, lo que significa que el objeto recorre ángulos iguales en tiempos iguales.
- 😀 La **velocidad angular** o rapidez angular se mide en radianes por segundo (rad/s) y describe la velocidad de rotación del cuerpo.
- 😀 La velocidad angular se puede calcular de tres formas: con el ángulo recorrido y el tiempo, con la frecuencia, o con el periodo.
- 😀 La fórmula para calcular la velocidad angular cuando conocemos el ángulo recorrido y el tiempo es: ω = Ángulo / Tiempo.
- 😀 Si conocemos la frecuencia (vueltas por segundo), la velocidad angular se calcula con la fórmula: ω = 2π × Frecuencia.
- 😀 Cuando conocemos el periodo (el tiempo que tarda en dar una vuelta completa), la fórmula es: ω = 2π / Periodo.
- 😀 La frecuencia se mide en hertz (Hz), que equivale a vueltas por segundo, ciclos por segundo, o revoluciones por segundo.
- 😀 En un ventilador que gira a 15 revoluciones por segundo, la velocidad angular es de 30π radianes por segundo, o aproximadamente 94.2 rad/s.
- 😀 En un tocadiscos cuyo periodo es 0.05 segundos, la velocidad angular es 40π radianes por segundo, o aproximadamente 125.6 rad/s.
- 😀 El producto 2π radianes representa una vuelta completa, o 360 grados, lo que es esencial para calcular la velocidad angular.
Q & A
¿Qué es el movimiento circular uniforme?
-Es un tipo de movimiento en el que un cuerpo se mueve a lo largo de una trayectoria circular con rapidez constante, recorriendo ángulos iguales en tiempos iguales.
¿Cómo se representa la rapidez en el movimiento circular uniforme?
-La rapidez en el movimiento circular uniforme se representa con la letra griega 'omega' (ω), que indica la velocidad angular o rapidez angular.
¿Qué es la velocidad angular?
-La velocidad angular es la medida de la velocidad de rotación de un objeto, y se define como el ángulo recorrido por unidad de tiempo. Su unidad de medida es el radián por segundo (rad/s).
¿Cuáles son algunos ejemplos de movimiento circular uniforme?
-Algunos ejemplos incluyen la rueda de la fortuna, las llantas de un coche a velocidad constante, las manecillas de un reloj, las aspas de un ventilador o un molino de viento.
¿Cómo se calcula la velocidad angular cuando conocemos el ángulo recorrido y el tiempo?
-La velocidad angular se calcula dividiendo el ángulo recorrido en radianes por el tiempo en segundos. La fórmula es: ω = θ / t.
En el ejemplo del péndulo, ¿cómo se calculó la velocidad angular?
-En el ejemplo, el ángulo de giro del péndulo fue de 0.89 radianes y el tiempo de 3 segundos. Al aplicar la fórmula ω = θ / t, la velocidad angular resultó ser 0.29 rad/s.
¿Qué es la frecuencia y cómo influye en la velocidad angular?
-La frecuencia es el número de vueltas o ciclos por unidad de tiempo, y se mide en hertz (Hz). La velocidad angular se calcula multiplicando 2π por la frecuencia: ω = 2π × f.
En el caso del ventilador que gira a 15 revoluciones por segundo, ¿cómo se calculó la velocidad angular?
-Usando la fórmula ω = 2π × f, donde la frecuencia f es 15 revoluciones por segundo. El resultado es 30π rad/s o aproximadamente 94.2 rad/s.
¿Qué es el periodo y cómo afecta al cálculo de la velocidad angular?
-El periodo es el tiempo que tarda un cuerpo en completar una vuelta o ciclo completo. Para calcular la velocidad angular con el periodo, se utiliza la fórmula ω = 2π / T, donde T es el periodo.
En el ejemplo del tocadiscos, ¿cómo se determinó la velocidad angular?
-Dado que el periodo del tocadiscos era 0.05 segundos, se utilizó la fórmula ω = 2π / T. El resultado fue una velocidad angular de 125.6 rad/s o 40π rad/s.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)