Factorización Trinomio de la forma ax2+bx+c | Paso a paso
Summary
TLDREn este video, se introduce la factorización de trinomios de la forma x² + bx + c. Se explican las características de estos trinomios y se presenta un método para convertirlos en un formato que facilite su factorización. A través de ejemplos, se demuestra cómo aplicar este método, resaltando la importancia de identificar correctamente los términos y su orden. Además, se discute la posibilidad de trabajar con diferentes variables y exponentes, siempre siguiendo la misma lógica para lograr la factorización. El video concluye invitando a los espectadores a profundizar en el tema y practicar más.
Takeaways
- 😀 La factorización se aplica a trinomios de la forma x² + bx + c.
- 😀 Un trinomio debe tener tres términos ordenados: x², x, y término independiente.
- 😀 La mayoría de los ejercicios usan la letra x, pero se pueden aplicar a otras variables.
- 😀 Es común que el máximo exponente de la variable sea 2, pero puede ser cualquier exponente par.
- 😀 Para factorizar, primero convertimos el trinomio a la forma estándar.
- 😀 Identificar la raíz cuadrada del primer término es crucial para el proceso de factorización.
- 😀 Se busca dos números que multiplicados den c y que sumados o restados den b.
- 😀 La multiplicación de los términos en los paréntesis debe dar la expresión original al ser expandida.
- 😀 En algunos casos, se debe ajustar la expresión multiplicando y dividiendo por un número.
- 😀 Siempre se puede verificar la factorización multiplicando los factores obtenidos.
Q & A
¿Qué es un trinomio en el contexto de la factorización?
-Un trinomio es una expresión algebraica que contiene tres términos, generalmente de la forma ax² + bx + c.
¿Cómo se identifica un trinomio de la forma x² + bx + c?
-Se identifica por tener tres términos: el término cuadrático (x²), el término lineal (bx) y el término constante (c), ordenados de manera específica.
¿Qué condiciones deben cumplir los exponentes de las variables en los trinomios?
-El término cuadrático debe tener un exponente de 2 y el término lineal debe tener un exponente de 1. Si hay otras letras, su exponente debe ser un número par, y el término cuadrático debe ser la mitad de ese exponente.
¿Cuál es el método sugerido para factorizar trinomios en el video?
-El método consiste en convertir el trinomio en una forma más sencilla, donde se puede identificar la raíz cuadrada del término cuadrático y luego encontrar dos números que multiplicados den el término constante y sumados den el término lineal.
¿Qué pasos se deben seguir para factorizar el trinomio x² + 5x - 14?
-Colocamos la raíz cuadrada del término cuadrático (x) en ambos paréntesis, y luego buscamos dos números que multiplicados den -14 y sumados den 5, que son 7 y -2.
¿Cómo se puede aplicar el método de factorización a diferentes variables?
-El método es aplicable a cualquier letra, siempre que se mantenga la forma del trinomio. Por ejemplo, en lugar de x, se puede usar a, y el proceso es el mismo.
¿Qué se debe hacer si el trinomio incluye un coeficiente en el término cuadrático?
-Si el trinomio tiene un coeficiente diferente de 1 en el término cuadrático, se debe multiplicar y dividir toda la expresión por ese coeficiente para mantener la igualdad y facilitar la factorización.
¿Qué significa que la multiplicación es conmutativa en este contexto?
-Significa que el orden de los factores no altera el producto, lo que permite colocar los números multiplicados en cualquier orden dentro de la expresión.
¿Cómo se simplifica la expresión final tras factorizar?
-Al finalizar la factorización, se debe simplificar cualquier factor común en el numerador y el denominador, asegurando que se mantiene la expresión original.
¿Por qué es importante verificar el resultado de la factorización?
-Es importante verificar multiplicando los factores obtenidos para asegurarse de que se recupera la expresión original, confirmando así la correcta factorización.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Solución de límites por factorización | Ejemplo 10

LOS 10 CASOS DE FACTORIZACION En 10 minutos Cursos online
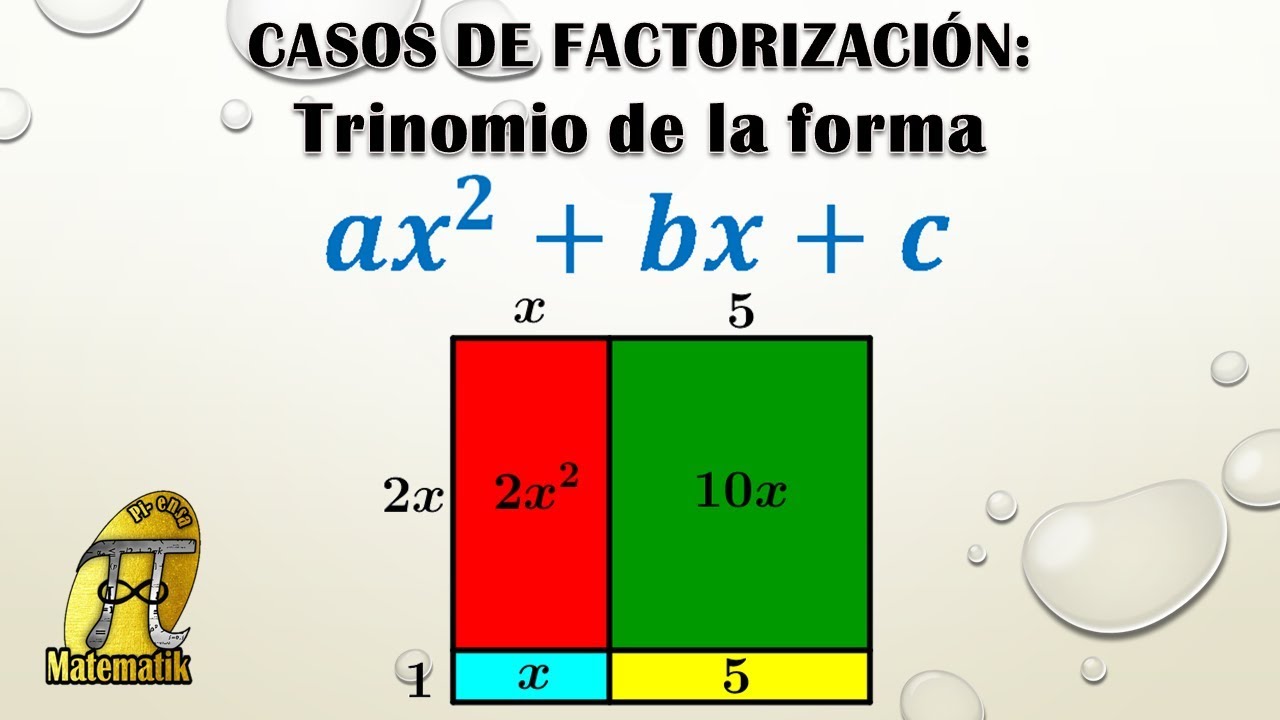
Trinomio de la forma ax^2+bx+c gráficamente | Casos de Factorización

Solución de límites por factorización | Ejemplo 3

Solución de límites por factorización | Ejemplo 4

Factorización trinomio de la forma ax2+bx+c | Ejemplo 2
5.0 / 5 (0 votes)
