Seno, coseno y tangente de 30° 45° 60° | Sin calculadora
Summary
TLDREn este video, se exploran las funciones trigonométricas de ángulos especiales: 30°, 45° y 60°. Utilizando un triángulo equilátero para 30° y 60°, se calculan el seno, coseno y tangente de ambos ángulos, demostrando sus relaciones y propiedades. Luego, se introduce un triángulo isósceles para el ángulo de 45°, derivando las funciones trigonométricas correspondientes. El instructor anima a los espectadores a practicar y a consultar otros recursos para mejorar su comprensión de las razones trigonométricas, mientras invita a suscribirse y participar en su canal.
Takeaways
- 😀 El curso se centra en las funciones trigonométricas para ángulos especiales: 30°, 45° y 60°.
- 📐 Se utiliza un triángulo equilátero para calcular las funciones trigonométricas del ángulo de 60°.
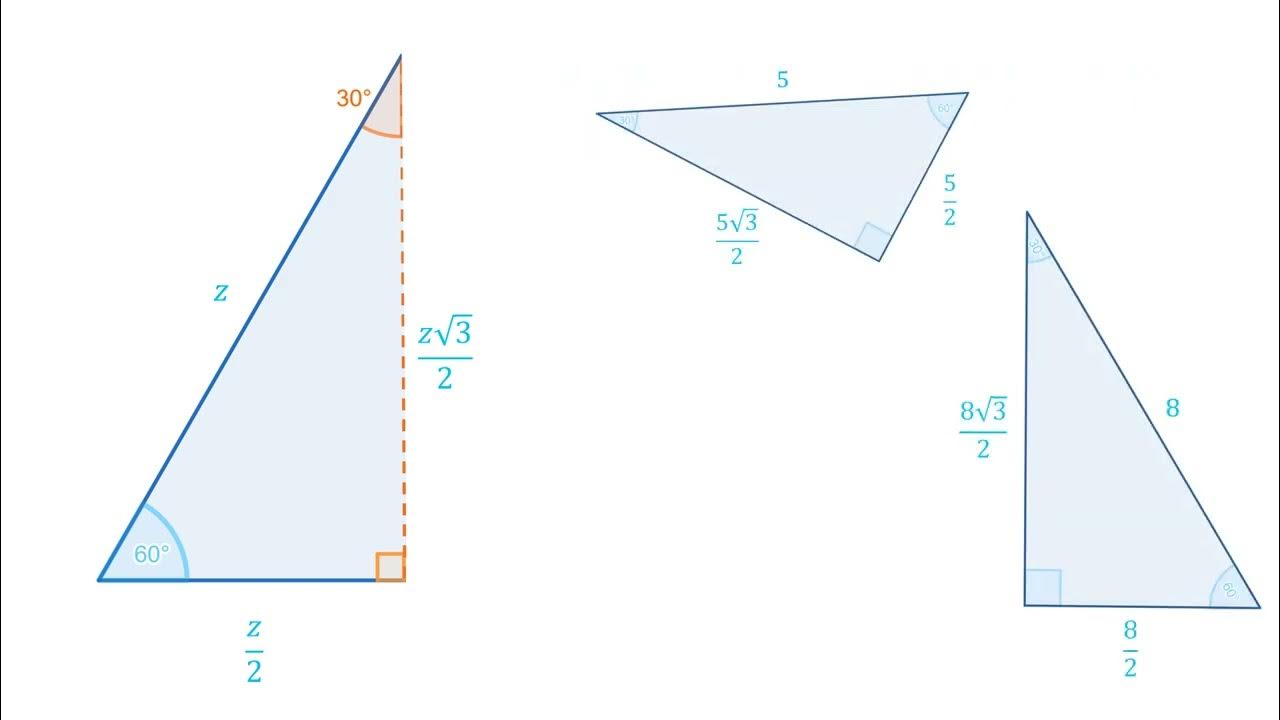
- 🔺 En un triángulo 30°-60°-90°, los lados tienen proporciones fijas: hipotenusa = 2, cateto opuesto = 1, cateto adyacente = √3.
- 📊 Para el ángulo de 30°: seno = 1/2, coseno = √3/2, tangente = 1/√3.
- 📏 El ángulo de 60° tiene las funciones trigonométricas inversas: seno = √3/2, coseno = 1/2, tangente = √3.
- ⚖️ En el triángulo isósceles de 45°, ambos catetos son iguales, facilitando los cálculos de las funciones.
- ➕ Para el ángulo de 45°: seno = 1/√2, coseno = 1/√2, tangente = 1.
- 🔄 Las funciones inversas incluyen cosecante, secante y cotangente, derivadas de las funciones originales.
- 🔍 El teorema de Pitágoras es fundamental para determinar las longitudes de los lados en los triángulos utilizados.
- 📚 Se sugiere a los estudiantes practicar y revisar el contenido anterior para reforzar su comprensión.
Q & A
¿Cuáles son las funciones trigonométricas que se encuentran para el ángulo de 30 grados?
-Las funciones trigonométricas para el ángulo de 30 grados son: seno de 30 grados es 1/2, coseno de 30 grados es raíz de 3/2, y tangente de 30 grados es 1/raíz de 3.
¿Por qué se utiliza un triángulo equilátero en el primer ejercicio?
-Se utiliza un triángulo equilátero porque todos sus lados y ángulos son iguales, lo que facilita el cálculo de las funciones trigonométricas para los ángulos de 30 y 60 grados.
¿Cómo se determina el valor de la altura de un triángulo equilátero?
-La altura de un triángulo equilátero divide el lado de abajo en dos partes iguales y se puede calcular usando el teorema de Pitágoras.
¿Qué relación existe entre los ángulos internos de un triángulo equilátero?
-Todos los ángulos internos de un triángulo equilátero miden 60 grados, y por lo tanto, la suma de los ángulos internos es 180 grados.
¿Cuáles son las funciones trigonométricas del ángulo de 60 grados?
-Las funciones trigonométricas para el ángulo de 60 grados son: seno de 60 grados es raíz de 3/2, coseno de 60 grados es 1/2, y tangente de 60 grados es raíz de 3.
¿Qué tipo de triángulo se utiliza para calcular las funciones trigonométricas del ángulo de 45 grados?
-Se utiliza un triángulo isósceles, donde dos lados son iguales y el ángulo recto forma dos ángulos de 45 grados.
¿Cómo se calcula la hipotenusa en un triángulo isósceles de 45 grados?
-Se calcula usando el teorema de Pitágoras, donde el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
¿Qué valores se obtienen para las funciones trigonométricas del ángulo de 45 grados?
-Las funciones trigonométricas para el ángulo de 45 grados son: seno de 45 grados es 1/raíz de 2, coseno de 45 grados es 1/raíz de 2, y tangente de 45 grados es 1.
¿Cuál es la importancia de las funciones trigonométricas inversas?
-Las funciones trigonométricas inversas, como la cosecante, secante y cotangente, son importantes porque permiten calcular los lados de un triángulo cuando se conocen las funciones trigonométricas básicas.
¿Qué se recomienda hacer si los conceptos no quedan claros?
-Se recomienda revisar los videos anteriores del curso para una comprensión más detallada de las funciones trigonométricas y el teorema de Pitágoras.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Círculo trigonométrico (PRIMERA PARTE)

Identidades Trigonométricas | Identidad Pitagórica | Identidades de Cofunciones |

Identidades trigonométricas de resta de ángulos | Seno y Coseno de 15° sin calculadora

Identidades trigonométricas de suma de ángulos | Seno y Coseno de 75° sin calculadora
Razones Trigonométricas en Triángulos Especiales

Cómo trazar Ángulos con Escuadra y Cartabón: 15º, 75º, 45º, 60º, 30º, 90º, 165º, 105º, 135º y más.
5.0 / 5 (0 votes)
