Vektorraum, was ist das? Im Vergleich: Menge, Gruppe, Ring, Körper | Mathe by Daniel Jung
Summary
TLDRIn diesem Video wird die strukturierte Herangehensweise an Mengen, Verknüpfungen und algebraische Strukturen erläutert. Der Fokus liegt auf den natürlichen Zahlen und deren Verknüpfungen wie Addition und Multiplikation. Der Sprecher erklärt die Konzepte von Halbgruppen, Monoiden und Gruppen sowie die Voraussetzungen für Ringe und Körper. Es wird auch darauf hingewiesen, dass Vektorräume über einem Körper definiert sind und nicht nur auf geometrische Objekte beschränkt sind. Die Darstellung von R^n als Vektorräume wird hervorgehoben, um ein besseres Verständnis für diese mathematischen Konzepte zu schaffen.
Takeaways
- 😀 Eine umfassende Betrachtung von Mengen und Verknüpfungen ist wichtig für das Verständnis von algebraischen Strukturen.
- 😀 Die natürlichen Zahlen können als Beispiel für eine Menge genutzt werden, um Verknüpfungen zu erläutern.
- 😀 Bei der Untersuchung von Verknüpfungen müssen Eigenschaften wie Abgeschlossenheit, Assoziativität, und Kommutativität beachtet werden.
- 😀 Gruppen sind spezielle Strukturen, die aus einer Menge und einer Verknüpfung bestehen, wobei nicht alle Mengen Gruppen bilden.
- 😀 Eine klare Unterscheidung zwischen Halbgruppen, Monoid, Gruppen und abelschen Gruppen ist notwendig.
- 😀 Ringe und Körper erweitern die Konzepte von Verknüpfungen, indem sie mehrere Verknüpfungen (z.B. Addition und Multiplikation) einbeziehen.
- 😀 Reelle Zahlen bilden einen Körper, was für das Verständnis von Vektorräumen entscheidend ist.
- 😀 Vektorräume sind Mengen, die über einem Körper definiert sind und können unterschiedlich viele Dimensionen haben (z.B. R², R³).
- 😀 Vektoren können nicht nur als Zahlen, sondern auch als Funktionen dargestellt werden.
- 😀 Das Verständnis der Konzepte in höheren Dimensionen (z.B. Rⁿ) ist wichtig, um algebraische Strukturen vollständig zu begreifen.
Q & A
Was sind natürliche Zahlen und wie werden sie im Kontext von Verknüpfungen verwendet?
-Natürliche Zahlen sind die Mengen, die mit 0, 1, 2 usw. beginnen. Sie werden in Verknüpfungen verwendet, um mathematische Strukturen wie Gruppen zu bilden.
Welche Eigenschaften müssen Verknüpfungen haben, um eine Gruppe zu bilden?
-Eine Gruppe muss die Eigenschaften der Abgeschlossenheit, Assoziativität, ein neutrales Element und inversen Elemente besitzen.
Was ist der Unterschied zwischen Halbgruppen, Monoiden und Gruppen?
-Halbgruppen haben nur die Assoziativität. Monoide haben zusätzlich ein neutrales Element. Gruppen haben alle drei Eigenschaften, einschließlich inverser Elemente.
Wie wird der Begriff 'Ring' in der Mathematik definiert?
-Ein Ring ist eine Menge, die zwei Verknüpfungen hat, in der Regel Addition und Multiplikation, wobei bestimmte Bedingungen gelten müssen.
Was sind die Eigenschaften eines Körpers in der Mathematik?
-Ein Körper ist eine Menge mit zwei Verknüpfungen, die die Eigenschaften von Abgeschlossenheit, Assoziativität, Identität, Inversen und Kommutativität erfüllen.
Wie unterscheiden sich Vektorräume von anderen mathematischen Strukturen?
-Ein Vektorraum ist eine Struktur, die über einem Körper definiert ist und Vektoren (die auch Funktionen sein können) als Elemente hat, im Gegensatz zu einfacheren Mengen.
Was bedeutet es, wenn gesagt wird, dass R^2 als Vektorraum betrachtet werden kann?
-R^2 ist der Vektorraum, der aus allen geordneten Paaren von reellen Zahlen besteht. Er kann nicht nur geometrisch, sondern auch algebraisch betrachtet werden.
Was sind Beispiele für andere Vektorräume neben R^2?
-Beispiele sind R^3, R^4 und allgemein R^n, wobei n jede natürliche Zahl darstellen kann.
Welche Probleme haben Lernende häufig mit dem Konzept von Körpern?
-Lernende haben oft Schwierigkeiten zu verstehen, dass reelle Zahlen einen Körper bilden und nicht nur eine Sammlung von Zahlen darstellen.
Warum ist es wichtig, die Struktur von mathematischen Konzepten zu verstehen?
-Das Verständnis der Struktur hilft dabei, die Zusammenhänge zwischen verschiedenen mathematischen Konzepten zu erkennen und diese effizient anzuwenden.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Gefahrgut: Die 1000-Punkte-Regel einfach erklärt!
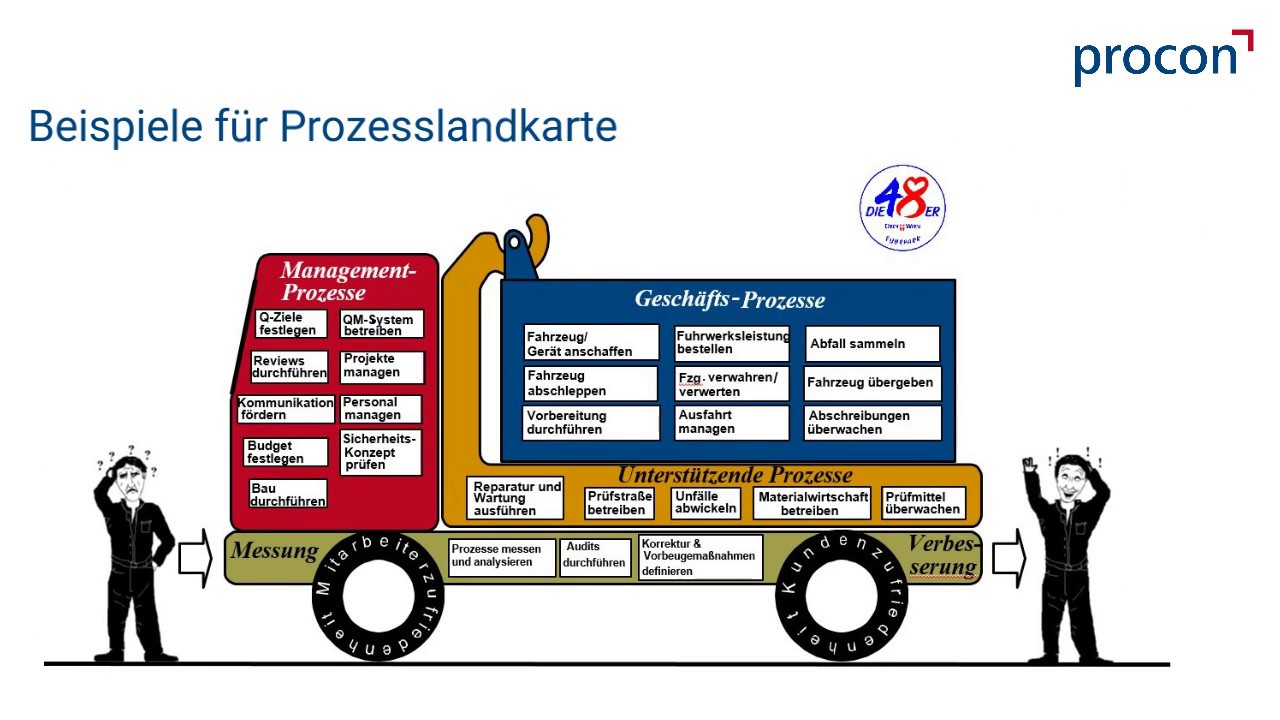
Wie erstellt man eine Prozesslandkarte?

Mathe ABITUR – Analysis, Integrale

KUDIVI 01 - Der Otto-Selle-Konflikt

Literature Review schreiben | In 3 Schritten zum aktuellen Forschungsstand 🔍

Plan B - Secret: How to narrow down countries for emigration with 5 questions! 🧳✈️”
5.0 / 5 (0 votes)