The Art of Linear Programming
Summary
TLDRThis video introduces linear programming, a powerful technique used to solve optimization problems. The presenter explains the fundamentals through a farming example, showing how to maximize profit using limited resources. The video covers both geometric and algorithmic solutions, including the Simplex method, while discussing the significance of duality in proving optimality. It also touches on the complexities of integer linear programming, illustrating its challenges with the knapsack problem. Overall, the video provides a foundational overview of linear programming, its methods, and its real-world applications.
Takeaways
- 💡 Linear Programming (LP) is a powerful mathematical technique used to solve optimization problems by maximizing or minimizing a linear objective function subject to linear constraints.
- 🌱 Example problem: A farmer has a limited amount of seeds and fertilizer. The goal is to maximize profit by planting a combination of potato and carrot crops, using LP to find the optimal solution.
- 📈 In LP, variables represent quantities (e.g., how much to plant), and the objective function is a formula (e.g., total profit) that needs to be optimized.
- 🗺️ Visualizing LP problems: The constraints create a feasible region, and the solution is found by moving along this region in the direction that maximizes the objective function.
- 🗝️ The Simplex Method is a key algorithm for solving LP problems, moving from vertex to vertex within the feasible region to find the optimal solution.
- 👨🎓 George B. Dantzig, inventor of the Simplex Method, is famous for solving two previously unsolved problems thinking they were just homework assignments.
- 🔗 Duality in LP: Every linear program has a 'dual' problem, and the duality theorem helps confirm whether the solution to the original ('primal') problem is optimal.
- 🔢 Integer Linear Programming (ILP) is a variant where variables are restricted to integers, making the problem significantly harder (often NP-hard).
- 🎒 Example ILP problem: The knapsack problem involves selecting items to maximize total value without exceeding a weight limit, showcasing the complexity of ILP.
- 🚀 Tools like the Python 'pulp' package can efficiently solve both LP and ILP problems, making complex real-world applications feasible.
Q & A
What is the main goal of the farmer's problem described in the video?
-The main goal is to maximize the profit from planting potato and carrot seeds, given limited amounts of seeds and fertilizer. The profit is calculated using a linear objective function, which is then maximized through linear programming.
How does linear programming solve the farmer’s problem?
-Linear programming solves the problem by formulating it with variables and constraints. The amount of potatoes and carrots planted is represented by variables, and the constraints involve the available seeds and fertilizer. The objective function representing profit is maximized by finding the optimal combination of planted seeds that satisfies the constraints.
What role do inequalities play in linear programming?
-Inequalities define the constraints in a linear program. They restrict the range of possible values for the variables. In the farmer’s problem, inequalities represent the limits on the amounts of potato seeds, carrot seeds, and fertilizer, ensuring that none of the resources are exceeded.
Why does the simplex method focus on moving between vertices of the feasible region?
-The simplex method focuses on vertices because the optimum solution of a linear program is always located at one of the vertices of the feasible region. By moving from one vertex to another, the method guarantees that it will find the maximum or minimum value of the objective function.
What is the significance of George B. Dantzig in linear programming?
-George B. Dantzig is credited with developing the simplex method, a fundamental algorithm in linear programming. His contribution significantly advanced the field, and the method remains one of the most widely used techniques for solving linear programs.
What are slack variables and why are they used in the simplex method?
-Slack variables are introduced to convert inequalities into equalities, which simplifies calculations in linear programming. By adding slack variables, the problem can be redefined in a way that makes it easier to apply the simplex method and keep track of which constraints are active.
What is duality in linear programming, and why is it important?
-Duality in linear programming refers to the relationship between two related optimization problems: the primal and the dual. The dual provides an upper bound on the primal problem's objective function. If both have optimal solutions, the values of the objective functions will be equal, which is known as the strong duality theorem. Duality helps in proving the optimality of a solution and can sometimes lead to more efficient algorithms.
Why is integer linear programming (ILP) harder than regular linear programming?
-Integer linear programming is harder because it restricts the solution to integer values, which significantly increases the complexity. Unlike linear programming, which can be solved in polynomial time, ILP is often NP-hard, meaning that no known polynomial-time algorithm exists for solving all cases efficiently.
What is the knapsack problem, and how is it formulated as an integer linear program?
-The knapsack problem involves selecting a set of items with given weights and prices to maximize the total price without exceeding a weight limit. It is formulated as an integer linear program by using binary variables (0 or 1) to represent whether each item is included or not. Constraints ensure that the total weight does not exceed the limit, and the objective function maximizes the total price of the selected items.
What is Dantzig's pivot rule, and how is it applied in the simplex method?
-Dantzig's pivot rule is used to select which variable to loosen in the simplex method. It selects the variable with the largest positive coefficient in the objective function, which corresponds to the steepest direction towards the optimum solution. This ensures that each pivot moves the solution closer to the optimal value.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

1 Linear Programming - Concept17072020
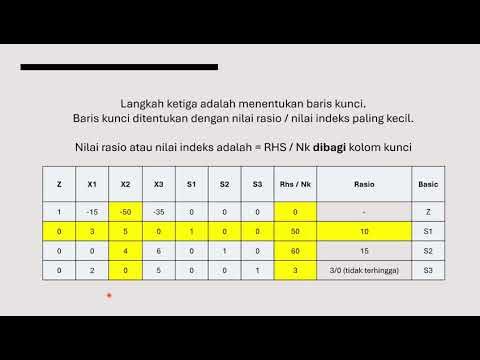
Metode Simplex dengan 3 Variable - Riset Operasional

ART TEACHES MATHEMATICS IN THE MODERN WORLD-LESSON 1: INTRO TO LINEAR PROGRAMMING

Pemrograman Dinamis - Berpikir Komputasional | Informatika XI

MK Kuantitatif - Linier Programming Metode Simpleks
PROGRAM LINIER - METODE GRAFIK - RISET OPERASI
5.0 / 5 (0 votes)
