Longitudinal standingg waves
Summary
TLDRThe video explores the concept of standing waves in pipes, focusing on both closed and open pipes. It demonstrates how waves superimpose and create standing waves when boundary conditions are met. The instructor explains harmonic modes, displacement nodes, pressure nodes, and the fundamental tone in both closed-closed and open-open pipe systems. The discussion also extends to closed-open configurations, emphasizing the odd harmonic pattern. Key equations for calculating wave speed, wavelength, and frequency are introduced, linking them to real-world examples like air and water. The video concludes with caution about the terminology used in problems and books.
Takeaways
- 📌 Standing waves can form in a pipe filled with gas, where waves reflect and superimpose if boundary conditions are met.
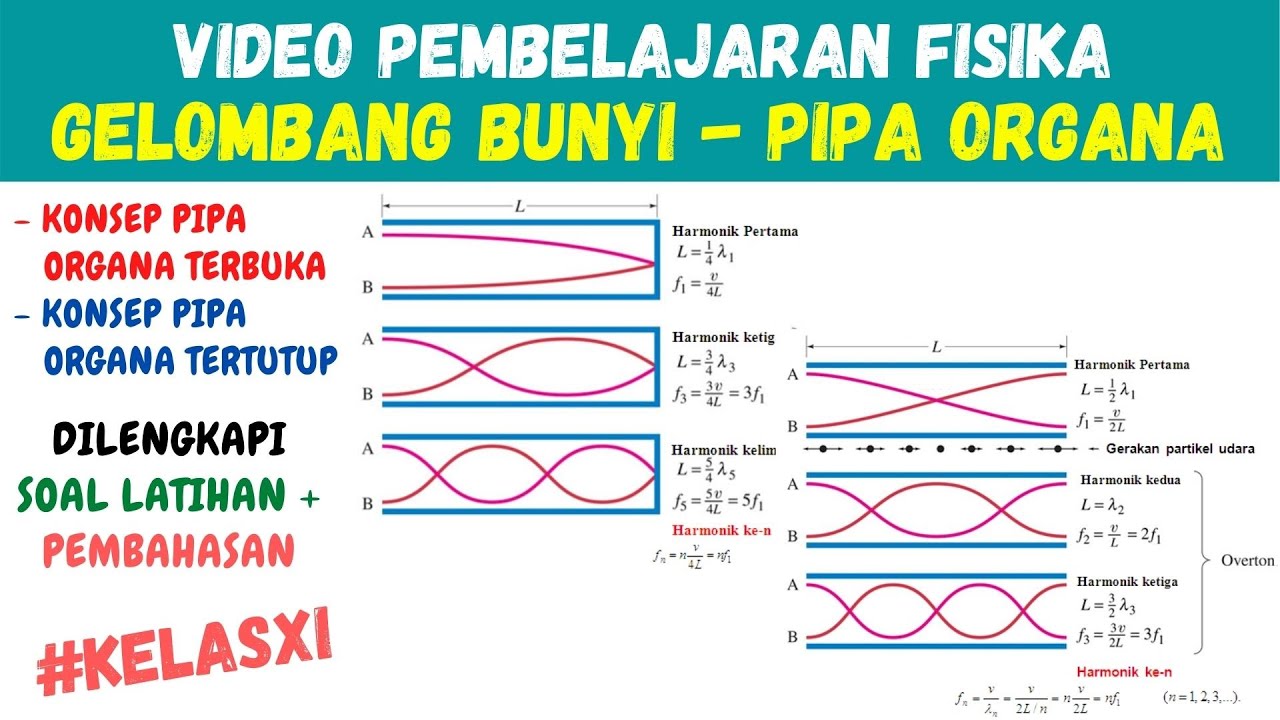
- 🎵 In a closed-closed pipe, standing waves require nodes at both ends, and the first mode of oscillation corresponds to the fundamental tone.
- 🔄 The next harmonic in a closed-closed pipe will have an additional node, allowing more half-wavelengths within the pipe.
- 📏 The wavelength and frequency of the standing waves can be calculated using the equation L = n * λ/2, where n is the number of half-wavelengths.
- 📦 The speed of sound in a medium like air or water depends on the bulk modulus and density of the medium.
- 🔊 In an open-open pipe, standing waves can form with pressure nodes at both ends, even without a physical barrier.
- 🌡️ Atmospheric pressure serves as a reference point for pressure waves in open pipes, affecting how waves reflect and form nodes.
- ⚖️ Pressure nodes and displacement nodes are related but offset by 90°, creating alternating regions of high pressure and no movement.
- 🔔 For open-closed pipes, only odd-numbered harmonics are possible, as they involve quarter-wavelengths fitting into the length of the pipe.
- 📚 The terms harmonic, overtone, and fundamental can be confusing, so be mindful of the specific definitions used in problems and discussions.
Q & A
What is the main focus of the discussion in the script?
-The main focus of the discussion is on standing waves in pipes, specifically longitudinal waves in closed and open pipes, and how standing waves are formed under different boundary conditions.
What are standing waves, and how are they formed in a pipe?
-Standing waves are formed when two waves of the same frequency and amplitude travel in opposite directions and interfere with each other. In a pipe, they are created when a wave is sent through the pipe, gets reflected at the boundary, and overlaps with the incoming wave.
What is the significance of nodes and antinodes in standing waves?
-Nodes are points where there is no displacement, and antinodes are points where the displacement is maximum. In standing waves within a pipe, nodes and antinodes represent areas where the medium's molecules either remain still (nodes) or oscillate with maximum amplitude (antinodes). These positions depend on the pipe's boundary conditions.
How does the first harmonic or fundamental mode of oscillation look in a closed-closed pipe?
-In a closed-closed pipe, the first harmonic (or fundamental mode) has nodes at both ends of the pipe, with a single antinode in the middle. The length of the pipe fits half a wavelength of the standing wave.
How does the number of harmonics affect the wave pattern in a pipe?
-As the number of harmonics increases, more nodes and antinodes form within the pipe. The second harmonic, for instance, has two nodes inside the pipe and two half-wavelengths fit within the length of the pipe. The third harmonic has three nodes and so on.
What is the difference between transverse waves and longitudinal waves as discussed in the script?
-Transverse waves involve oscillations perpendicular to the direction of wave travel, while longitudinal waves involve oscillations parallel to the wave's direction. In the script, the focus is on longitudinal waves within pipes.
What equation is used to determine the wavelength and frequency of standing waves in a pipe?
-The equation used is λ = V / f, where λ is the wavelength, V is the speed of sound in the medium, and f is the frequency. The relationship between the pipe's length and the number of wavelengths that fit inside the pipe is also essential for determining the harmonic modes.
How do open-open and closed-closed pipes differ in terms of boundary conditions for standing waves?
-In closed-closed pipes, both ends are closed, so nodes must exist at both ends. In open-open pipes, both ends are open, so antinodes form at both ends, allowing standing waves to form despite the absence of physical barriers.
What happens when you have a closed-open pipe, and how does this affect the standing wave pattern?
-In a closed-open pipe, there is a node at the closed end and an antinode at the open end. The standing wave pattern is different because only odd harmonics (1st, 3rd, 5th) are possible, with each fitting quarter wavelengths of the wave inside the pipe's length.
Why can only odd harmonics occur in a closed-open pipe?
-Only odd harmonics occur in a closed-open pipe because the wave must have a node at the closed end and an antinode at the open end. This arrangement only allows quarter wavelengths to fit in the pipe, and thus the harmonics must fit an odd number of quarter wavelengths.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
Fisika Kelas 11 - PIPA ORGANA Terbuka dan Tertutup

Gelombang Bunyi • Part 3: Sumber Bunyi (Dawai, Pipa Organa Terbuka dan Tertutup)

The Physics of Music: Crash Course Physics #19

GELOMBANG BUNYI PART 5 (materi pot)

Sebuah seruling yang memiliki kolom udara terbuka pada kedua ujungnya memiliki nada atas kedua de...

Effects of Fluid Compressibility
5.0 / 5 (0 votes)
