GELOMBANG BUNYI PART 5 (materi pot)

Summary

In this lesson, the instructor discusses the concept of sound sources, focusing on closed organ pipes and their resonance properties. Using relatable examples like blowing over a bottle, the instructor explains the frequency of the fundamental note and harmonics in closed pipes. The explanation covers the relationship between the number of antinodes and nodes, and how the frequencies of higher harmonics follow an odd-numbered pattern (1, 3, 5, etc.). The video concludes with a demonstration of how resonance occurs when the frequencies of two pipes match, and it encourages further learning through practice and sharing knowledge with peers.

Takeaways

• 😀 The main topic discussed is the concept of sound sources, focusing on closed-end organ pipes.
• 😀 A closed-end organ pipe is illustrated by a bottle that, when blown, produces sound.
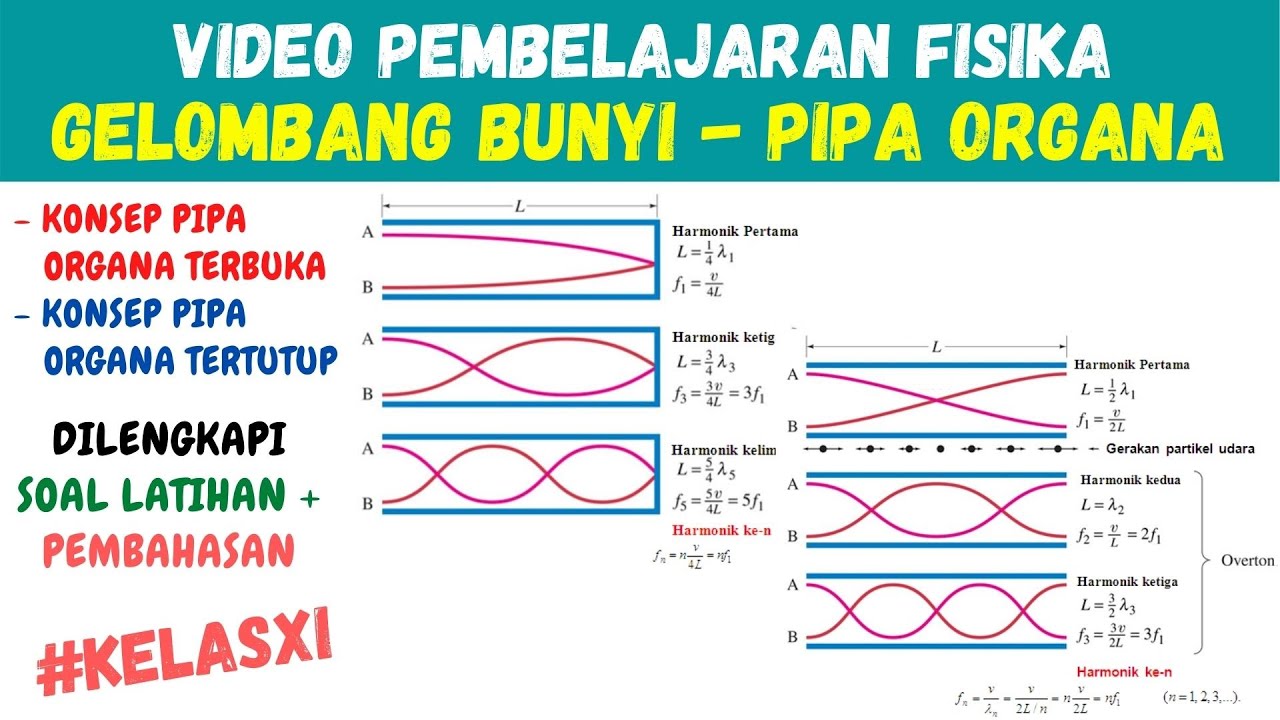
• 😀 The frequency of the fundamental note (F0) for a closed-end organ pipe is given by the formula F0 = pi / 4L, where L is the length of the pipe.
• 😀 The frequencies for overtones in a closed-end organ pipe follow a pattern of odd multiples of the fundamental frequency (1, 3, 5, 7, etc.).
• 😀 In the case of closed-end organ pipes, the number of nodes (simultaneous) corresponds with the number of antinodes (perceived 'loops') in the sound wave.
• 😀 The relationship between the number of nodes and antinodes indicates the harmonic series in a closed-end organ pipe.
• 😀 For a given length L, the fundamental frequency is calculated as pi / 4L, and higher frequencies (F1, F2, F3, etc.) are based on odd-numbered multiples.
• 😀 The calculation for F1 (first overtone) is 3 times the fundamental frequency, F2 is 5 times the fundamental frequency, and so on.
• 😀 Resonance is discussed as the phenomenon where two systems vibrate at the same frequency, resulting in amplification of the sound, which can occur between open and closed-end pipes.
• 😀 The script also includes guidance on solving problems related to the resonance between open and closed-end pipes, particularly in terms of matching their frequencies and calculating pipe lengths.

Q & A

What is the key difference between an open organ pipe and a closed organ pipe?

The key difference is that in an open organ pipe, both ends are open, while in a closed organ pipe, one end is closed and the other is open. This results in different wave patterns and frequencies.

What is an example of a closed organ pipe?

An example of a closed organ pipe is a bottle. When you blow across the opening, it produces sound, which is a simple representation of a closed organ pipe.

How is the frequency of the fundamental note (F0) in a closed organ pipe calculated?

The frequency of the fundamental note (F0) for a closed organ pipe is given by the formula f0 = v / 4L, where v is the speed of sound and L is the length of the pipe.

How are the harmonic frequencies of a closed organ pipe related?

The harmonic frequencies of a closed organ pipe follow a pattern of odd integers. The first harmonic (F0) is the fundamental frequency, the second harmonic (F1) is 3 times F0, the third harmonic (F2) is 5 times F0, and so on.

Why is the frequency ratio for harmonics in a closed organ pipe only based on odd numbers?

This happens because in a closed organ pipe, only odd harmonics are present due to the boundary conditions at the closed end (a node) and the open end (an antinode), limiting the possible standing wave patterns.

How does the number of nodes and antinodes relate to the frequencies of a closed organ pipe?

The number of nodes and antinodes in a closed organ pipe corresponds to the harmonic number. For example, in the first harmonic (F0), there is one node at the closed end, and the pipe's length is one-quarter of the wavelength.

How does the concept of resonance apply to organ pipes?

Resonance occurs when two objects or systems vibrate at the same frequency. In the case of organ pipes, resonance happens when the frequencies of the pipes match, leading to a strong and sustained sound. For instance, a pipe organ can produce resonance between open and closed pipes.

What is the formula for the frequency of the first harmonic in an open organ pipe?

The formula for the first harmonic (F0) in an open organ pipe is f0 = v / 2L, where v is the speed of sound and L is the length of the pipe.

Can the frequency of a pipe organ be changed by altering its length?

Yes, the frequency of a pipe organ can be changed by altering the length of the pipe. A longer pipe results in a lower frequency, while a shorter pipe produces a higher frequency.

What is an example of a resonating situation involving an organ pipe?

An example of a resonating situation is when an open organ pipe and a closed organ pipe resonate at the same frequency. This occurs when the frequency of the first harmonic of the open pipe matches the frequency of a higher harmonic in the closed pipe, resulting in resonance.