Operaciones con funciones (Suma, resta, multiplicación y división) (Ejemplo 2)
Summary
TLDREn este vídeo tutorial de 'Mate, fácil', se explican las operaciones básicas de suma, resta, multiplicación y división de funciones. Se utilizan dos funciones específicas para ilustrar cómo realizar estas operaciones algebraicas paso a paso. Se enfatiza la importancia de la simplificación de términos semejantes y la diferencia de orden en operaciones como la resta y la división. Al final, se anima a los espectadores a practicar estos conceptos y a suscribirse para recibir más contenido educativo.
Takeaways
- 🔢 En el vídeo, se explica cómo realizar operaciones básicas con funciones: suma, resta, multiplicación y división.
- 📐 Se comienza con la suma de funciones, donde f(x) + g(x) = (x^2 - 3) + (3 - x) simplifica a x^2 - x.
- ➖ Al realizar la resta f(x) - g(x), se obtiene x^2 + x - 6, y se destaca que el orden importa en la resta.
- 🔄 Se muestra que la resta g(x) - f(x) da un resultado diferente, destacando la importancia del orden en las operaciones.
- 💡 Se explica que para la multiplicación de funciones, se multiplican los términos de cada función entre sí, resultando en x^3 - x^3 - 9 + 3x.
- 📉 La división de funciones se presenta como la división de f(x) entre g(x), que se escribe con una línea horizontal y se simplifica a (x^2 - 3)/(3x - x).
- 🔄 Se enfatiza que, al igual que en la resta, el orden es importante en la división de funciones.
- 📚 Se invita a los espectadores a practicar estas operaciones con fracciones, sugiriendo que el procedimiento es similar.
- 👍 Se anima a los espectadores a dar like, comentar y suscribirse para recibir más contenido similar.
- 📢 Se menciona que en futuros videos se mostrará el procedimiento para realizar estas operaciones con fracciones.
Q & A
¿Qué funciones se utilizan en el vídeo para ejemplificar las operaciones aritméticas?
-Se utilizan dos funciones: f(x) = x^2 - 3 y g(x) = 3 - x.
¿Cómo se calcula la suma de las funciones f(x) y g(x)?
-La suma se calcula como (f + g)(x) = f(x) + g(x) = (x^2 - 3) + (3 - x). Al simplificar, se obtiene x^2 - x.
Cuál es el resultado de la resta f(x) - g(x)?
-El resultado es (f - g)(x) = f(x) - g(x) = (x^2 - 3) - (3 - x). Al simplificar, se obtiene x^2 + x - 6.
¿Cuál es la diferencia entre la suma y la resta de funciones en términos de orden?
-En la suma, el orden no importa, pero en la resta, el orden importa. Esto se ve reflejado en los resultados (f - g)(x) y (g - f)(x), que son diferentes.
¿Cómo se calcula la multiplicación de las funciones f(x) y g(x)?
-La multiplicación se calcula como (f * g)(x) = f(x) * g(x). Al multiplicar (x^2 - 3) por (3 - x), se obtiene x^3 - x^2 - 3x + 9.
¿Qué significa la división de funciones y cómo se calcula?
-La división de funciones es dividir una función entre otra, y se calcula como (f / g)(x) = f(x) / g(x). En el vídeo, se muestra que (f / g)(x) = (x^2 - 3) / (3 - x).
¿Por qué es importante el orden en la división de funciones?
-El orden es importante en la división de funciones porque puede cambiar el resultado. Esto se demuestra al calcular (g / f)(x), que es diferente a (f / g)(x).
¿Cómo se simplifica la división (f / g)(x) = (x^2 - 3) / (3 - x)?
-La división (f / g)(x) = (x^2 - 3) / (3 - x) no se puede simplificar más allá de lo que se muestra en el vídeo, ya que no hay factores comunes que puedan ser cancelados.
¿Qué se debe tener en cuenta al realizar operaciones con fracciones en el contexto de funciones?
-Al realizar operaciones con fracciones en funciones, se deben seguir los procedimientos estándar de suma, multiplicación y división de fracciones, asegurándose de que los términos se simplifiquen lo más posible.
¿Cómo se sugiere practicar estas operaciones con funciones?
-Se sugiere practicar estas operaciones realizando el ejercicio propuesto en el vídeo y repasando el tema de fracciones para tener una comprensión más sólida antes de intentar operaciones más complejas.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
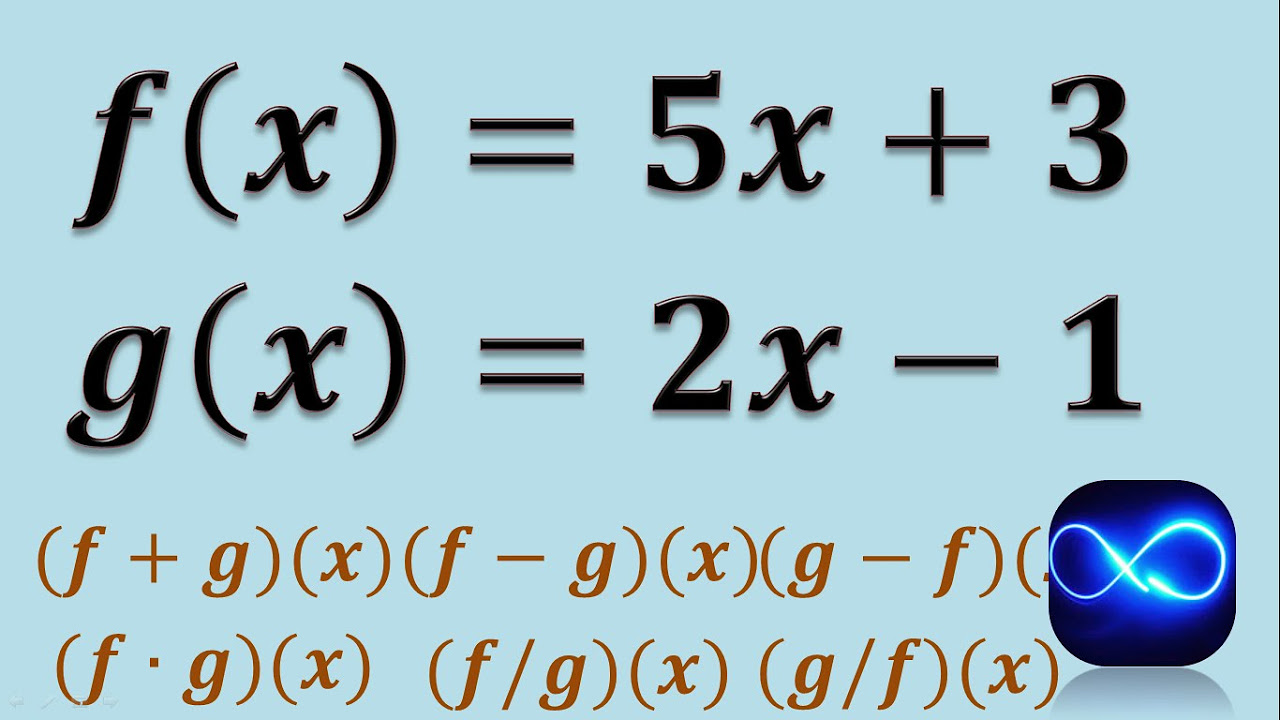
Operaciones con funciones (Suma, resta, multiplicación y división) (Ejemplo 1)

Operaciones con funciones video 1 | Cálculo diferencial - Vitual

Pensamiento matemático 3. Progresión 3a. Suma de funciones
Multiplicar, dividir, sumar y restar en Excel

Jerarquía de las operaciones | Introducción
Introducción a Excel
5.0 / 5 (0 votes)
