5 Lineare Funktionen Werkzeuge - Aufstellen einer Funktionsgleichung aus zwei Punkten
Summary
TLDRDas Video skizziert die Methode, eine lineare Funktionsgleichung aus zwei gegebenen Punkten zu bestimmen. Es zeigt, wie man zeichnerisch und rechnerisch vorgeht, um die Gleichung zu finden. Es erklärt, wie man die Steigung und den y-Achsenabschnitt ablesen kann, um die allgemeine Funktionsgleichung zu erhalten. Anschließend wird gezeigt, wie man durch Einsetzen der Punkte in die Gleichung und Anwendung eines linearen Gleichungssystems die Steigung (m) und den y-Achsenabschnitt (b) berechnet. Das Video bietet auch ein praktisches Beispiel, um die Theorie zu veranschaulichen.
Takeaways
- 📐 Die Aufgabe ist es, eine Funktionsgleichung aus zwei gegebenen Punkten zu bestimmen.
- 🖊 Die Lösung beginnt mit der graphischen Darstellung der Geraden, die durch die Punkte geht.
- 📉 Der y-Achsenabschnitt und die Steigung der Geraden werden aus der graphischen Darstellung ablesbar.
- 🔢 Die allgemeine Funktionsgleichung einer Geraden ist y = mx + b, wobei m die Steigung und b der y-Achsenabschnitt ist.
- 📝 Die Punkte werden in die allgemeine Funktionsgleichung eingesetzt, um ein lineares Gleichungssystem zu erhalten.
- ➖ Das lineare Gleichungssystem wird durch Subtraktion gelöst, um die Steigung m zu finden.
- 🔄 Die gefundene Steigung wird dann in eine der ursprünglichen Gleichungen eingesetzt, um den y-Achsenabschnitt b zu bestimmen.
- 📚 Die Funktionsgleichung wird dann aus m und b abgeleitet und mit der graphischen Darstellung verglichen.
- 🔄 Es wird gezeigt, wie man die gleiche Prozedur anwendet, um die Funktionsgleichung für verschiedene Beispiele zu finden.
- 📈 Die Verfahren werden auch auf eine Wertetabelle angewendet, um fehlende Werte in einer linearen Funktion zu ergänzen.
Q & A
Wie wird die Funktionsgleichung einer Geraden aus zwei Punkten aufgestellt?
-Man verwendet die allgemeine Funktionsgleichung einer Geraden y = mx + b, wo m die Steigung und b der y-Achsenabschnitt ist. Man setzt die Koordinaten der beiden Punkte in diese Gleichung ein, um ein lineares Gleichungssystem zu erhalten, das dann gelöst wird, um m und b zu finden.
Was ist der y-Achsenabschnitt der Geraden, die durch den Punkt P gezeichnet wird?
-Der y-Achsenabschnitt der Geraden ist -5.
Wie lautet die Steigung der Geraden, die durch den Punkt P gezeichnet wird?
-Die Steigung der Geraden ist 1/3, da sie 1 runter und 3 rechts geht.
Wie wird die Steigung einer Geraden aus einem Dreiecks gelesen?
-Die Steigung wird durch die Veränderung der y-Koordinate (Senkrechte) geteilt durch die Veränderung der x-Koordinate (Waagerechte) gelesen.
Was ist der Zweck des linearen Gleichungssystems in diesem Kontext?
-Das lineare Gleichungssystem wird verwendet, um die unbekannten Variablen m (Steigung) und b (y-Achsenabschnitt) der Funktionsgleichung einer Geraden zu bestimmen.
Wie wird die Steigung der Geraden aus dem zweiten Beispiel berechnet?
-Die Steigung der Geraden aus dem zweiten Beispiel ist 1/2, da sie 1 runter und 2 rechts geht.
Was ist der y-Achsenabschnitt der Geraden aus dem zweiten Beispiel?
-Der y-Achsenabschnitt der Geraden aus dem zweiten Beispiel ist -1.
Wie wird die Funktionsgleichung aus dem dritten Beispiel berechnet?
-Die Funktionsgleichung aus dem dritten Beispiel wird durch die Berechnung der Steigung und des y-Achsenabschnitts aus den gegebenen Punkten und deren Einsetzen in die allgemeine Funktionsgleichung y = mx + b berechnet.
Was bedeuten die Buchstaben m und b in der Funktionsgleichung y = mx + b?
-In der Funktionsgleichung y = mx + b ist m die Steigung der Geraden und b der y-Achsenabschnitt.
Wie wird der y-Achsenabschnitt aus der Wertetabelle einer linearen Funktion ermittelt?
-Der y-Achsenabschnitt aus der Wertetabelle einer linearen Funktion wird durch den Wert der y-Koordinate gefunden, wenn x gleich 0 ist.
Was ist der Zweck des Subtraktionsverfahrens in der Berechnung der Funktionsgleichung?
-Das Subtraktionsverfahren wird verwendet, um ein lineares Gleichungssystem zu lösen, indem man eine der Gleichungen von der anderen subtrahiert, um die Steigung m zu finden.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

2 Lineare Funktionen Werkzeuge - Punktprobe durchführen/Punktkoordinaten bestimmen

Vektorprodukt, Kreuzprodukt, vektorielles, äußeres Produkt, Formel | Mathe by Daniel Jung

How to genuinely unf*ck your brain (in 52 seconds)

"Wie ich die Dinge geregelt kriege" von David Allen
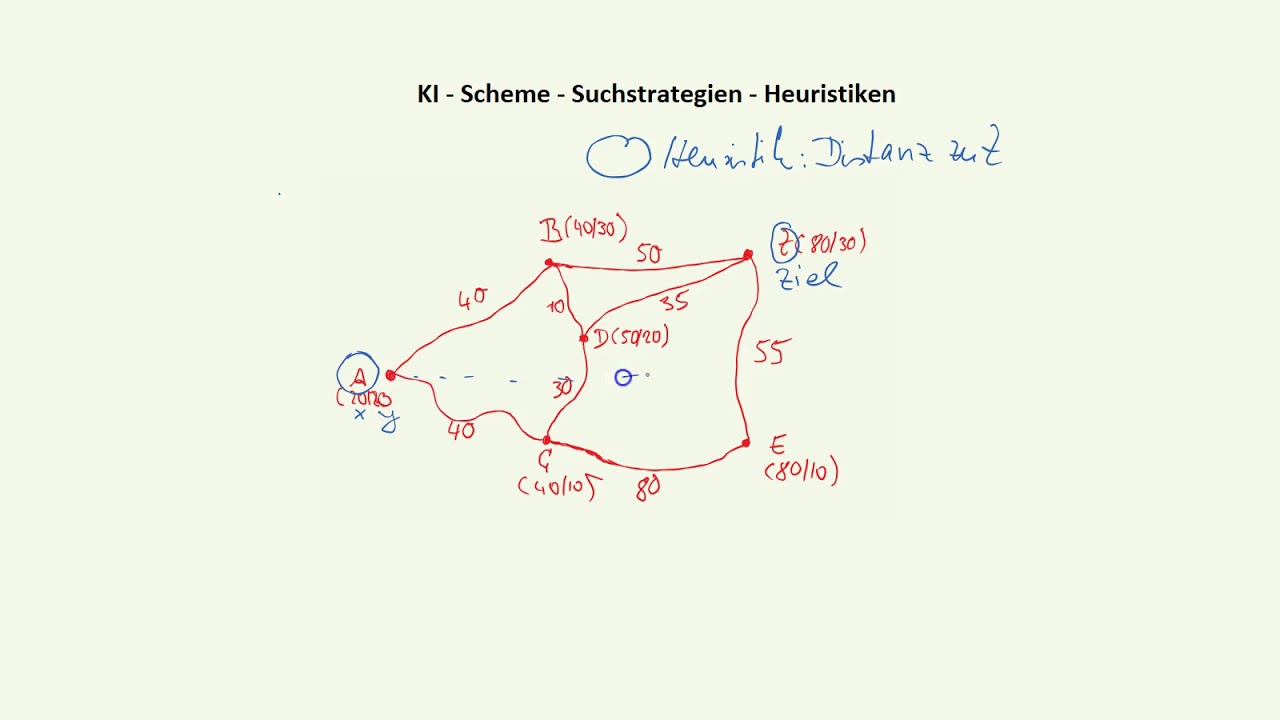
Ki und Scheme - Suchstrategien - Heuristiken

22 Ganzrationale Funktionen Differenzen und Differentialquotient an einem Punkt
5.0 / 5 (0 votes)