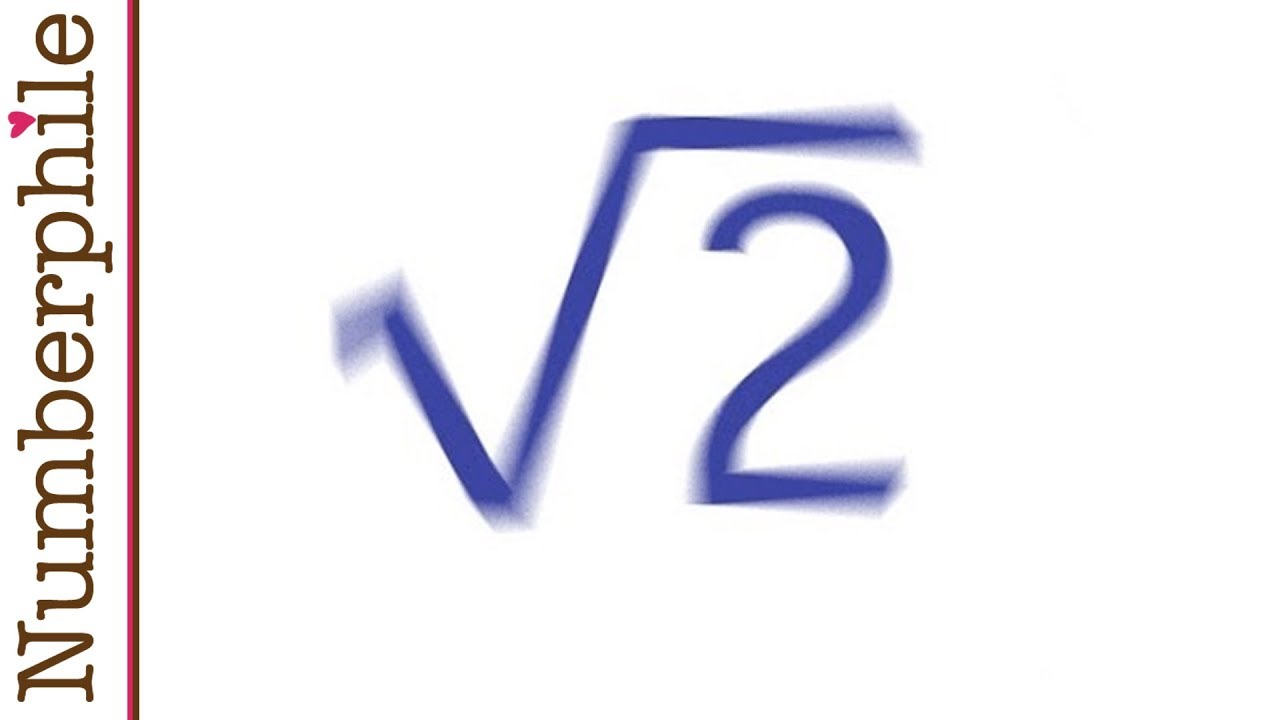DEMONSTRATION : √2 est irrationnel - Seconde
Summary
TLDRThis video script explores the irrationality of the square root of 2. It begins by defining rational numbers, exemplified by one-third, which can be expressed as a repeating decimal. In contrast, irrational numbers, like pi, have non-repeating, non-terminating decimal expansions. The script then introduces a proof by contradiction to demonstrate that the square root of 2 cannot be expressed as a fraction of two integers, leading to the conclusion that it is indeed an irrational number.
Takeaways
- 📘 The video discusses the irrationality of the square root of 2.
- 🔢 A rational number is defined as one that can be expressed as a fraction of two integers, such as one-third (1/3).
- 📏 Irrational numbers, in contrast, cannot be expressed as a simple fraction; their decimal representation is non-repeating and infinite, like the number pi (π).
- 🤔 The video aims to prove that the square root of 2 is irrational by assuming the opposite and seeking a contradiction.
- 📉 The proof uses a method of contradiction, assuming that the square root of 2 is rational and then deriving an absurdity from this assumption.
- 🔄 The assumption leads to the expression of the square root of 2 as a fraction a/b, where a and b are integers with no common divisors.
- 🔢 When squared, the equation a^2 = 2b^2 is derived, and by manipulating this equation, it's shown that both a and b must be even numbers.
- 🔄 This leads to a contradiction because it implies that a and b have a common divisor (2), which contradicts the initial assumption that they are coprime.
- 📚 The video emphasizes the importance of understanding the properties of numbers, such as the fact that the square of an odd number is always odd.
- 🏁 The conclusion is that the square root of 2 is irrational, as the initial assumption that it could be expressed as a fraction leads to a contradiction.
Q & A
What is the definition of an irrational number as explained in the video?
-An irrational number is a number that cannot be expressed as a simple fraction, meaning it cannot be written in the form of a ratio of two integers. When written in decimal form, it has a non-repeating, non-terminating pattern.
Can you provide an example of a rational number given in the video?
-Yes, one-third (1/3) is given as an example of a rational number because when divided, it results in a repeating decimal pattern of '0.3333...' indefinitely.
What is the approximate value of the irrational number pi mentioned in the video?
-The approximate value of pi given in the video is 3.14, but it is emphasized that the actual value of pi continues indefinitely without a pattern.
What method is used in the video to prove that the square root of 2 is irrational?
-The video uses a proof by contradiction, assuming that the square root of 2 is rational and then showing that this assumption leads to a contradiction, thus proving that the square root of 2 is irrational.
What does it mean for two numbers to be 'co-prime' as discussed in the video?
-Two numbers are 'co-prime' or 'relatively prime' if they have no common divisors other than 1, meaning they cannot be simplified further.
Why does the video suggest that a and b in the expression of the square root of 2 as a rational number must be co-prime?
-The video suggests that a and b must be co-prime because any fraction can be simplified to its simplest form, which is when the numerator and denominator are co-prime.
What property of squares is used in the video to deduce that a must be even if a^2 = 2b^2?
-The video uses the property that an even number is a multiple of 2. Since a^2 equals 2 times an integer (2b^2), it implies that a^2 is even, and therefore a must also be even.
How does the video demonstrate that both a and b cannot be even, leading to a contradiction?
-The video shows that if a and b are both even, then they would have a common divisor (2), which contradicts the initial assumption that a and b are co-prime.
What is the conclusion of the proof in the video regarding the rationality of the square root of 2?
-The conclusion is that the square root of 2 is not rational, as the assumption that it is rational leads to a contradiction, proving it must be irrational.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführen5.0 / 5 (0 votes)