One Sided Limits (Tagalog/Filipino Math)
Summary
TLDRIn this educational video, the host explores the concept of one-sided limits in calculus. They explain how to find the limit of a function as it approaches a certain value from the left or right, using examples like the piecewise-defined signal function and a function involving square roots. The discussion also covers when two-sided limits do not exist due to discontinuities, emphasizing the importance of understanding these mathematical concepts for a solid grasp of calculus.
Takeaways
- 📘 The video introduces the concept of limits in calculus, focusing on one-sided limits and how they are calculated.
- 🔍 The presenter explains how to find the limit of a function as it approaches a certain value, using the example of \((x-4)^2\) as \(x\) approaches 4.
- 📌 The difference between one-sided limits (left and right) and two-sided limits is discussed, with examples to illustrate the calculations.
- 📐 The video demonstrates the use of open intervals to determine the values of \(x\) that can be used to approximate the limit.
- 🚫 The importance of understanding that limits are not evaluated by substituting the value of \(x\) directly into the function is highlighted.
- 📉 The concept of discontinuity in functions is touched upon, showing how limits can be undefined at certain points.
- 🔢 Practical examples are given to show how to calculate the right-hand and left-hand limits for piecewise functions.
- 📚 The video provides a clear explanation of how to determine if a two-sided limit exists by comparing the left and right limits.
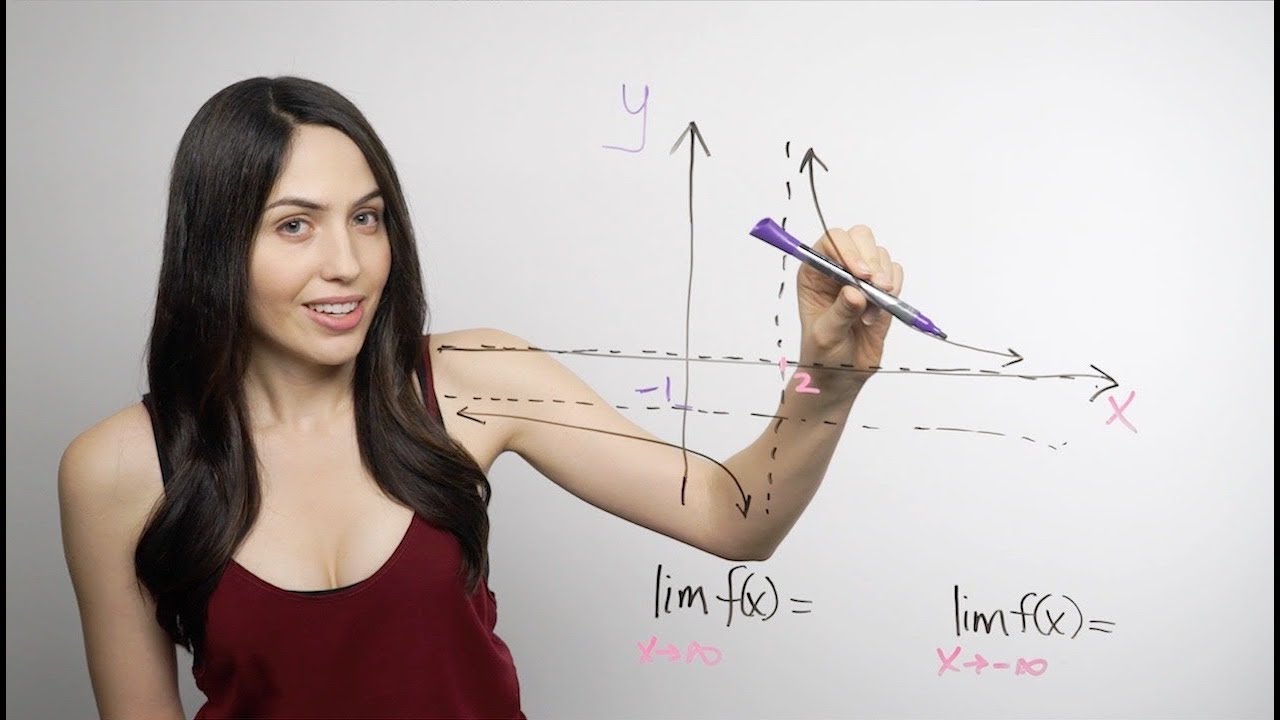
- 📊 The graphical representation of functions and their limits is briefly discussed, helping to visualize the concept.
- 💡 The presenter concludes with a summary of the key points about one-sided limits and their significance in calculus.
Q & A
What is the main topic of the video?
-The main topic of the video is an introduction to one-sided limits in calculus.
What is the function used as an example to explain one-sided limits?
-The function \((x-4)^2\) is used as an example to explain one-sided limits.
What is the significance of the number 4 in the example function?
-The number 4 is the point at which the limit of the function \((x-4)^2\) is being evaluated.
What does the term 'one-sided limit' refer to in the context of the video?
-A 'one-sided limit' refers to the limit of a function as the input approaches a certain value from either the left (negative side) or the right (positive side).
How does the video explain the difference between left-hand and right-hand limits?
-The video explains that the left-hand limit is the limit as the input approaches the value from the left (smaller values), while the right-hand limit is as the input approaches from the right (larger values).
What is the result of the one-sided limit of the function \((x-4)^2\) as \(x\) approaches 4 from the right?
-The one-sided limit of the function \((x-4)^2\) as \(x\) approaches 4 from the right is 0, denoted as \(\lim_{x \to 4^+} (x-4)^2 = 0\).
What does the video imply about the existence of a two-sided limit if the one-sided limits are not equal?
-If the one-sided limits from the left and right are not equal, the two-sided limit does not exist.
What is the significance of the piecewise function in the video?
-The piecewise function is used to illustrate how limits are calculated at points where the function's definition changes.
How does the video use the signal function to demonstrate the concept of limits?
-The video uses the signal function to show that the limit as \(x\) approaches 0 does not exist because the left-hand and right-hand limits are not equal.
What is the conclusion about the limit of the piecewise function \(H(x)\) as \(x\) approaches 1?
-The conclusion is that the limit of the piecewise function \(H(x)\) as \(x\) approaches 1 exists and is equal to 3.
What is the role of the function \(f(x)\) in explaining limits near a point of discontinuity?
-The function \(f(x)\) is used to demonstrate that limits can exist at points of discontinuity if the one-sided limits are equal, even though the function is not defined at that point.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Calculus (Version #2) - 1.1 Limits Graphically
Introduction to Limits (NancyPi)

Wicked Limits! | This is how You Rock Calculus!

Calculus 1 - Introduction to Limits

Limit of a Function using a Graph - Basic/Differential Calculus

Real Analysis | Limit of Function - Concept of Limit, Left hand & Right hand Limit
5.0 / 5 (0 votes)
