Cuartiles, deciles y percentiles Definición e interpretaciones
Summary
TLDREn este video educativo, se explican los conceptos de cuantiles, cuartiles, deciles y percentiles en estadística. Los cuantiles son medidas que dividen un conjunto de datos en partes iguales. Los cuartiles dividen en cuatro partes, los deciles en diez y los percentiles en cien, cada una representando un porcentaje específico de la distribución de datos. Se utilizan ejemplos hipotéticos de sueldos para ilustrar cómo estos cuantiles pueden interpretarse y aplicarse en contextos reales, facilitando la comprensión de estas medidas estadísticas y su relevancia en la vida cotidiana.
Takeaways
- 📊 Los cuantiles son medidas que dividen un conjunto de datos en partes iguales, representando diferentes porcentajes de la distribución de datos.
- 🔢 Los cuartiles dividen los datos en cuatro partes iguales, cada una representando el 25% de la distribución, y son representados por Q1, Q2 (mediana), y Q3.
- 📈 Los deciles dividen la información en diez partes iguales, cada una representando el 10%, y son representados por D1, D2, ..., D10.
- 📉 Los percentiles dividen los datos en cien partes iguales, cada una representando el 1%, y son representados por P1, P2, ..., P99.
- ✂️ El número de cortes para dividir un conjunto de datos en partes iguales es uno menos que el número de partes, por ejemplo, tres cortes para cuatro partes.
- 💼 Un ejemplo práctico mencionado en el guion es la distribución de salarios mensuales en una empresa, utilizando cuantiles para entender la estructura salarial.
- 💡 El Q1 (primer cuartil) indica que el 25% de los trabajadores ganan menos de un cierto valor, mientras que el 75% ganan más.
- 📊 El D5 (quinto decil) es igual a la mediana, que es el punto que divide la distribución en dos partes iguales, con el 50% de los valores por debajo y el otro 50% por encima.
- 🔑 El P50 (percentil 50) también representa la mediana, mostrando que el 50% de los datos está por debajo de este valor y el otro 50% por encima.
- 📋 Los cuantiles son útiles para entender la distribución de datos y para comparar diferentes conjuntos de datos en contextos reales como la economía, la educación, etc.
Q & A
¿Qué son los cuantiles y para qué sirven?
-Los cuantiles son medidas que dividen un conjunto de datos en partes iguales, y se utilizan para organizar y analizar la distribución de los datos.
¿Cuál es la diferencia entre cuartiles, deciles y percentiles?
-Los cuartiles dividen los datos en cuatro partes iguales, los deciles en diez partes iguales y los percentiles en cien partes iguales, cada una representando un porcentaje específico de la distribución de datos.
Si un conjunto de datos se divide en cuartiles, ¿cuántos cortes se necesitan para separarlos?
-Para separar un conjunto de datos en cuartiles, se necesitan tres cortes, ya que el número de cortes es uno menos que el número de partes.
¿Qué porcentaje de la distribución de datos representa cada cuartil?
-Cada cuartil representa el 25% de la distribución de datos.
Si un percentil divide los datos en 100 partes iguales, ¿qué porcentaje representa cada una de estas partes?
-Cada parte en un percentil representa el 1% de la distribución de datos.
¿Cómo se interpreta el cuartil 1 en términos de salarios mensuales de una empresa?
-El cuartil 1 indica que el 25% de los trabajadores ganan mensualmente una cantidad menor o igual a un valor específico, en el ejemplo dado, $850.
¿Qué significa el percentil 85 en un escenario de salarios mensuales?
-El percentil 85 indica que el 85% de los trabajadores tienen sueldos menores o iguales a un valor específico, en este caso, $80.
Si el cuartil 3 supera el 75% de las observaciones, ¿qué significa eso en términos de datos?
-Significa que el 75% de los datos están por debajo del cuartil 3, y el 25% restante está por encima de este punto.
¿Cuál es la relación entre el deil 5 y la mediana?
-El deil 5 es igual a la mediana, ya que ambos dividen la información en dos partes iguales, con el 50% de los datos por debajo y el otro 50% por encima.
Si un percentil supera el 30% de las observaciones, ¿cuál es ese percentil?
-Ese percentil sería el percentil 30, ya que representa el 30% de la distribución de datos.
¿Qué percentil es igual a la mediana cuando se dividen los datos en 100 partes iguales?
-La mediana es igual al percentil 50, ya que divide la información en dos partes iguales, con el 50% de los datos por debajo y el otro 50% por encima.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

MEDIDAS DE POSICIÓN (CUARTIL, DECIL, PERCENTIL) - DATOS AGRUPADOS

Cuartiles, deciles y percentiles, datos agrupados, no agrupados, medidas de posición
MEDIDAS DE POSICIÓN: PERCENTILES, DECILES Y CUARTILES #estadistica #deciles #percentiles
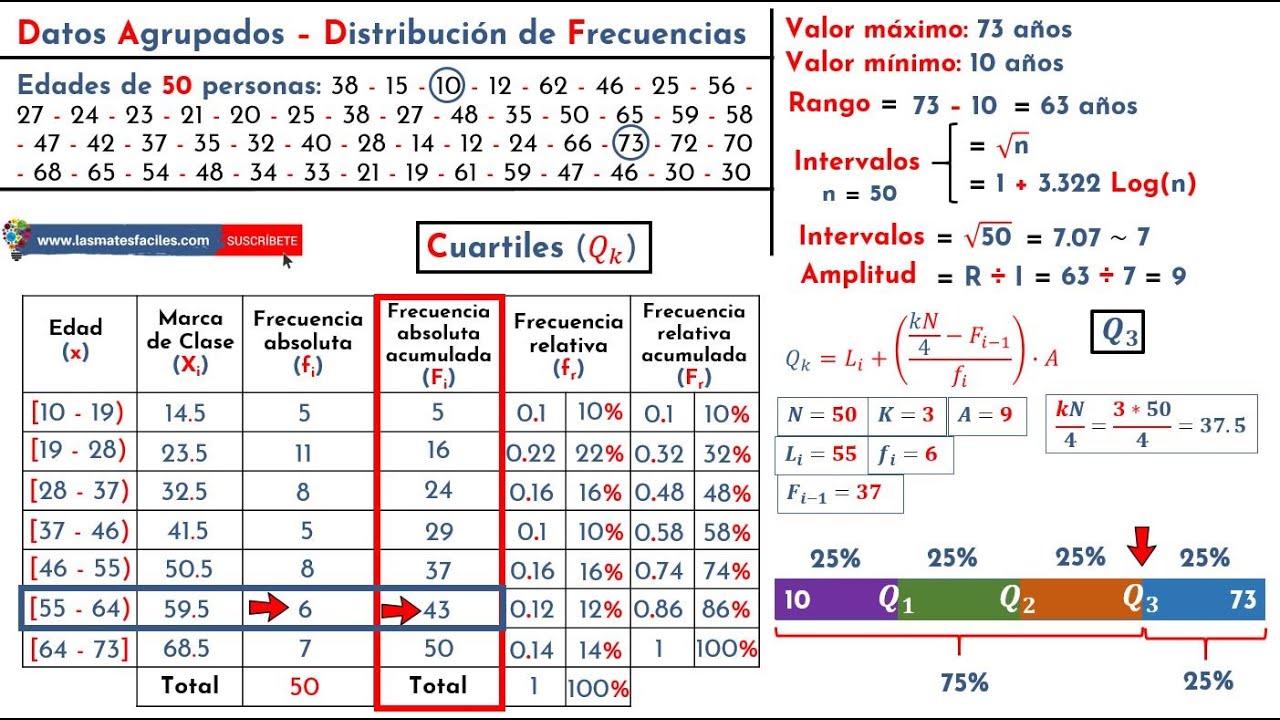
Cuartiles, Deciles y Percentiles - Datos Agrupados
Parámetros de posición: mediana, cuartiles, deciles y percentiles, estadística descriptiva

CUARTILES, DECILES Y PERCENTILES PARA DATOS NO AGRUPADOS
5.0 / 5 (0 votes)
