Algorithms Lesson 6: Big O, Big Omega, and Big Theta Notation

Summary

This lesson delves into algorithm efficiency through Big O, Big Omega, and Big Theta notations, focusing on scalability and speed relative to input size. It explains these mathematical bounds using real functions and their graphical representations, illustrating how they can limit the growth of more complex functions. The discussion transitions to their application in algorithms, particularly with integer inputs like array sizes in sorting. The lesson aims to provide a visual understanding of these bounds, with practical algorithmic examples to follow.

Takeaways

• 🔍 The lesson focuses on analyzing the efficiency of algorithms, specifically their scalability and speed, in relation to input size.
• 📏 It introduces the use of the letter 'N' to represent an unknown input size, which is a common practice in algorithm analysis.
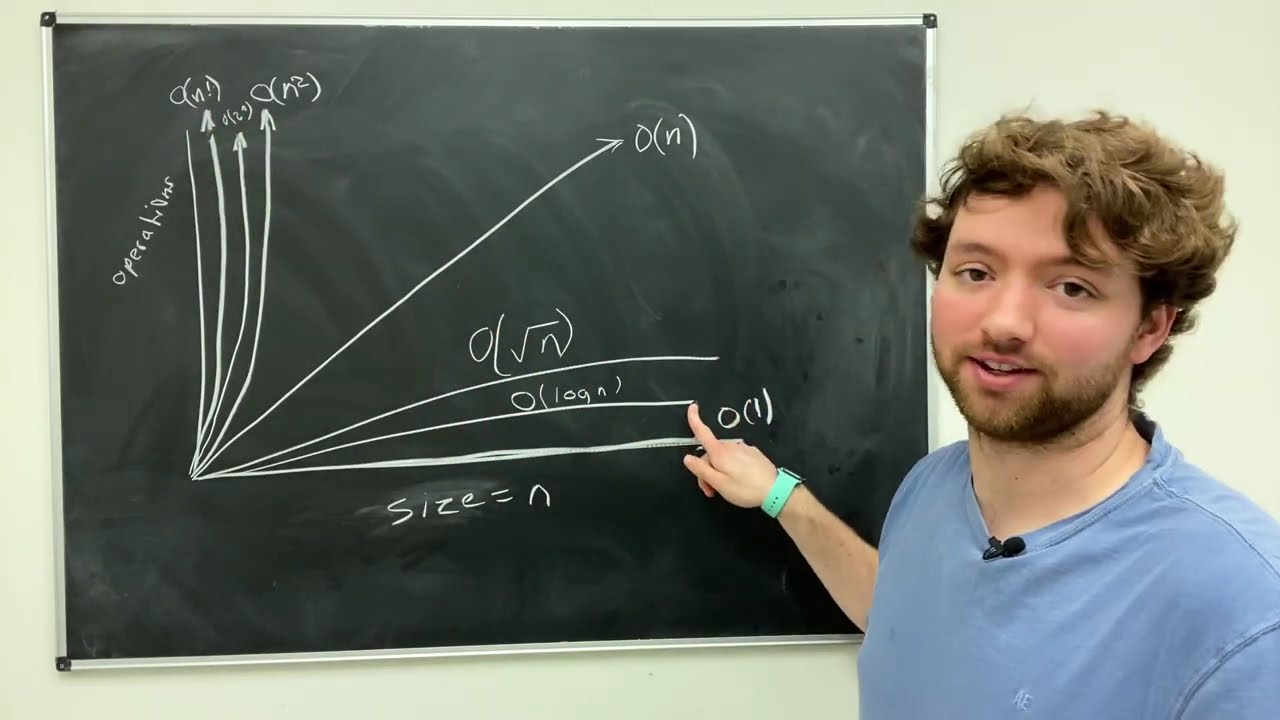
• 📊 Three types of bounds are discussed to formalize the growth of an algorithm's operations relative to input size: Big O, Big Omega, and Big Theta.
• 📈 Big O notation is used to describe an upper bound on the growth of a function, indicating that f(x) is less than or equal to C * g(x) for some constant C and for all x greater than x0.
• 📉 Big Omega notation is used for a lower bound, where f(x) is greater than or equal to C * g(x) for some constant C and for all x greater than or equal to x0.
• 🔗 Big Theta notation is used when a function is bounded both from above and below by the same function g(x), suggesting that f(x) grows at the same rate as g(x).
• 📋 The lesson provides a visual representation of these bounds using graphs to help understand how they apply to real functions and algorithms.
• 💡 The concept of bounding is crucial for understanding the scalability of algorithms when applied to large datasets.
• 🔢 The script emphasizes that these notations are used for functions defined on positive integers, which is typical for algorithm analysis where the input size is a positive integer like the size of an array.
• 📚 The lesson concludes with a promise of upcoming lessons that will provide concrete examples of these notations applied to specific algorithms.

Q & A

What is the main focus of the lesson six on algorithm efficiency?

The main focus of lesson six is to understand an algorithm's scalability, particularly its speed, in terms of the growth in the number of operations relative to the input size.

What is the input size typically referred to in the context of algorithm analysis?

In the context of algorithm analysis, the input size typically refers to the number of elements that an algorithm is processing, such as the number of elements in an array for a sorting algorithm.

What do the letters N and n commonly represent in algorithm analysis?

In algorithm analysis, the letter N is used to represent an unknown input size, while n is used to signify an integer variable, often representing the size of an array or a similar discrete structure.

What are the three types of bounds used to formalize the growth of functions in algorithm analysis?

The three types of bounds used to formalize the growth of functions in algorithm analysis are Big O (O), Big Omega (Ω), and Big Theta (Θ).

What does it mean for a function f(x) to be in Big O of G(x)?

A function f(x) is said to be in Big O of G(x) if there exist positive constants C and x0 such that f(x) is less than or equal to C * G(x) for all x greater than x0.

How is Big Omega notation used to describe the growth of a function relative to another?

Big Omega notation is used to describe the growth of a function f(x) from below relative to another function G(x), where there exist positive constants C and x0 such that f(x) is greater than or equal to C * G(x) for all x greater than or equal to x0.

What is the condition for a function f(x) to be in Big Theta of G(x)?

A function f(x) is in Big Theta of G(x) if there exist positive constants C1, C2, and x0 such that C1 * G(x) is greater than or equal to f(x) which is greater than or equal to C2 * G(x) for all x greater than or equal to x0.

Why are constants C1 and C2 different in the definition of Big Theta?

Constants C1 and C2 are different in the definition of Big Theta to indicate that the function f(x) can be bounded by G(x) from both above and below by different multiples, ensuring that f(x) grows at a rate that is asymptotically equal to G(x).

How does the concept of Big O notation help in understanding algorithm efficiency?

Big O notation helps in understanding algorithm efficiency by providing an upper bound on the growth rate of an algorithm's running time or space requirements, allowing us to classify and compare the scalability of different algorithms.

What is the significance of the white region in the graphs shown during the lesson?

The white region in the graphs represents the area where the function f(x) is bounded by the function G(x) multiplied by a constant, indicating the growth rate of f(x) relative to G(x) from a certain point onward.

Outlines

00:00

📚 Introduction to Algorithmic Complexity Notations

This paragraph introduces the concept of algorithmic efficiency and scalability, focusing on the speed of algorithms in relation to input size. It explains the use of the letter 'N' to represent unknown input size and discusses the growth in terms of 'n'. The paragraph introduces three types of bounds used to formalize growth: Big O, Big Omega, and Big Theta. These notations are mathematically defined to compare the growth of one function relative to another simpler one. The concept is illustrated with graphs of two real functions, 'f(x)' and 'g(x)', where 'f(x)' is more complex, and its growth is measured in terms of 'g(x)'. The paragraph explains Big O notation as a way to bound 'f(x)' from above by a constant multiple of 'g(x)' from some point onward, and Big Omega as bounding 'f(x)' from below. Big Theta is used when 'f(x)' is bounded both from above and below by constant multiples of 'g(x)'. The explanation is geared towards understanding how these notations apply to algorithms, particularly in terms of their operation count relative to input size.

05:01

🔍 Deep Dive into Big O, Big Omega, and Big Theta Notations

The second paragraph delves deeper into the definitions of Big O, Big Omega, and Big Theta notations, specifically in the context of algorithms and integer inputs. It clarifies that for algorithms, the input size is typically a positive integer, such as the size of an array for a sorting algorithm. The paragraph uses the notation 'F(n)' and 'G(n)' to represent functions on positive integers, which is a shift from the real variable 'x' used in mathematics. The definitions of Big O, Big Omega, and Big Theta are reiterated with examples that illustrate how a constant multiple of 'G(n)' can bound 'F(n)' from above or below from a certain point 'n0' onward. The paragraph emphasizes the visual representation of these bounds with graphs of 'F(n)' and 'G(n)' on integer values. It concludes by stating that the purpose of this explanation is to provide a visual and definitional understanding of these bounds, with the intention of applying these concepts to specific algorithms in future lessons.

Keywords

💡Algorithm Efficiency

Algorithm efficiency refers to how well an algorithm performs in terms of time and resources when processing data. In the video, efficiency is discussed in the context of scalability, which is crucial for determining how quickly an algorithm can handle large datasets. The script mentions that efficiency is measured by the growth in the number of operations relative to the input size, which is a fundamental concept for understanding the performance of algorithms.

💡Scalability

Scalability is the ability of an algorithm to handle a growing amount of work by adding resources or by efficiently coping with increased demand. The video script emphasizes scalability as a key aspect of algorithm efficiency, particularly in the context of processing large datasets. It is mentioned that understanding scalability helps in predicting how an algorithm will perform as the input size grows.

💡Input Size

Input size is the measure of the amount of data an algorithm has to process. In the script, it is typically represented by the variable N, which stands for an unknown input size. The concept is central to the discussion of algorithm efficiency because it directly relates to the number of operations an algorithm must perform, as seen in examples like linear and binary search algorithms.

💡Big O Notation

Big O notation is a mathematical concept used to describe the upper bound of an algorithm's time or space complexity. The video script explains that Big O is used to find a constant that bounds a function from above, indicating the worst-case scenario for an algorithm's performance. It is a crucial tool for analyzing and comparing the efficiency of different algorithms.

💡Big Omega Notation

Big Omega notation is used to describe the lower bound of an algorithm's performance, indicating the best-case scenario. In the video, it is mentioned as a way to bound a function from below, showing the minimum number of operations an algorithm must perform. This is important for understanding the minimum efficiency of an algorithm.

💡Big Theta Notation

Big Theta notation is used to describe the exact growth rate of an algorithm, indicating that an algorithm's performance is bounded both from above and below by a function. The script explains that if an algorithm's growth is bounded by the same constants for both Big O and Big Omega, it is in Big Theta, which means the algorithm's complexity is consistently related to the input size.

💡Growth Rate

Growth rate refers to how the running time or space requirements of an algorithm increase as the input size grows. The video script discusses growth rate in relation to Big O, Big Omega, and Big Theta notations, which are used to classify and compare the efficiency of algorithms based on their growth rate with respect to input size.

💡Constants

Constants in the context of the video refer to the fixed values used in Big O, Big Omega, and Big Theta notations to bound the growth of functions. These constants help in establishing the relationship between the complexity of an algorithm and its input size. The script mentions that these constants are crucial for formally defining the bounds of an algorithm's performance.

💡Positive Integers

Positive integers are used in the video script to represent the discrete nature of input sizes for algorithms, particularly in the context of algorithms that operate on data structures like arrays. The script explains that functions defined on positive integers, such as F(n) and G(n), help in understanding the algorithm's performance on integer inputs, which is common in computer science.

💡Function Graphs

Function graphs are visual representations of functions used in the video to illustrate the growth of algorithmic functions relative to simpler ones. The script describes how the graphs of functions f(x) and g(x) can be used to determine if one function is in Big O, Big Omega, or Big Theta of another. These visual aids help in understanding the theoretical concepts of algorithm analysis.

💡Concrete Examples

Concrete examples are practical instances of algorithms that are used in the video to demonstrate the application of Big O, Big Omega, and Big Theta notations. The script mentions that upcoming lessons will provide these examples to clarify how these notations apply to specific algorithms, helping viewers to connect the theoretical concepts with real-world scenarios.

Highlights

Introduction to algorithm efficiency and scalability in terms of speed and memory requirements.

Definition of algorithm speed in terms of the growth in the number of operations relative to input size.

Use of the letter 'N' to represent an unknown input size in algorithm analysis.

Explanation of Big O, Big Omega, and Big Theta notations as mathematical bounds to relate the growth of functions.

Graphical representation of functions f(x) and g(x) to illustrate the concept of bounding.

Formal definition of Big O notation, indicating an upper bound for a function's growth.

Formal definition of Big Omega notation, indicating a lower bound for a function's growth.

Formal definition of Big Theta notation, indicating both upper and lower bounds for a function's growth.

Discussion on the selection of constants and input size (x0) for bounding functions.

Transition from real functions to functions on positive integers for algorithm analysis.

Use of Hungarian notation and the variable 'n' to represent integer variables in algorithms.

Graphical representation of functions F(n) and G(n) on integer values.

Explanation of how to determine if a function F(n) is in Big O of G(n) using graphical analysis.

Explanation of how to determine if a function F(n) is in Big Omega of G(n) using graphical analysis.

Explanation of how to determine if a function F(n) is in Big Theta of G(n) using graphical analysis.

Purpose of the lesson to provide a visual impression and exact definition of the bounds.

Anticipation of upcoming lessons with concrete examples applying these concepts to specific algorithms.

Transcripts

[Music]

lesson six big O big Omega and big Theta

notation when we speak of an algorithm's

efficiency we want to determine its

scalability that is we want to know that

when the algorithm is applied to a large

data set that it will finish relatively

quickly we can also talk about how much

memory and algorithm requires but for

now we will focus on

speed we measure an algorithm speed in

terms of the growth in the number of

operations relative to the input size

for the linear and binary search

algorithms for example the input size is

the number of elements that we are

searching typically we will use the

letter N to represent an unknown input

size and we will talk about the growth

in terms of

n to formalize our ideas of growth there

are three types of bounds that we will

address here big O big Omega and big

Theta the definitions that we will use

come from mathematics and are used to

relate the growth in one function

relative to another simpler

one here we have the graphs of two real

functions f ofx and g ofx given by the

gray and dashed arrows which we Ed to

indicate that the functions continue

indefinitely the function f ofx is more

complex and we want to measure its

growth in terms of the simpler function

G ofx more specific specifically we want

to find a constant such that when we

multiply it by the function G ofx it

will bound the function f ofx above from

some point

onward assuming that the graph of f ofx

does not intersect the graph of C * G

ofx after the point x0 we know that the

graph of f ofx remains in this white

region for all x to the right of

x0 in this case we say that f ofx is in

Big O of G ofx formally we say that f

ofx is in Big O of G ofx if there exist

positive constants C and x0 such that f

ofx is less than or equal to C * G ofx

for all X greater than

x0 on the other hand we could bound the

function f ofx From Below like this if

such a constant exists such that c * G

ofx bounce F ofx below from some point

onward then we say that f ofx is in big

Omega of G ofx formally f ofx is in big

Omega of G ofx if there exist positive

constants C and x0 such that f ofx is

greater than or equal to C * G ofx for

all X greater than or equal to

x0 if there are constants such that g

ofx bounds the function f ofx both from

below and above then we say that f ofx

is in big Theta of G ofx X of course the

constants in this case are different so

we have labeled them C1 and C2 to

clarify that the x0 that we choose can

be any value that is far enough out that

F ofx doesn't intersect either C1 * G of

X or C2 * G ofx anymore and remains in

this white area forly we say that f ofx

is in big Theta of G ofx if there exist

positive constants C1 C2 and x0 such as

that C1 * G ofx is greater than or equal

to F ofx which is greater than or equal

to C2 * G ofx for all X greater than or

equal to

x0 so far we have shown what the

situation looks like for General real

functions for algorithms the input size

is generally a positive integer like the

size of an array for a sorting algorithm

in this case we can think of our f and g

as functions on the positive

integers in mathematics X is used to

signify a real variable while n is used

to signify an integer variable like

Hungarian notation and programming this

notation allows us to see more

immediately what is going on so we will

use

it using this notation here we see the

graphs of two example functions F of N

and G of n given by the solid gray and

Hollow black dots respectively notice

that the graphs are made up of single

dots instead of Curves this is because

the functions are are defined on Integer

values just as we had for the real

functions we can have constants such

that when we multiply G of n by them we

bound F of n from some point onward and

the definitions are

analogous here we have a constant

multiple of G of n such that its graph

is above the graph of f of n from some

point onward the last value that puts

the graph below the graph of f ofn is

2 so we can set n0 to 3 and we have F

ofn in the white areas below the graph

of C * G of n from 3 onward this is how

we Define Big O of G of n forly we say

that f ofn is in Big O of G of n if

there exists a positive real number c

and a positive integer n0 such that F of

n is less than or equal to C * G of n

for all integers n greater than or equal

to

n0 likewise we might have a constant

multiple of a function G of n such that

c * G of n bounds F of n below from some

point n0 onward in this case f ofn is

said to be in big Omega of G of n

formally we say that f ofn is in big

Omega of G of n if there exists a

positive constant c and a positive

integer n0 such that F of n is greater

than or equal to C * G of n for all n

greater than or equal to

n0 additionally we can have two constant

multiples of G of of n that bound the

function f of n on both sides from some

point n0 onward here again we say that F

of n is in big Theta of G of n formally

we see that F of n is in big Theta of G

of n if there exist positive constants

C1 and C2 and a positive integer n0 such

that C1 * G of n is greater than or

equal to F ofn which is greater than or

equal to C2 * G of n for all n greater

than or equal to n0

our purpose at this point is simply to

give a visual impression of these bounds

along with an exact definition in the

coming lessons we will give concrete

examples of how they apply to specific

algorithms so that these ideas become

clear this concludes the lesson