Number System grade 10
Summary
TLDRThis educational video lesson focuses on teaching interval notation, set builder notation, and number lines, which are often challenging for students. The instructor uses a step-by-step approach to explain how to represent numbers greater than three and less than seven on a number line, employing open circles to denote exclusion of the endpoints. The lesson covers interval notation with parentheses to indicate non-inclusive boundaries and set builder notation using brackets to specify conditions for variables. The instructor also introduces the concept of real numbers and infinity, using creative analogies like a hungry crocodile to help students remember the direction of inequalities. The lesson aims to demystify these mathematical concepts through practice and repetition.
Takeaways
- 📚 The lesson introduces interval notation, set builder notation, and number lines, which are often challenging for students.
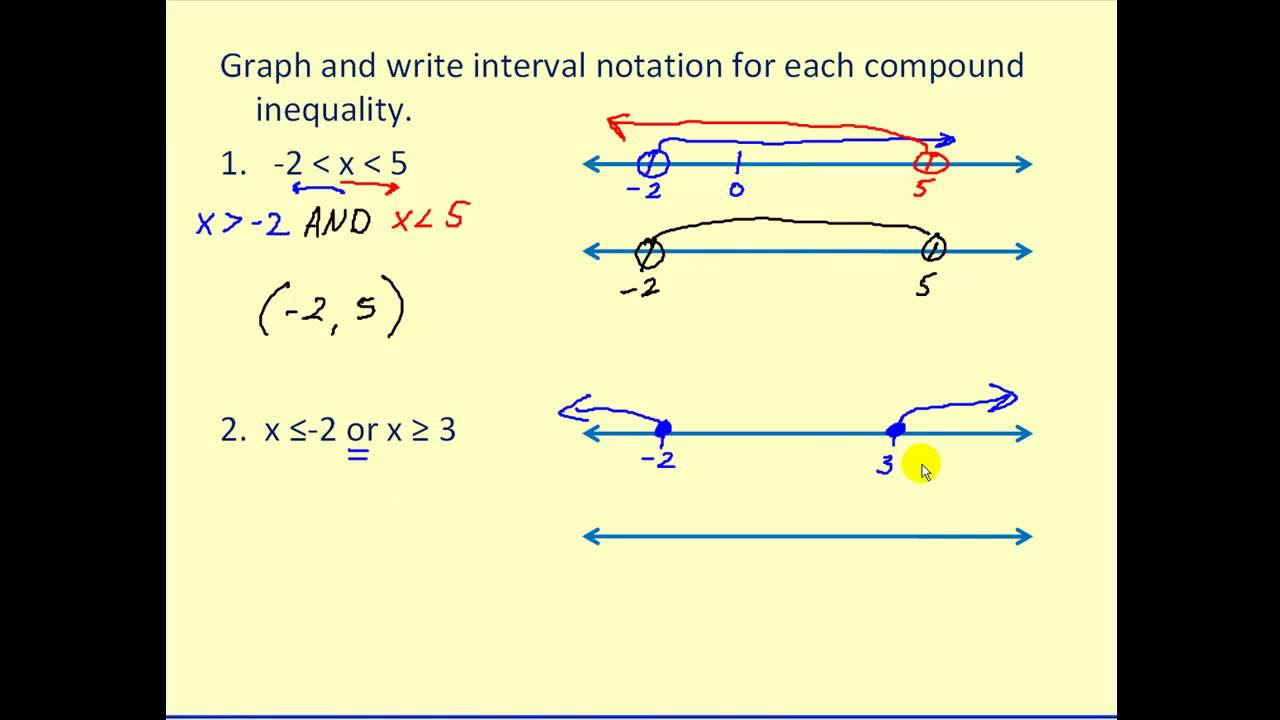
- 🔢 It explains how to represent numbers greater than three and less than seven, including examples like 3.1, 4.2, 5.6, and 6.54.
- 📏 The number line is used to visualize intervals, with open circles indicating numbers not included (e.g., 3 and 7).
- 📝 Interval notation is introduced as a concise way to express ranges, using round brackets to denote non-inclusive endpoints.
- 🦎 A mnemonic is used to remember the notation: a 'hungry crocodile' facing the larger number signifies 'greater than' or 'less than'.
- 📋 Set builder notation is explained, using specific brackets and the letter 'x' to define the set of numbers that meet certain conditions.
- 🌐 The concept of real numbers is briefly touched upon, indicating that 'x e r' signifies 'x is an element of the real numbers'.
- 🔄 The lesson reiterates the importance of practice to understand and apply these mathematical notations effectively.
- 🔄 The instructor provides another example with numbers greater than or equal to 7 and less than 12, demonstrating how to adjust the notation accordingly.
- ♾️ The lesson concludes with an example of numbers greater than five, introducing the concept of infinity in interval notation.
Q & A
What are the three different ways to represent numbers between 3 and 7 in mathematics?
-The three different ways to represent numbers between 3 and 7 are using a number line with open circles at 3 and 7, interval notation (x e [3,7)), and set-builder notation (x ∈ ℝ | 3 < x < 7).
What does the open circle on a number line represent?
-An open circle on a number line indicates that the number at that point is not included in the set.
How do you represent numbers that are not included in the set using interval notation?
-In interval notation, numbers that are not included in the set are represented with round brackets, for example, (3,7).
What does 'x e' stand for in interval notation?
-In interval notation, 'x e' is an abbreviation for 'x is an element of', indicating that x belongs to the set described within the brackets.
What is set-builder notation and how is it used to describe numbers between 3 and 7?
-Set-builder notation is a way to describe a set of numbers using a variable, a condition, and a colon. For numbers between 3 and 7, it would be written as {x | 3 < x < 7}.
What does 'x ∈ ℝ' mean in set-builder notation?
-'x ∈ ℝ' in set-builder notation means that x is an element of the set of real numbers, indicating that x can be any real number that satisfies the given condition.
How do you represent a number that is bigger than 5 but not including 5 on a number line?
-On a number line, a number that is bigger than 5 but not including 5 would be represented with an open circle at 5 and a continuous arrow extending to the right.
What is the interval notation for numbers that are bigger than 5 but not including 5?
-The interval notation for numbers that are bigger than 5 but not including 5 is (5, ∞).
How do you represent numbers that are bigger than 5 using set-builder notation?
-In set-builder notation, numbers that are bigger than 5 would be represented as {x ∈ ℝ | x > 5}.
Why is it important to practice these different notations for representing numbers?
-Practicing different notations helps to solidify understanding of how to represent sets of numbers mathematically and can be useful in various mathematical contexts and problem-solving.
What is the significance of the direction of the inequality symbols in set-builder notation?
-The direction of the inequality symbols in set-builder notation indicates whether the boundary numbers are included or excluded. For example, '>' means the number is strictly greater, excluding the boundary, while '≥' would include the boundary number.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführen5.0 / 5 (0 votes)