Matematika SMA - Trigonometri (1) - Pengenalan Trigonometri, Perbandingan Trigonometri (A)
Summary
TLDRThis educational video offers an in-depth exploration of trigonometry, focusing on the relationships between the sides and angles in triangles. The instructor explains fundamental trigonometric functions like sine, cosine, and tangent, and their applications in solving problems involving right-angled triangles. The video also introduces special angles and how to memorize their sine and cosine values using simple tricks. Through examples and step-by-step explanations, viewers learn how to calculate the trigonometric ratios and apply them in various scenarios. The video concludes with practice problems to reinforce the concepts.
Takeaways
- 📚 Trigonometry is the study of relationships between the sides and angles in triangles, focusing primarily on right-angled triangles.
- 🔢 The primary trigonometric ratios introduced are sine (sin), cosine (cos), and tangent (tan), each representing a ratio between different sides of a right triangle.
- 🧮 Sine (sin) is the ratio of the length of the opposite side to the hypotenuse. Cosine (cos) is the ratio of the adjacent side to the hypotenuse. Tangent (tan) is the ratio of the opposite side to the adjacent side.
- 🔄 The reciprocal trigonometric functions are cosecant (csc), secant (sec), and cotangent (cot), which are the inverses of sine, cosine, and tangent respectively.
- 🔺 The script uses an example triangle ABC with specific side lengths to demonstrate how to calculate the values of sine, cosine, and tangent using the sides of the triangle.
- 📝 The video explains how to determine the sine, cosine, and tangent values using a given angle and how to calculate unknown side lengths using the Pythagorean theorem.
- 📐 Special angles like 30°, 45°, 60°, and 90° are highlighted as important for solving trigonometry problems, with their sine, cosine, and tangent values provided in a table.
- 🔢 A mnemonic is provided to help memorize the sine values of these special angles, using the pattern of multiplying by 1/2 and taking the square root.
- 📏 The video also explains how to calculate more complex trigonometric expressions involving multiple operations and special angles.
- 📊 The script emphasizes the importance of understanding and memorizing key trigonometric values and relationships to solve problems effectively.
Q & A
What is trigonometry?
-Trigonometry is the study of the relationships between the sides and angles in a triangle.
What are the primary trigonometric ratios?
-The primary trigonometric ratios are sine (sin), cosine (cos), and tangent (tan).
How is the sine of an angle calculated in a right triangle?
-The sine of an angle is calculated by dividing the length of the side opposite the angle by the length of the hypotenuse.
What is the formula to calculate cosine?
-Cosine is calculated by dividing the length of the adjacent side by the length of the hypotenuse.
How do you find the tangent of an angle?
-The tangent of an angle is found by dividing the length of the side opposite the angle by the length of the adjacent side.
What are cosecant, secant, and cotangent?
-Cosecant, secant, and cotangent are the reciprocals of sine, cosine, and tangent, respectively.
How do you determine the sides of a right triangle when given an angle and one side length?
-You can use trigonometric ratios, such as sine, cosine, and tangent, along with the given angle and side length, to determine the other sides.
What are special angles in trigonometry?
-Special angles are angles like 0°, 30°, 45°, 60°, and 90°, which have specific trigonometric values that are often memorized.
How can you remember the trigonometric values of special angles?
-You can remember the trigonometric values of special angles by memorizing the sine values, which then help you deduce the cosine and tangent values.
What is the Pythagorean theorem used for in trigonometry?
-The Pythagorean theorem is used to calculate the length of a side in a right triangle when the lengths of the other two sides are known.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
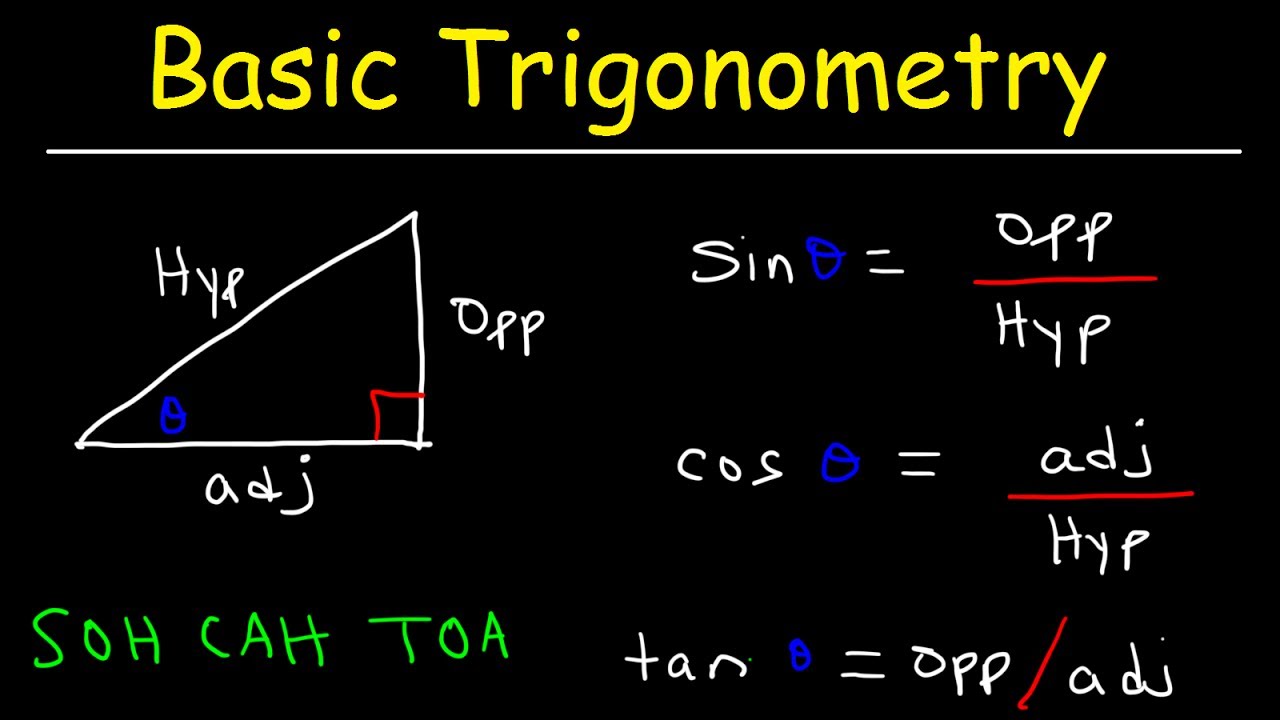
Trigonometry For Beginners!

cos(x+y)=cosx cosy-sinx siny | cos(x+y)=cosx cosy-sinx siny derivation | Trigonometry formula proof

Trigonometry made easy

TRIGONOMETRI - Ukuran Sudut dan Perbandingan Trigonometri
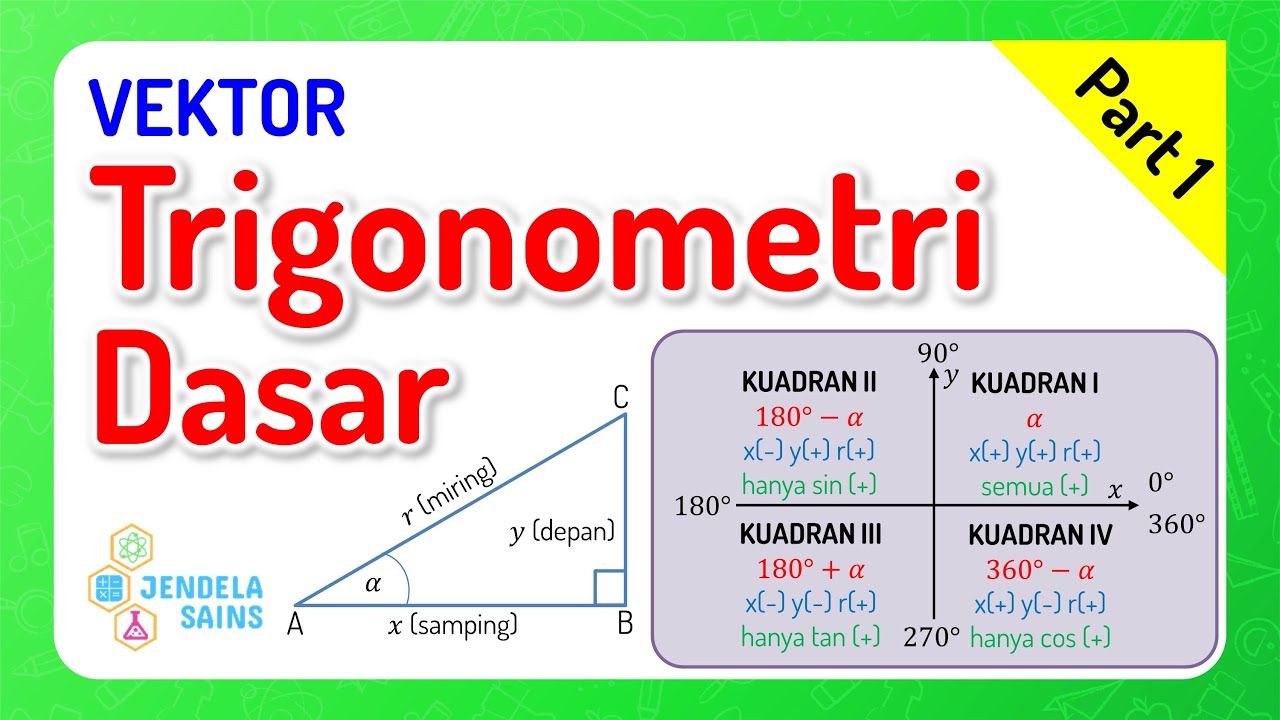
Vektor Fisika • Part 1: Pengantar Trigonometri Dasar

Matematika SMA - Trigonometri (7) - Trigonometri Aturan Sinus dan Cosinus (A)
5.0 / 5 (0 votes)
