Productos Notables | Fórmulas y Ejemplos
Summary
TLDREl script ofrece una lección sobre los productos notables en álgebra, enfocándose en fórmulas comunes como el binomio cuadrado, binomio cúbico y productos de binomios conjugados. Se describen las fórmulas para resolver expresiones algebraicas como (a + b)^2, (a - b)^2, (a + b)^3 y (a - b)^3, así como productos de binomios por trinomios. Se ilustran con ejemplos prácticos para aplicar estas fórmulas, enseñando a los estudiantes a reconocer patrones y calcular resultados eficientemente.
Takeaways
- 📚 Los productos notables son fórmulas matemáticas que siguen un patrón específico y son fáciles de recordar.
- 🔢 El primer producto notable es a^2 + 2ab + b^2, que se refiere a la suma de dos términos elevados al cuadrado.
- 📐 El segundo producto notable es a^2 - 2ab + b^2, que es similar al primero pero con una resta, y resulta en la suma de dos cuadrados.
- 📘 La fórmula de un binomio al cubo (a^3 + 3a^2b + 3ab^2 + b^3) genera cuatro términos y se utiliza para el producto de un binomio por sí mismo elevado a la tercera potencia.
- 📙 La fórmula de un binomio al cubo con resta (a^3 - 3a^2b + 3ab^2 - b^3) también genera cuatro términos pero con signos alternados.
- 🎓 El producto de binomios conjugados ((a - b)(a + b)) resulta en a^2 - b^2, que es la diferencia de los cuadrados de a y b.
- 📒 Los productos de binomios por trinomios tienen fórmulas específicas que dependen de si los términos son sumados o restados.
- 📕 Se pueden resolver ejemplos aplicando estas fórmulas de productos notables, como se muestra en el script con casos de x^3 y otros.
- 📖 El script proporciona ejemplos prácticos para ilustrar cómo se aplican las fórmulas de productos notables en cálculos algebraicos.
- 📔 Es importante observar la expresión algebraica y reconocer a qué patrón de producto notable se asemeja para aplicar la fórmula correcta.
- 📝 Se recomienda memorizar estas fórmulas de productos notables para su rápida aplicación en problemas algebraicos.
Q & A
¿Qué son los productos notables en álgebra?
-Los productos notables son expresiones algebraicas que siguen un patrón particular y son fácilmente reconocibles, como el binomio de suma y el binomio de resta, entre otros.
¿Cuál es la fórmula para el primer producto notable mencionado en el script, donde se elevan dos términos al cuadrado?
-La fórmula para el primer producto notable es \( a^2 + 2ab + b^2 \), que representa la suma de dos términos elevados al cuadrado.
¿Cómo se calcula el producto de un binomio de suma y un binomio de resta?
-El producto de un binomio de suma y un binomio de resta se calcula como \( (a + b)(a - b) = a^2 - b^2 \), que es la diferencia de los cuadrados.
¿Cuántos términos genera el producto de un binomio al cubo?
-El producto de un binomio al cubo genera cuatro términos, siguiendo la fórmula \( a^3 + 3a^2b + 3ab^2 + b^3 \).
¿Cómo se intercalan los signos en el producto de un binomio al cubo cuando se trata de una resta?
-En el producto de un binomio al cubo con resta, los signos se intercalan como negativo, positivo, negativo, positivo, siguiendo la fórmula \( a^3 - 3a^2b + 3ab^2 - b^3 \).
¿Qué se llama el producto de dos binomios que tienen el mismo primer término pero términos secundarios diferentes?
-Ese producto se llama trinomio resultante, y su fórmula es \( a^2 + ab + b^2 \) cuando los términos son \( (a + b)(a + c) \) y los segundos términos son diferentes.
¿Cómo se calcula el producto de dos binomios conjugados?
-El producto de dos binomios conjugados se calcula como \( (a + b)(a - b) = a^2 - b^2 \), que es igual a la diferencia de los cuadrados.
¿Qué es la suma de cubos y cómo se calcula?
-La suma de cubos es un producto notable que se calcula como \( a^3 + b^3 \), donde se elevan al cubo los términos del binomio y se suman los resultados.
¿Cómo se resuelve el ejemplo del script donde se calcula (2x - y)^3?
-Para resolver \( (2x - y)^3 \), se eleva al cubo cada término del binomio, se aplican las leyes de los exponentes y se siguen las fórmulas de productos notables, obteniendo un resultado de \( 8x^3 - 12x^2y^2 + 6xy^4 - y^6 \).
¿Cómo se identifica un producto notable de un binomio por un trinomio?
-Se identifica un producto notable de un binomio por un trinomio cuando el primer término del binomio es igual al primer término del trinomio, y los segundos términos pueden ser diferentes, siguiendo las fórmulas de suma de cubos si el signo intermedio es positivo.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

PRODUCTOS NOTABLES: Suma y resta de un binomio al cuadrado. Producto de dos binomios conjugados

PRODUCTOS NOTABLES desde cero

Matemáticas I: Video 2 7 1
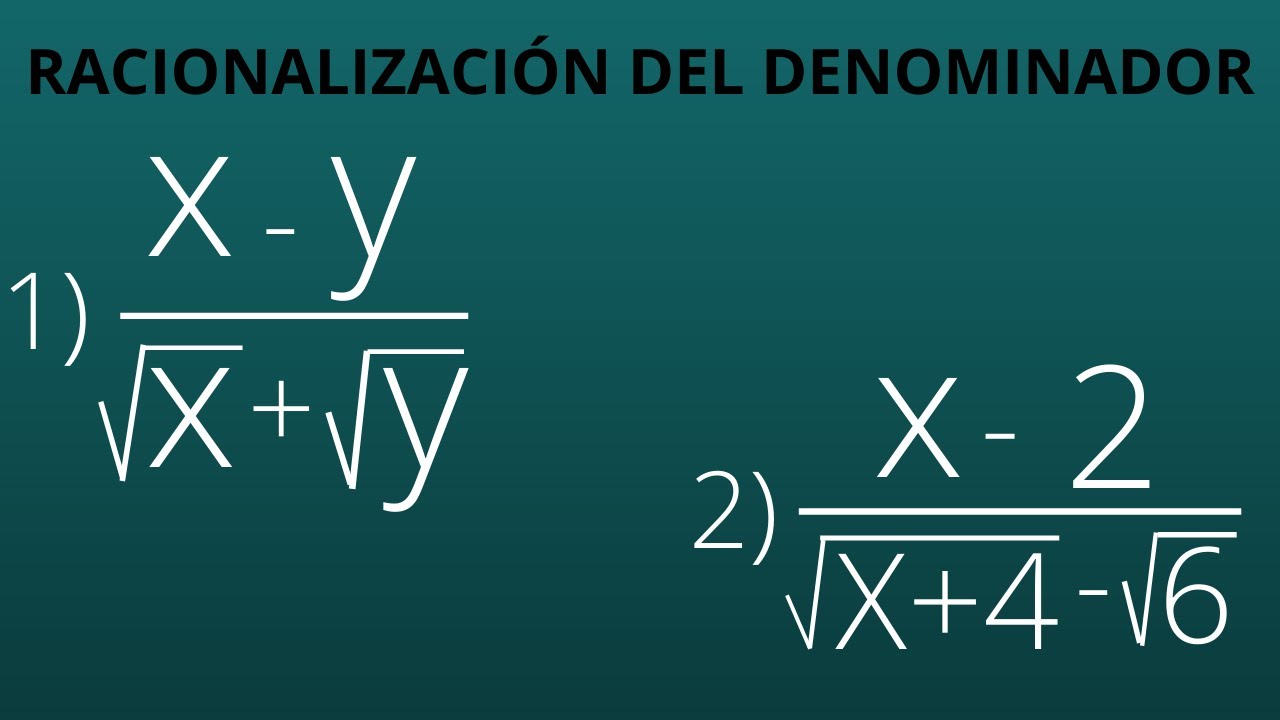
Racionalización del denominador (binomio) con expresiones algebraicas, explicado paso a paso.

Producto de binomios conjugados | Ejemplo 1 Principiantes

Productos Notables. Binomio al Cuadrado.
5.0 / 5 (0 votes)
