Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximations
Summary
TLDRThe script explores a fascinating pattern involving prime numbers and their distribution visualized in polar coordinates, leading to intriguing spirals and patterns. It delves into number theory, revealing connections between prime distribution and rational approximations of pi. The exploration of these patterns, initiated by a playful approach to data visualization, uncovers deep mathematical concepts such as Dirichlet's theorem, Euler's totient function, and the importance of co-prime numbers in understanding prime distribution. The script highlights the beauty of mathematical discovery through curiosity-driven exploration.
Takeaways
- 📊 The script discusses a unique pattern involving prime numbers and polar coordinates, which was initially presented on Math Stack Exchange by a user named Dwymark and answered by Greg Martin.
- 📍 It explains the concept of polar coordinates, where points are defined by a radius (r) and an angle (theta), measured in radians, rather than the traditional Cartesian coordinates (x, y).
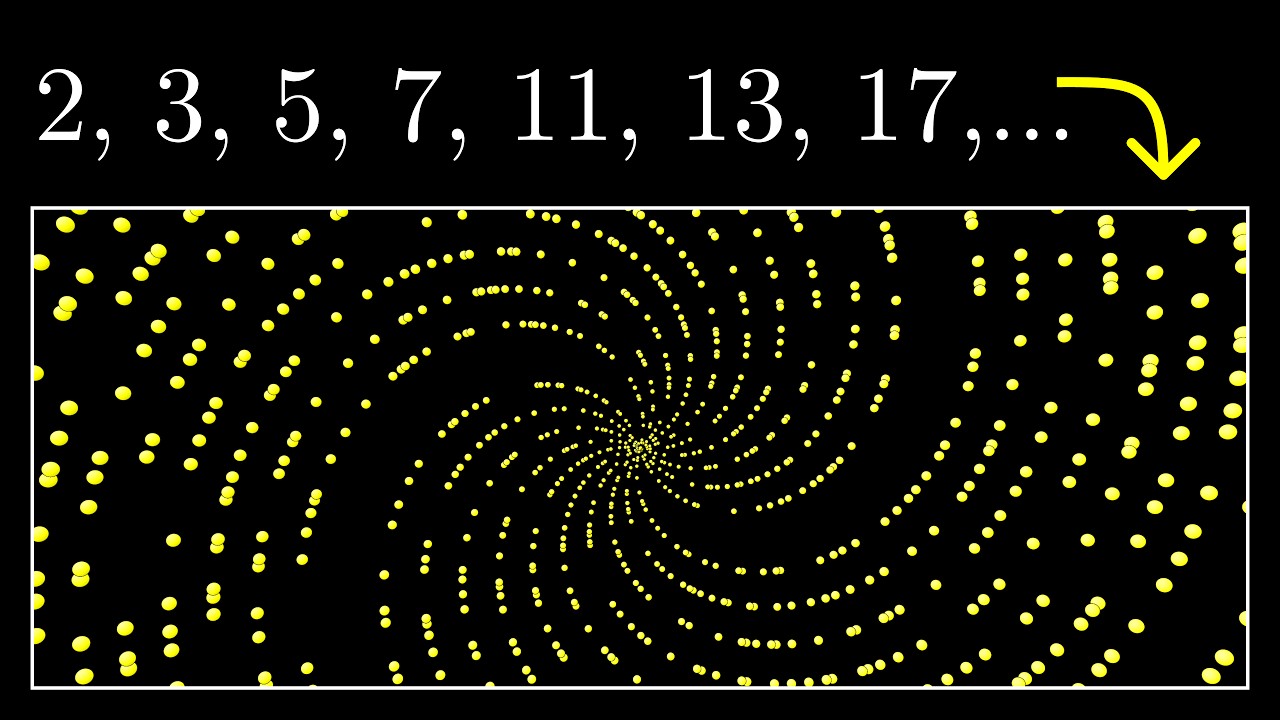
- 🌀 The pattern observed involves plotting points where both the radius and angle are prime numbers, resulting in an Archimedean spiral that reveals interesting properties when zoomed out.
- 🌌 Upon zooming out, the spirals form a galactic pattern with some 'missing arms', which upon further investigation, are found to be related to the distribution of prime numbers and not unique to them.
- 🔍 The script delves into the idea that the spirals are not a result of prime numbers specifically, but rather a feature of the way numbers increment in polar coordinates, as demonstrated by plotting all whole numbers.
- 📉 The concept of 'residue classes mod 6' is introduced to explain the smaller spirals, where multiples of 6 form one arm of the spiral, and other numbers form additional arms based on their relationship to multiples of 6.
- 🔢 The script touches on the theorem of Dirichlet, which is a fundamental theorem in number theory regarding the distribution of prime numbers, particularly in relation to residue classes.
- 🎓 Euler's totient function (phi) is mentioned, which counts the number of integers co-prime to a given number, and is used to explain the distribution of primes within residue classes.
- 🔍 The larger spirals and straight lines observed are related to the close rational approximations of pi, such as 22/7 and 355/113, and how these approximations create the visual patterns when plotting points.
- 📚 Dirichlet's theorem is further explained, stating that the primes are evenly distributed among allowable residue classes, which is a non-obvious fact proven using complex analysis.
- 🌟 The script concludes by emphasizing the value of exploratory learning in mathematics, suggesting that even arbitrary explorations can lead to deep and important mathematical insights.
Q & A
What is the significance of polar coordinates in the context of the script?
-Polar coordinates are used to label points in 2D space with a distance from the origin (radius, r) and an angle (theta) with the horizontal. In the script, they are used to visualize the pattern formed by plotting points where both coordinates are prime numbers, leading to the exploration of prime distribution and its visual representation.
What is an Archimedean spiral, and how does it relate to the script's discussion on prime numbers?
-An Archimedean spiral is a spiral formed by the locus of points corresponding to a constant increase in the angle and a linear increase in the radius. In the script, plotting points with both coordinates as prime numbers results in a spiral pattern, which is then analyzed for its relation to the distribution of prime numbers.
Why do some arms of the spiral seem to be missing when prime numbers are plotted?
-Some arms of the spiral are missing because prime numbers cannot be multiples of 6 or certain other numbers that form the arms of the spiral. This is due to the properties of prime numbers and their divisibility rules, which exclude them from forming certain patterns in polar coordinates.
What is the connection between the number of spirals and the number of rays in the script's discussion?
-The connection lies in the residue classes mod 6 and mod 44. There are 20 spirals when considering multiples of 6, and 280 rays when considering multiples of 44. These numbers arise from the fact that 44 is close to 2 pi, and turning 44 radians is almost a full turn, leading to distinct patterns in the visualization.
How does the script explain the transition from spirals to straight lines at a larger scale?
-At a larger scale, the script explains that the transition from spirals to straight lines is due to the close approximation of certain numbers to multiples of 2 pi. For example, 710 radians is extremely close to a whole number of full turns, which results in the points aligning almost exactly on straight lines.
What is Euler's totient function, and how is it mentioned in the script?
-Euler's totient function, denoted by the Greek letter phi, counts the number of integers up to a given number n that are co-prime to n. In the script, it is mentioned as a way to explain the number of allowable residue classes for prime numbers, such as phi(44) being 20.
What is Dirichlet's theorem, and how does it relate to the script's exploration of prime numbers?
-Dirichlet's theorem states that for any two co-prime integers m and n, there are infinitely many prime numbers in the arithmetic progression of the form 4n + r, where r is an integer co-prime to m. The script relates this theorem to the distribution of prime numbers in residue classes, illustrating how primes are evenly distributed among these classes.
Why does the script mention complex analysis in the context of prime number distribution?
-Complex analysis is mentioned because it is a fundamental tool used in the proof of Dirichlet's theorem, which is central to understanding the distribution of prime numbers. Despite the seemingly unrelated nature of complex numbers to the discrete set of prime numbers, this field of mathematics provides the necessary framework for such proofs.
What is the significance of the number 710 in the script's discussion of prime number distribution?
-The number 710 is significant because it is a factor of 2 pi, resulting in a very close rational approximation for 2 pi when divided by 113. This leads to a pattern in the visualization where points plotted with a radius of 710 form almost straight lines, illustrating the quality of the approximation.
How does the script use the concept of 'totitives' to explain the distribution of prime numbers?
-The script introduces 'totitives' as an alternative term for the numbers that are co-prime to a given number n, which are counted by Euler's totient function. This concept is used to explain the distribution of prime numbers among residue classes, highlighting the even spread of primes in these classes as predicted by Dirichlet's theorem.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximations

Doodling in Math: Spirals, Fibonacci, and Being a Plant [1 of 3]

studying patterns in prime numbers using a new method -- part one --

Matematika SMA - Trigonometri (6) - Koordinat Polar, Koordinat Kutub dan Kartesius (A)

MATHEMATICS IN NATURE PROVES INTELLIGENT DESIGN

Beginilah Cara Kerja Garis Di Peta Dalam Membaca Iklim!!!
5.0 / 5 (0 votes)
