Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximations
Summary
TLDRThis script explores the intriguing patterns that emerge when plotting prime numbers in polar coordinates, revealing spirals and rays that hint at a hidden order within the chaotic distribution of primes. It delves into the connection between these visual patterns and number theory, particularly Euler's totient function and Dirichlet's theorem, which describes the even distribution of primes across residue classes. The script highlights the beauty of mathematical exploration, leading from playful visualization to profound theorems, and underscores the relevance of complex analysis in understanding prime distribution.
Takeaways
- 📊 The script discusses a unique pattern observed by plotting prime numbers in polar coordinates, which results in spirals and rays.
- 🌀 The initial visual pattern is an Archimedean spiral formed by plotting points where both the radius and angle are prime numbers.
- 🔍 Upon zooming out, the spirals give way to a pattern of outward-pointing rays, some missing, resembling a comb with missing teeth.
- 🤔 The script raises questions about the origins of these patterns and their connection to the distribution of prime numbers.
- 🧩 It is revealed that similar spiral patterns appear when plotting all whole numbers, not just primes, suggesting the patterns are separate from the primes themselves.
- 📚 The script introduces mathematical concepts like polar coordinates, residue classes, and Euler's totient function to explain the observed patterns.
- 🔢 The pattern of rays and spirals is related to the number of steps taken (e.g., 6, 44, 710) and their proximity to whole rotations, which is connected to rational approximations of pi.
- 📉 The script explains that the gaps in the larger-scale pattern occur because certain residue classes mod 44 and 710 do not contain prime numbers.
- 🎓 Dirichlet's theorem is highlighted as a key theorem in number theory that explains the distribution of primes among residue classes.
- 📈 The script uses histograms to illustrate the even distribution of prime numbers among allowable residue classes as an example of Dirichlet's theorem.
- 🎨 The importance of exploring mathematical concepts through data visualization and the potential for such explorations to lead to deep mathematical insights is emphasized.
Please replace the link and try again.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
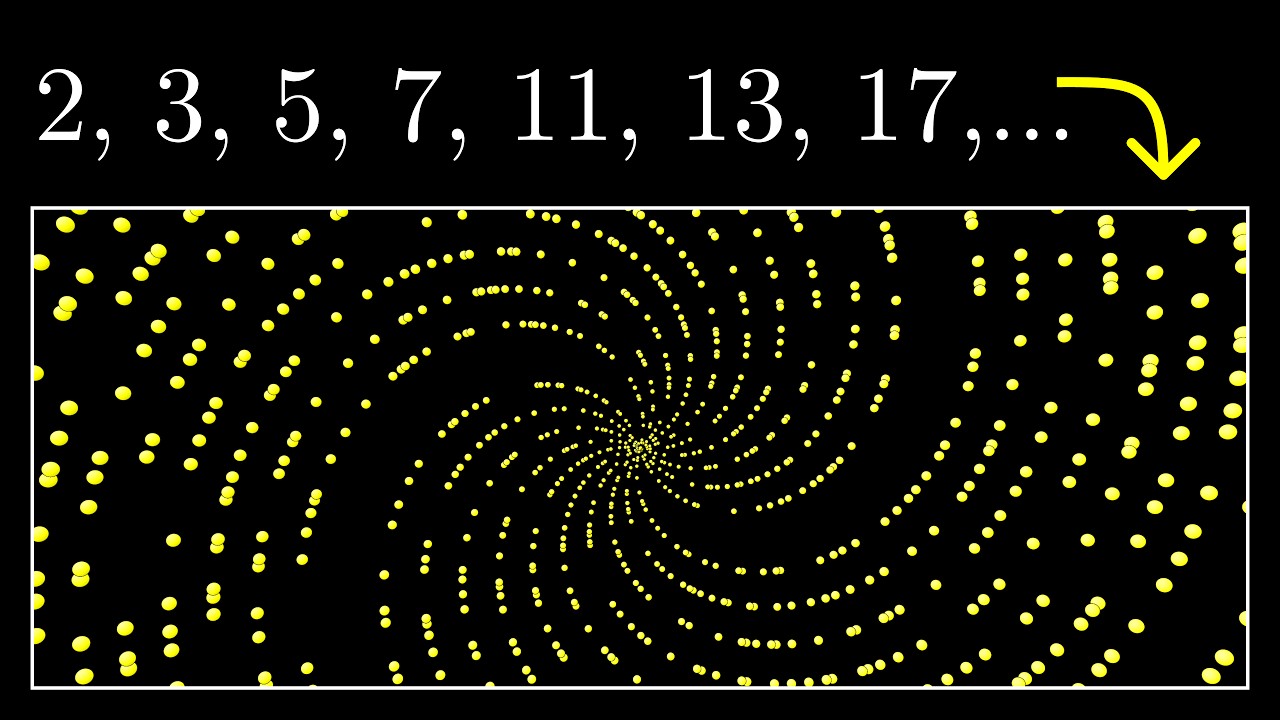
Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximations
What is Riemann Hypothesis | AH Documentary

Doodling in Math: Spirals, Fibonacci, and Being a Plant [1 of 3]

You can only breathe if the timer is prime.

Prime numbers | Factors and multiples | Pre-Algebra | Khan Academy

How Are Prime Numbers Used In Cryptography?
5.0 / 5 (0 votes)