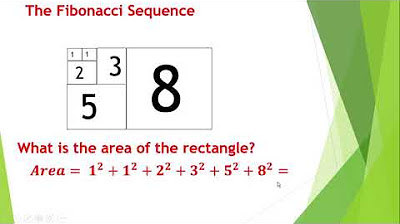NATURES MATHEMATICS PART-1 1080p HD DOCUMENTARY
Summary
TLDRThis script delves into the fascinating intersection of mathematics and nature, highlighting the prevalence of the Fibonacci sequence and the golden ratio in natural phenomena. It explores how these mathematical concepts manifest in the arrangement of seeds in sunflowers, the spirals of shells, and the patterns on animals. The script also touches on the work of Alan Turing in explaining animal markings and the role of geometrical configurations in creating natural optical phenomena like rainbows and glories, emphasizing the beauty and wonder of mathematics in the world around us.
Takeaways
- 🧠 Mathematics is considered by some to be discovered rather than invented, with philosophical presuppositions influencing this view.
- 📚 Fibonacci, a 12th-century mathematician, is known for the Fibonacci sequence, which is prevalent in nature and follows a pattern where each number is the sum of the two preceding ones.
- 🌻 The Fibonacci sequence appears in the arrangement of seeds on a sunflower, with the numbers of seeds in clockwise and anti-clockwise spirals often being consecutive Fibonacci numbers.
- 🔢 The golden ratio, approximately 1.618, emerges from the Fibonacci sequence as the ratio of successive numbers converges towards this value, and it has significance in geometry and nature.
- 📐 The golden angle, derived from the golden ratio, is about 137.5 degrees and is observed in the arrangement of leaves on a stem, optimizing sunlight exposure.
- 🌵 The Fibonacci sequence and golden ratio are also seen in the growth patterns of plants like cacti, where leaves grow at the golden angle to each other.
- 🐆 Alan Turing's work on morphogenesis explains the chemical basis for patterns on animals, such as spots and stripes, through the interaction of chemical pigments.
- 🌈 Iridescent colors in nature, seen in birds and insects, are not due to pigments but to microscopic structures that split sunlight into its component colors.
- 🌦️ Rainbows are a result of sunlight interacting with raindrops under specific conditions, demonstrating subtle geometric principles.
- ✈️ Glories, observed from an airplane, are circular colored rings caused by backscattering of light by cloud droplets, with smaller droplets creating larger glories.
- 🌐 Atmospheric optical phenomena, such as sun halos and sundogs, involve interactions between sunlight and water or ice crystals, highlighting the importance of geometrical configurations.
Q & A
What is the philosophical debate surrounding the nature of mathematics?
-The debate is whether mathematics is something humans invent or discover. This perspective can influence the conclusions one draws about its role and usefulness in understanding the world.
Who is Fibonacci and what is his significant contribution to mathematics?
-Fibonacci was a twelfth-century mathematician from Pisa, Italy. He is known for the Fibonacci sequence, a series of numbers where each number is the sum of the two preceding ones, which appears frequently in nature.
What is the Fibonacci sequence and how does it manifest in nature?
-The Fibonacci sequence is a series starting with 1, 1, followed by each number being the sum of the two preceding ones (e.g., 2, 3, 5, 8, 13, etc.). It appears in various natural phenomena such as the arrangement of seeds in a sunflower and the spiral patterns in shells.
What is the Golden Ratio and how is it related to the Fibonacci sequence?
-The Golden Ratio, approximately 1.618, is a special value that appears as the ratio of successive Fibonacci numbers converges. It is derived from the geometry of a regular pentagon and is found in various natural structures and designs.
What is the significance of the Golden Angle in nature?
-The Golden Angle, approximately 137.5 degrees, is often found in the arrangement of leaves on a stem, which allows for optimal sunlight exposure. It is related to the Golden Ratio and contributes to the efficient packing of leaves or other natural structures.
How do the patterns on animals like leopards and zebras form?
-The patterns on animals are related to chemical processes during embryonic development, as explained by Alan Turing's work on morphogenesis. These processes can result in spots, stripes, or uniform colors on the skin of animals.
What is the relationship between Fibonacci numbers and the areas of squares in a golden rectangle?
-The areas of the squares cut from a golden rectangle are in the ratio of successive Fibonacci numbers. This relationship creates a spiral that is reminiscent of those seen in nature, such as in nautilus shells.
What is iridescence and how does it create color in nature?
-Iridescence is a phenomenon where microscopic structures in animals like birds and insects split white sunlight into its component colors, creating vibrant and changing colors not based on pigments but on light interference.
What causes a rainbow and what geometrical conditions are necessary for its formation?
-A rainbow is caused by the scattering and refraction of sunlight by raindrops. Specific conditions are required, such as the sun being at a low angle and rain present, with the observer positioned with their back to the sun.
What is a glory and how does it relate to atmospheric optical phenomena?
-A glory is a circular colored phenomenon seen from the shadow side of an object above clouds, caused by backscattering of light by cloud droplets. It is part of a range of atmospheric optical phenomena influenced by the interaction of sunlight with water droplets or ice crystals.
Why is mathematics described as 'the greatest show on earth' in the context of this script?
-Mathematics is referred to as 'the greatest show on earth' because of its ubiquitous presence and influence in natural phenomena, from the patterns in nature to atmospheric optical effects, demonstrating the beauty and complexity of mathematical principles at work in the world.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
5.0 / 5 (0 votes)