📢 ESPACIOS VECTORIALES de MATRICES💥 Bases y coordenadas. Álgebra Lineal #matematicas
Summary
TLDREl video ofrece una explicación detallada sobre cómo demostrar que un conjunto de matrices forma una base en el espacio vectorial de matrices 2x2. Seguidamente, calcula las coordenadas de una matriz dada con respecto a esta base y finalmente, se determina la expresión matricial de otra matriz utilizando las coordenadas correspondientes. El proceso ilustra cómo trabajar con espacios vectoriales en el contexto de matrices, utilizando un enfoque lógico y sistemático para llegar a las conclusiones.
Takeaways
- 📚 El video trata sobre la demostración de que un conjunto de matrices es una base en el espacio vectorial de matrices 2x2.
- 🔍 Se busca calcular las coordenadas de una matriz dada con respecto a esta base.
- 📉 Para demostrar que un conjunto es una base, es suficiente con probar que es un sistema lineal independiente, dado que el espacio vectorial M2x2 tiene dimensión 4.
- 📈 Se utiliza la combinación lineal de matrices para establecer una ecuación que resulta en un sistema de ecuaciones lineales, la cual se resuelve para demostrar la independencia del sistema.
- 📝 Se resuelve el sistema de ecuaciones obteniendo que los coeficientes alfa, beta, gamma y delta deben ser cero para que la combinación lineal sea nula, lo que prueba la independencia.
- 🎯 Una vez demostrada la independencia, se concluye que el conjunto de matrices es una base, ya que coinciden en el número de vectores con la dimensión del espacio vectorial.
- 📐 Se calculan las coordenadas de la matriz dada 'A' con respecto a la base, resolviendo un nuevo sistema de ecuaciones lineales que surge al comparar elementos de las matrices.
- 🧩 Se describe el proceso de calcular la expresión matricial de una matriz 'M' dada por sus coordenadas con respecto a la base, a través de una combinación lineal de los vectores base.
- 📝 Se resuelve el sistema de ecuaciones para encontrar los valores de alfa, beta, gamma y delta, que son las coordenadas de la matriz 'A' con respecto a la base.
- 🔢 Se presenta la matriz 'M' resultante de la combinación lineal de la base, mostrando cómo se obtienen los nuevos elementos de la matriz a partir de los coeficientes.
- 🎬 El video incluye música de fondo y se enfoca en asegurar que no haya dudas sobre el proceso de demostración y cálculo.
Q & A
¿Qué es un espacio vectorial y cómo se relaciona con las matrices 2x2?
-Un espacio vectorial es una estructura algebraica que permite la adición y escalado de elementos, y en este caso, se refiere a las matrices 2x2, que son matrices con dos filas y dos columnas, y forman un espacio vectorial debido a que cumplen con las propiedades de los espacios vectoriales.
¿Qué es una base en el contexto de espacios vectoriales de matrices?
-Una base en el contexto de espacios vectoriales de matrices es un conjunto de matrices linealmente independientes que generan todo el espacio vectorial. Es decir, cualquier matriz 2x2 se puede expresar como una combinación lineal de las matrices de la base.
¿Cómo se demuestra que un conjunto de matrices es una base de un espacio vectorial?
-Para demostrar que un conjunto de matrices es una base, se debe probar que son linealmente independientes y que el número de matrices en el conjunto es igual a la dimensión del espacio vectorial. En el script, se demuestra que el sistema es linealmente independiente a través de una combinación lineal que resulta en la matriz nula, lo que implica que los coeficientes son cero.
¿Qué es una combinación lineal y cómo se utiliza en la demostración de la base?
-Una combinación lineal es una suma ponderada de vectores, donde los pesos son escalares. Se utiliza para probar la independencia lineal de un conjunto de vectores; si la única combinación lineal que resulta en el vector nulo es la que tiene coeficientes nulos, entonces los vectores son linealmente independientes.
¿Cómo se calculan las coordenadas de una matriz con respecto a una base dada?
-Para calcular las coordenadas de una matriz con respecto a una base dada, se expresa la matriz como una combinación lineal de las matrices de la base. Luego, se resuelve el sistema de ecuaciones que surge de igualar los elementos correspondientes para encontrar los coeficientes de la combinación lineal, que son las coordenadas.
¿Qué significa que una matriz tenga coordenadas (1, -1, 0, -1) con respecto a una base?
-Que la matriz se puede expresar como la suma ponderada de las matrices de la base, donde los pesos son los números 1, -1, 0 y -1 respectivamente, multiplicados por las matrices correspondientes de la base.
¿Cómo se determina si un sistema de matrices es generador del espacio vectorial M2x2?
-Un sistema de matrices es generador del espacio vectorial M2x2 si cualquier matriz 2x2 puede ser expresada como una combinación lineal de ese sistema. En el script, se demuestra que el sistema es generador ya que tiene el mismo número de elementos que la dimensión del espacio vectorial y es linealmente independiente.
¿Cuál es la base canónica de M2x2 y cómo se relaciona con el concepto de base?
-La base canónica de M2x2 es el conjunto de matrices identidad y matrices con un solo elemento distinto de cero en cada posición posible. Es un ejemplo de base porque cualquier matriz 2x2 se puede escribir como combinación lineal de estas matrices.
¿Cómo se obtiene la expresión matricial de una matriz dada a partir de sus coordenadas con respecto a una base?
-Se multiplica cada coordenada por la matriz correspondiente de la base y se suman los resultados. En el script, se muestra cómo realizar esta operación para obtener la expresión matricial de la matriz M dada sus coordenadas.
¿Por qué es importante determinar si un conjunto de matrices es una base o no?
-Es importante porque si un conjunto de matrices es una base, entonces se puede utilizar para representar cualquier otra matriz en el espacio vectorial como una combinación lineal de estas matrices, lo que facilita el análisis y la manipulación de matrices en el espacio vectorial.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

BASE de un ESPACIO VECTORIAL Ejercicios RESUELTOS Álgebra Lineal
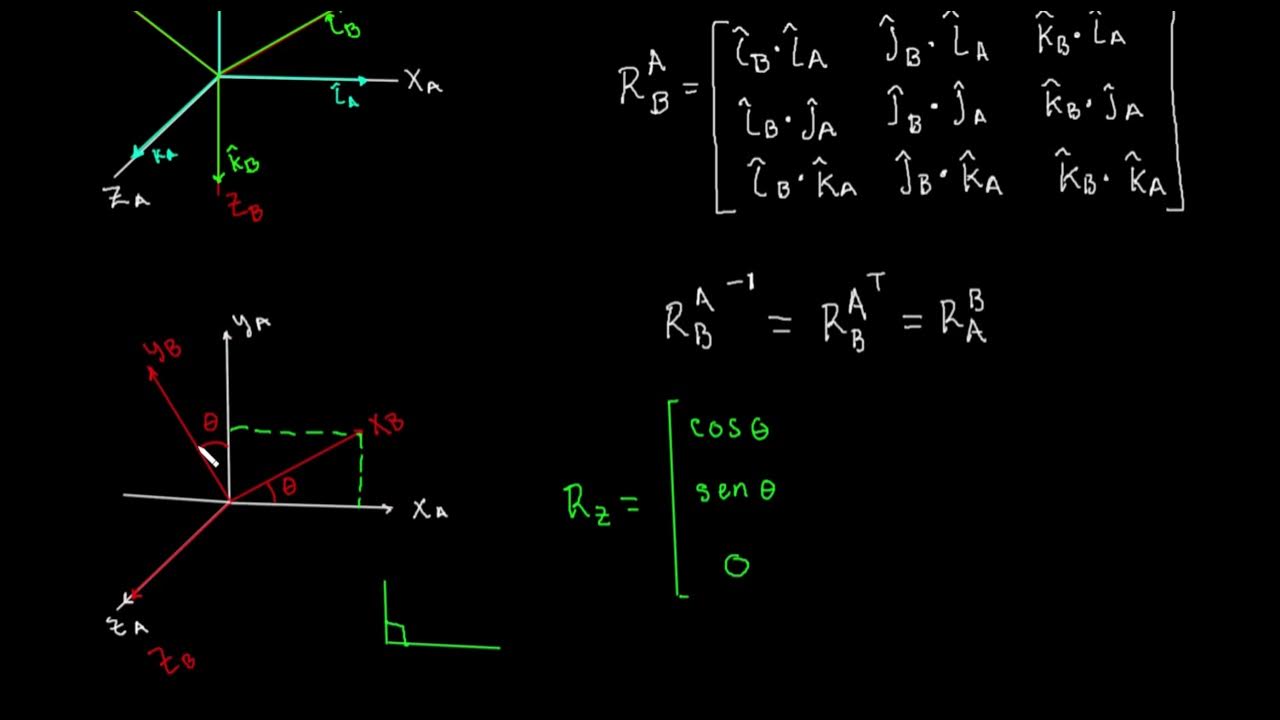
Matrices de rotación en 3D de x, y, z

SUBESPACIOS Vectoriales | 2 Ejercicios RESUELTOS

Multiplicación matricial como composición | Esencia del álgebra lineal, capítulo 4a

Producto vectorial bajo la luz de las transformaciones lineales | Álgebra lineal, capítulo 8b

APLICACIONES DE LAS MATRICES A PROBLEMAS ECONÓMICO-ADMINISTRATIVOS
5.0 / 5 (0 votes)
