Intervalo de confianza para la proporción de la población
Summary
TLDREn este video, se explica cómo calcular el intervalo de confianza para una proporción de la población a partir de una muestra. La fórmula utilizada incluye el margen de error basado en el valor z alfa sobre 2, multiplicado por el error estándar, el cual se calcula como la raíz cuadrada de (p * (1 - p)) / n. Se ilustra con un ejemplo práctico: determinar la proporción de alumnos que aprueban un examen en una escuela, con un nivel de confianza del 95%. El resultado muestra que, con un margen de error del 5%, la proporción poblacional que aprobaría el examen está entre el 69% y el 91%.
Takeaways
- 📚 El video enseña cómo calcular el intervalo de confianza para una proporción de la población.
- 🔢 Se utiliza la fórmula del intervalo de confianza que incluye el valor p (proporción muestral), el margen de error y el valor z alfa sobre 2.
- 📏 El margen de error se define como el valor z alfa sobre 2 multiplicado por el error estándar.
- 📉 El error estándar se calcula como la raíz cuadrada de (p * (1 - p)) dividido por el tamaño de la muestra (n).
- 📈 La proporción es una parte de la población o muestra que cumple con una cierta característica, como el porcentaje de alumnos aprobando un examen.
- 📉 El intervalo de confianza se calcula como p más o menos (z alfa sobre 2 * error estándar).
- 🔢 Para un nivel de confianza del 90%, el valor z alfa sobre 2 es 1.645, y para el 95%, es 1.96.
- 📝 Se presenta un ejemplo práctico donde se calcula el intervalo de confianza para la proporción de alumnos aprobando un examen en una escuela.
- 👨🎓 En el ejemplo, se toma una muestra de 50 estudiantes, de los cuales 40 aprobaron el examen.
- 📊 La proporción p se calcula dividiendo el número de estudiantes aprobados (40) entre el tamaño de la muestra (50), dando como resultado 0.8.
- 📐 El intervalo de confianza resultante para este ejemplo es del 69% al 91%, con un nivel de confianza del 95%.
- 💡 El intervalo de confianza nos da una medida del grado de certeza de que la proporción poblacional está dentro de ese rango.
Q & A
¿Qué es un intervalo de confianza para una proporción de la población?
-Un intervalo de confianza para una proporción de la población es un rango numérico que, con un cierto nivel de confianza, contiene el valor real de la proporción en la población. Es utilizado para hacer inferencias estadísticas a partir de una muestra.
¿Cómo se calcula el margen de error en el intervalo de confianza para una proporción?
-El margen de error se calcula como el valor z alfa sobre 2 multiplicado por el error estándar, donde el error estándar es la raíz cuadrada de (p * (1 - p)) / n, con p como la proporción en la muestra y n como el tamaño de la muestra.
¿Qué es el valor z alfa sobre 2 y cómo se utiliza en la fórmula del intervalo de confianza?
-El valor z alfa sobre 2 es un valor z que se utiliza para determinar el margen de error en un intervalo de confianza. Depende del nivel de confianza seleccionado; por ejemplo, para un 95% de confianza, z alfa sobre 2 es 1.96.
¿Qué es una proporción en el contexto de una muestra estadística?
-Una proporción en el contexto de una muestra estadística es la fracción de la muestra que cumple con una cierta característica o condición, como el porcentaje de alumnos que aprueban un examen.
¿Cómo se calcula la proporción p en la muestra?
-La proporción p se calcula dividiendo el número de individuos en la muestra que cumplen con la característica de interés por el tamaño total de la muestra.
¿Cuál es el nivel de confianza utilizado en el ejemplo del script?
-En el ejemplo del script, se utiliza un nivel de confianza del 95% para calcular el intervalo de confianza.
¿Cuál es el tamaño de la muestra en el ejemplo proporcionado en el script?
-En el ejemplo, el tamaño de la muestra es de 50 estudiantes.
¿Cuántos estudiantes aprobaron el examen en el ejemplo del script?
-En el ejemplo, 40 estudiantes aprobaron el examen.
¿Cómo se calcula el intervalo de confianza para la proporción de alumnos que aprobaron el examen en el ejemplo?
-Se calcula sustituyendo la proporción p (0.8), el valor z alfa sobre 2 (1.96) y el tamaño de la muestra (50) en la fórmula del intervalo de confianza y realizando los cálculos correspondientes.
¿Cuál es el intervalo de confianza calculado para la proporción de alumnos que aprobaron el examen en el ejemplo?
-El intervalo de confianza calculado es del 69% al 91%, lo que significa que con un 95% de confianza, la proporción real de la población que aprobaría el examen se encuentra dentro de este rango.
¿Qué conclusión se puede sacar del intervalo de confianza calculado en el ejemplo?
-La conclusión es que hay un 95% de confianza de que la proporción real de la población que aprobaría el examen está entre el 69% y el 91%.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Intervalo de confianza de la proporción poblacional
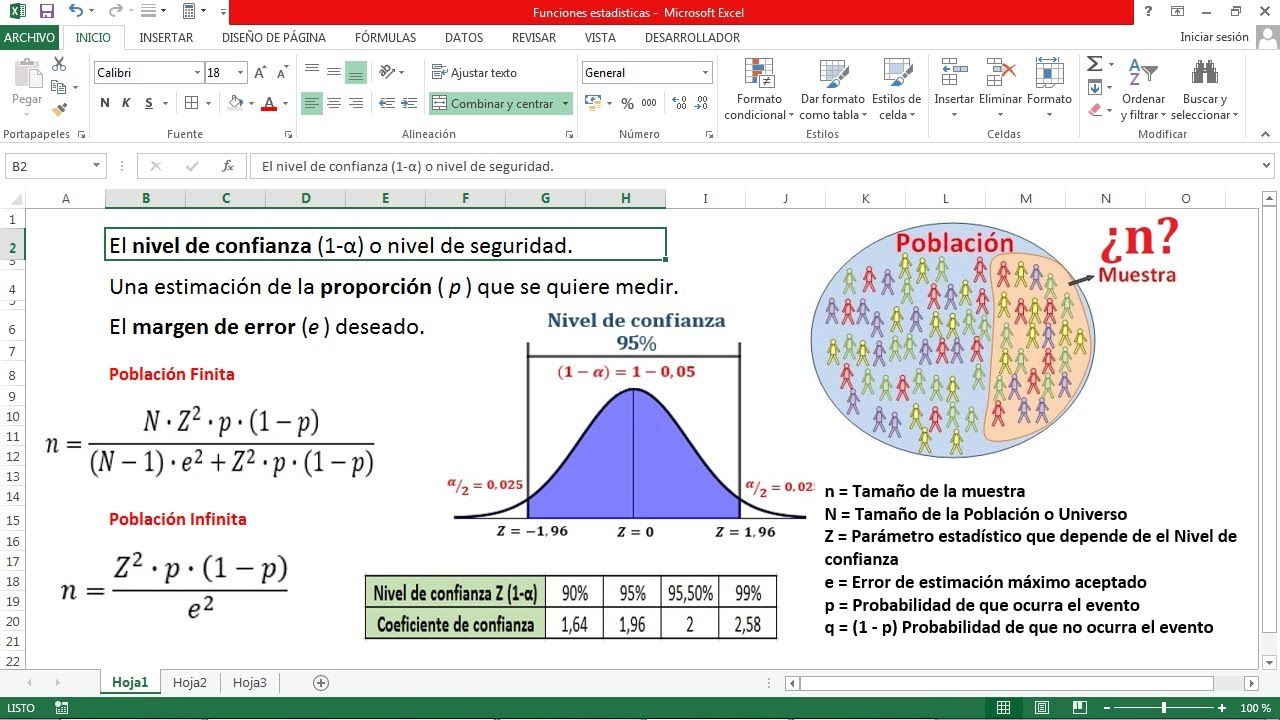
Cómo Calcular el Tamaño de la Muestra para Población Finita y Población Infinita con Excel.

Tamaño de Muestra para Variables Cualitativas con Población Indefinida

Como Calcular el tamaño de la Muestra.wmv

Estimación de parámetros - Parte 1

Estimación de la proporción poblacional
5.0 / 5 (0 votes)
