Part 1: Formal Definition of a Limit
Summary
TLDRThis video introduces the formal definition of limits in calculus. It begins with an informal explanation, showing how a limit exists when the function approaches the same value from both sides of a point. The video then dives into the precise mathematical definition involving epsilon (vertical distance) and delta (horizontal distance) to prove that a limit exists. Through an example, the video demonstrates the process of finding a relationship between epsilon and delta and using it to rigorously prove a limit. The goal is to equip viewers with the understanding to formally prove limits exist.
Takeaways
- 😀 The concept of a limit involves approaching a certain value (C) from both the left and right sides, with the function value approaching a particular point (L).
- 😀 A limit exists if the function approaches the same value from both sides, even if the function is not defined at the point C (e.g., a hole in the graph).
- 😀 The formal definition of a limit involves the relationship between epsilon (vertical distance) and delta (horizontal distance) to prove that a limit exists.
- 😀 Epsilon (ε) represents a vertical distance from the limit L, and delta (δ) represents a horizontal distance from the point C.
- 😀 The goal in proving a limit is to show that for any vertical distance ε, there exists a corresponding horizontal distance δ such that the function value is within the vertical range around L.
- 😀 Graphically, if given ε (a vertical interval), we can find δ (a horizontal interval) such that any x in the interval [C-δ, C+δ] produces f(x) within [L-ε, L+ε].
- 😀 To prove a limit, you start with an inequality involving the absolute values of the difference between f(x) and L, and manipulate this inequality to match the form involving the absolute value of x - C.
- 😀 In the example of the linear function 1/3x + 1, the process involves substituting values, simplifying the absolute value expression, and establishing a relationship between ε and δ.
- 😀 The process of proving the limit involves working backwards from the desired conclusion, finding the relationship between ε and δ, and then moving forward to construct the proof.
- 😀 The final proof demonstrates that if the absolute value of (x - C) is less than δ, then the absolute value of (f(x) - L) is less than ε, confirming the limit exists.
Q & A
What is the informal definition of a limit?
-The limit of a function as x approaches a specific value exists if, as x approaches that value from both the left and right, the function values approach the same value.
How is the limit represented graphically?
-Graphically, the limit is represented by the function values approaching a specific y-value (L) as x approaches a particular x-value (C), even if the function is not defined at x = C.
What does the formal definition of a limit state?
-The formal definition states that for every ε > 0, there exists a δ > 0 such that if the distance between x and C is less than δ, the distance between f(x) and the limit L is less than ε.
What is the role of ε and δ in the formal definition of limits?
-ε (epsilon) represents a vertical distance from the limit L, and δ (delta) represents a horizontal distance from the point C. They are related in that for any given ε, a corresponding δ can be found such that the function's output stays within ε of L when x is within δ of C.
What does the absolute value in the definition of limits represent?
-The absolute value represents distance. In the definition, |x - C| represents the horizontal distance between x and C, and |f(x) - L| represents the vertical distance between f(x) and the limit L.
Why is the function value f(x) not required to be defined at x = C?
-The function does not need to be defined at x = C for the limit to exist. The limit concerns the behavior of the function as x approaches C, not the actual value of the function at C.
What is the first step in proving that a limit exists?
-The first step is to start by expressing the absolute value of f(x) - L as less than ε, and then manipulate the expression to match the form of |x - C|, which is used to establish the relationship between ε and δ.
In the example given, how is the limit of f(x) = 1/3x + 1 as x approaches 6 proven to be 3?
-In the example, the absolute value |f(x) - 3| is manipulated to match the form |x - 6|. By multiplying both sides by 3, the relationship δ = 3ε is established. This allows the proof to proceed from left to right to show that the limit is indeed 3.
How does the relationship between ε and δ allow for the proof of a limit?
-The relationship between ε and δ is key to the proof because it shows that for every vertical distance (ε), a corresponding horizontal distance (δ) exists that keeps the function values within ε of the limit L when x is within δ of C.
What is the significance of the example with the linear function 1/3x + 1?
-The example with the linear function demonstrates the process of proving a limit using the formal definition. It shows how basic algebraic manipulation, such as factoring and multiplying by constants, helps establish the necessary relationship between ε and δ.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus

LIMITE: a Ideia Fundamental do Cálculo
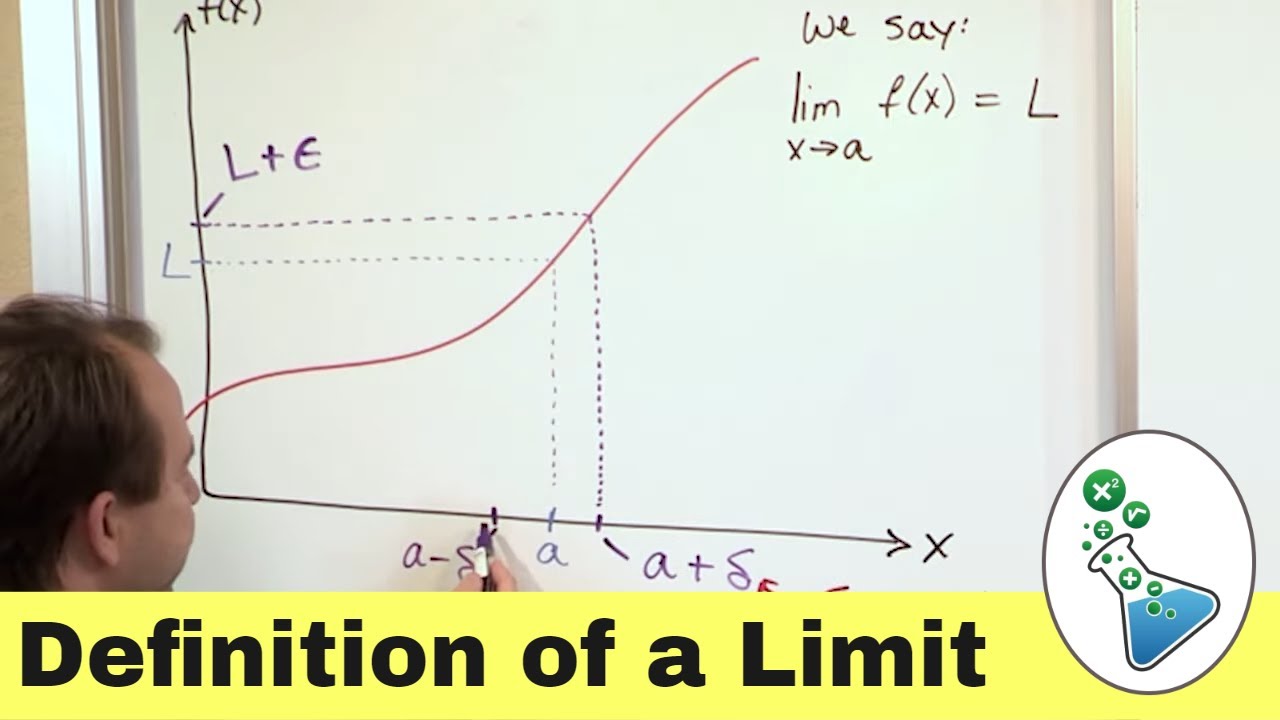
Limits in Calculus: Definition & Meaning. What is a Limit?
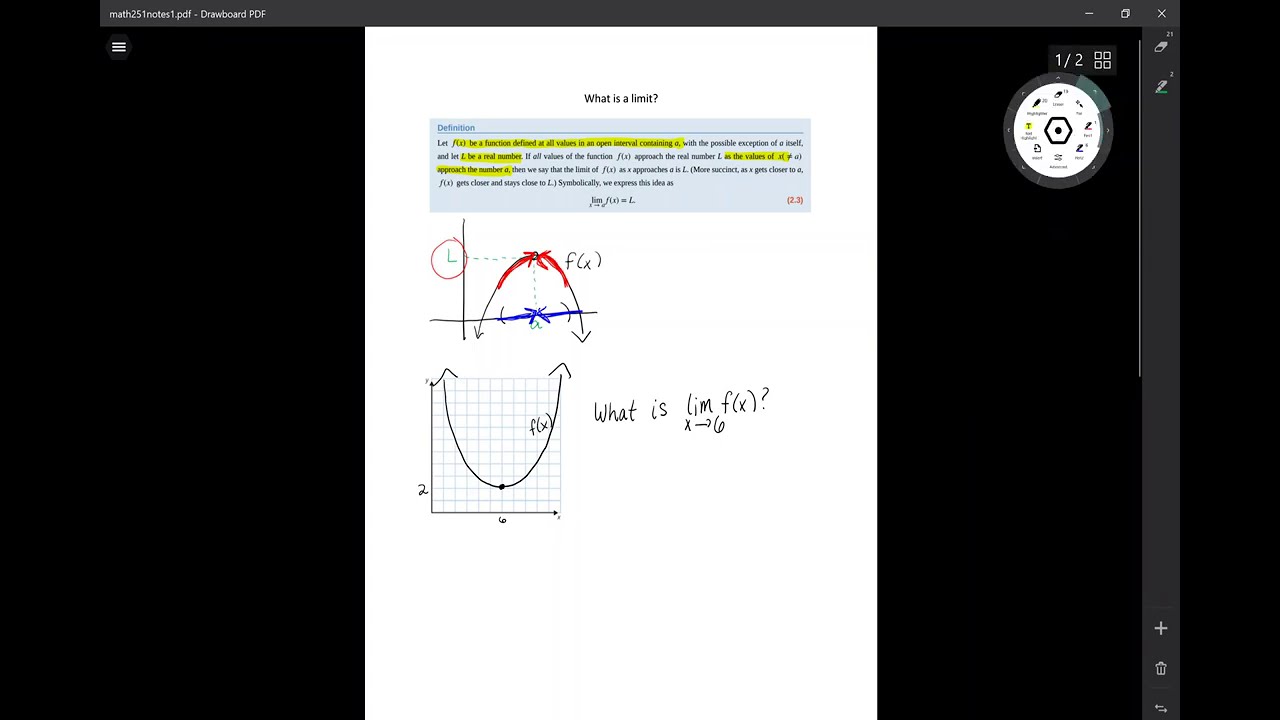
Math 251 - What is a limit?

Limit Kalkulus Part 1: Apa Itu Limit? Penjelasan Mudah & Visual!

Límite de una función real
5.0 / 5 (0 votes)
