PROBSTAT | Bab 6 | Distribusi Khusus - Eksponensial

Summary

This video introduces exponential distribution, particularly in the context of modeling waiting times. The tutorial explains the relationship between exponential and Poisson distributions, highlighting the role of the lambda parameter in defining the distribution's behavior. It covers key concepts like the Probability Density Function (PDF), mean, and variance, and provides a step-by-step example of calculating the probability of a customer being served within a given time. The video emphasizes the importance of understanding these statistical concepts through practical applications and offers helpful tips for learning and solving related problems.

Takeaways

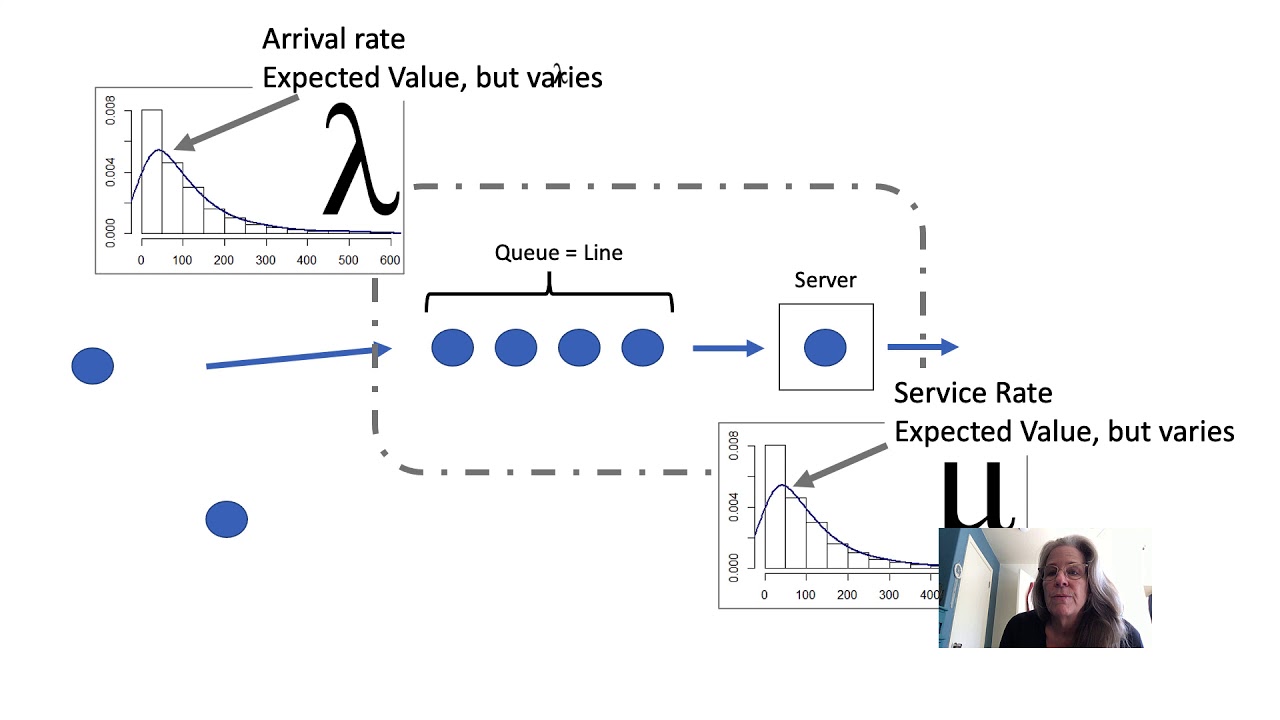
• 😀 Exponential distribution is often used as a model for waiting times or delays.
• 😀 This distribution is closely related to the Poisson distribution, which models discrete random variables.
• 😀 The key parameter of the exponential distribution is lambda (λ), which represents the waiting time rate.
• 😀 Lambda (λ) must be positive and is defined over the interval [0, ∞).
• 😀 The probability density function (PDF) of the exponential distribution is f(x) = λ * e^(-λx) for x ≥ 0 and 0 otherwise.
• 😀 The mean (average) of the exponential distribution is 1/λ, while the variance is 1/λ².
• 😀 A practical example is given with a café, where the average waiting time for a customer is 4 minutes, corresponding to λ = 1/4.
• 😀 To find the probability that a customer is served in less than 3 minutes, the integral of the PDF is used.
• 😀 The integral of the exponential function involves substitution or direct integration methods, leading to a result of approximately 0.527.
• 😀 It is recommended to create a summary table to better understand the distribution type, its notation, PDF/PMF, mean, and variance.
• 😀 The video emphasizes the importance of breaking down complex distributions into manageable parts for better comprehension.

Q & A

What is the exponential distribution commonly used for?

The exponential distribution is commonly used as a model for waiting times or delay times in various processes.

How is the exponential distribution related to the Poisson distribution?

The exponential distribution is closely related to the Poisson distribution, which was discussed in a previous video. The exponential distribution can model the time between events in a Poisson process.

What does the parameter 'lambda' (λ) represent in the exponential distribution?

The parameter 'lambda' (λ) represents the rate of the process, and it indicates the inverse of the average waiting time, meaning it determines how quickly events happen.

What is the domain of the parameter 'lambda'?

The value of 'lambda' must be positive and defined on the interval from 0 to infinity.

What is the probability density function (PDF) of the exponential distribution?

The PDF of the exponential distribution is given by f(x) = λ * e^(-λx) for x >= 0, and 0 for x < 0.

How do you calculate the mean (expected value) of an exponential distribution?

The mean (or expected value) of an exponential distribution is calculated as 1/λ.

What is the variance of an exponential distribution?

The variance of an exponential distribution is 1/λ².

Given a scenario where the average service time in a cafe is 4 minutes, how would you calculate the lambda for the exponential distribution?

Since the mean service time is 4 minutes, and the mean for the exponential distribution is 1/λ, you can calculate λ as 1/4.

How do you calculate the probability of being served in less than 3 minutes?

To calculate the probability of being served in less than 3 minutes, you would integrate the PDF from 0 to 3. This is done by solving the integral of the exponential function with λ = 1/4.

What is the final probability of being served in less than 3 minutes in the given example?

The final probability of being served in less than 3 minutes is approximately 0.527.