13 Karnaugh Map Menyederhanakan Fungsi Boolean - K-Map - Peta Karnaugh
Summary
TLDRThis video tutorial explains the concept of Boolean algebra simplification using Karnaugh Maps (K-Maps). The process involves converting Boolean expressions into Disjunctive Normal Form (DNF) and using K-Maps to group adjacent cells, simplifying the function. The video demonstrates various examples, showing how to group minterms, eliminate redundant terms, and reduce Boolean expressions into simpler forms. The key takeaway is how to efficiently use K-Maps to minimize complex Boolean expressions, making them easier to implement in digital systems. The tutorial also emphasizes the importance of grouping terms correctly and understanding the rules of adjacency and simplification.
Takeaways
- 😀 Boolean functions can be simplified using Karnaugh Maps (K-Maps), which are visual representations of truth tables.
- 😀 A Karnaugh Map (K-Map) consists of a grid where each cell corresponds to a possible combination of variable values, and each cell can be filled with either 0 or 1.
- 😀 To simplify Boolean expressions, input functions must first be in Disjunctive Normal Form (DNF).
- 😀 The process of creating a Karnaugh Map involves labeling the cells based on variable combinations and filling them with the output values from a truth table.
- 😀 A Karnaugh Map can be used to identify adjacent cells with a value of 1, which can then be grouped to simplify the Boolean expression.
- 😀 When grouping 1s in a Karnaugh Map, groups must be in sizes of 2, 4, 8, or 16 to ensure proper simplification.
- 😀 The groups in a Karnaugh Map can only be rectangular or square in shape, and the goal is to create the largest groups possible to simplify the expression.
- 😀 Adjacent cells in a Karnaugh Map can be grouped if they differ by only one variable, either horizontally or vertically.
- 😀 The larger the group of adjacent 1s in a Karnaugh Map, the more variables can be eliminated in the simplified Boolean expression.
- 😀 After grouping the cells, the simplified Boolean expression can be written by considering the common literals across each group.
Q & A
What is the purpose of a Karnaugh map in Boolean algebra?
-A Karnaugh map (or K-map) is used to simplify Boolean functions without the need for algebraic manipulations. It represents the truth table in a visual form, allowing for easy identification of groups of terms to minimize the expression.
What is required for a Boolean function to be used in a Karnaugh map?
-The Boolean function must first be in Disjunctive Normal Form (DNF) before it can be used in a Karnaugh map. This ensures the function consists of a sum of products (minterms).
What does a Karnaugh map look like?
-A Karnaugh map consists of a grid with cells representing all possible combinations of input values. Each cell contains the output value for a corresponding input combination from the truth table, with cells filled with either 1 (true) or 0 (false).
How do you populate a Karnaugh map?
-To populate a Karnaugh map, take the Boolean function in DNF and place 1s in the cells corresponding to the minterms that are true. All other cells are filled with 0.
What is the significance of grouping cells in a Karnaugh map?
-Grouping adjacent cells with 1s in a Karnaugh map helps simplify the Boolean expression by combining terms that differ by only one variable, thus eliminating redundant parts of the expression.
What are the rules for grouping cells in a Karnaugh map?
-Groups of cells must be powers of 2 (e.g., 1, 2, 4, 8, etc.), and the groups must form rectangular or square shapes. Larger groups are preferred as they lead to more simplifications of the Boolean expression.
Can cells in a Karnaugh map be grouped in non-contiguous ways?
-Yes, cells can be grouped across the edges of the map, essentially 'wrapping around' the map. This means that cells on opposite edges of the map can be grouped if they differ by just one variable.
What happens when a Karnaugh map has isolated 1s?
-Isolated 1s should not be left alone. Each isolated 1 must be included in its own group, even if the group size is 1, to ensure it is represented in the simplified Boolean expression.
Why is it important to minimize the number of terms in a Boolean expression?
-Minimizing the number of terms in a Boolean expression reduces complexity, which is beneficial for simplifying logic circuits, reducing cost, and improving performance in digital systems.
What is the final step after grouping cells in a Karnaugh map?
-After grouping the cells, you can write the simplified Boolean expression by identifying the common variables in each group. The variables that remain the same across all the cells in a group form the terms of the simplified expression.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
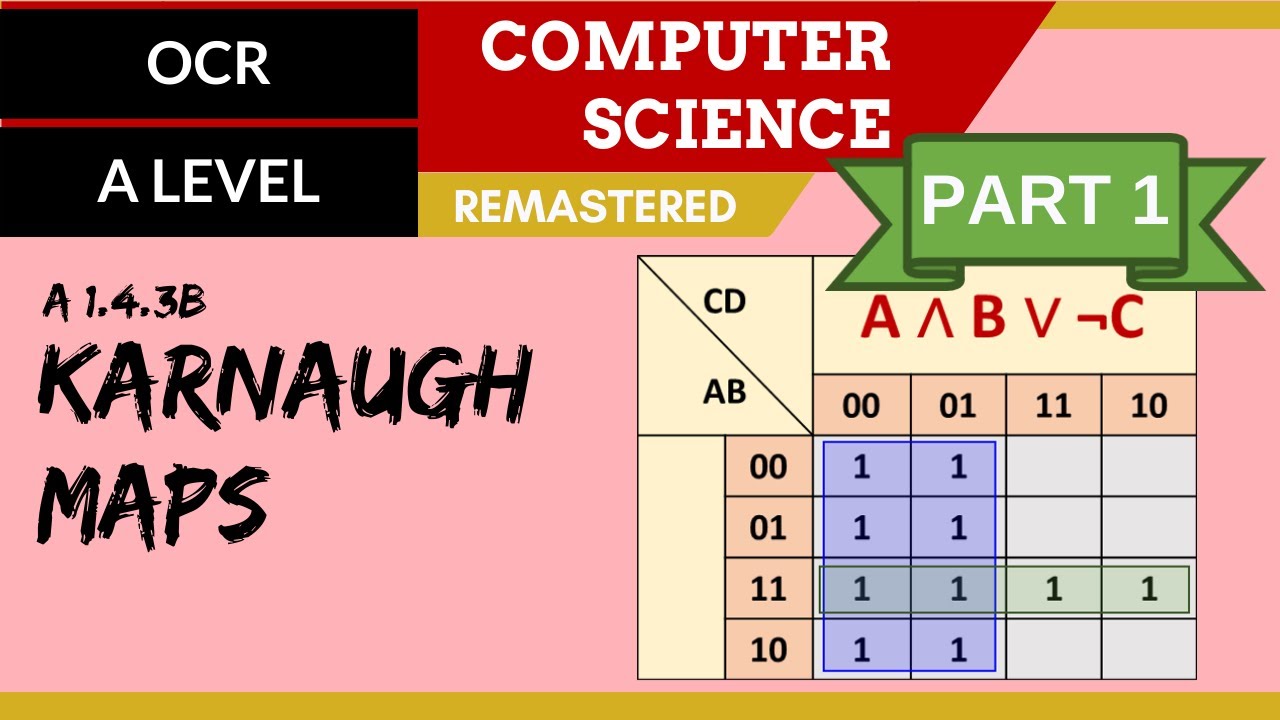
98. OCR A Level (H046-H446) SLR15 - 1.4 Karnaugh maps part 1

101. OCR A Level (H046-H446) SLR15 - 1.4 Karnaugh maps part 4

Quine-McCluskey Minimization Technique (Tabular Method)
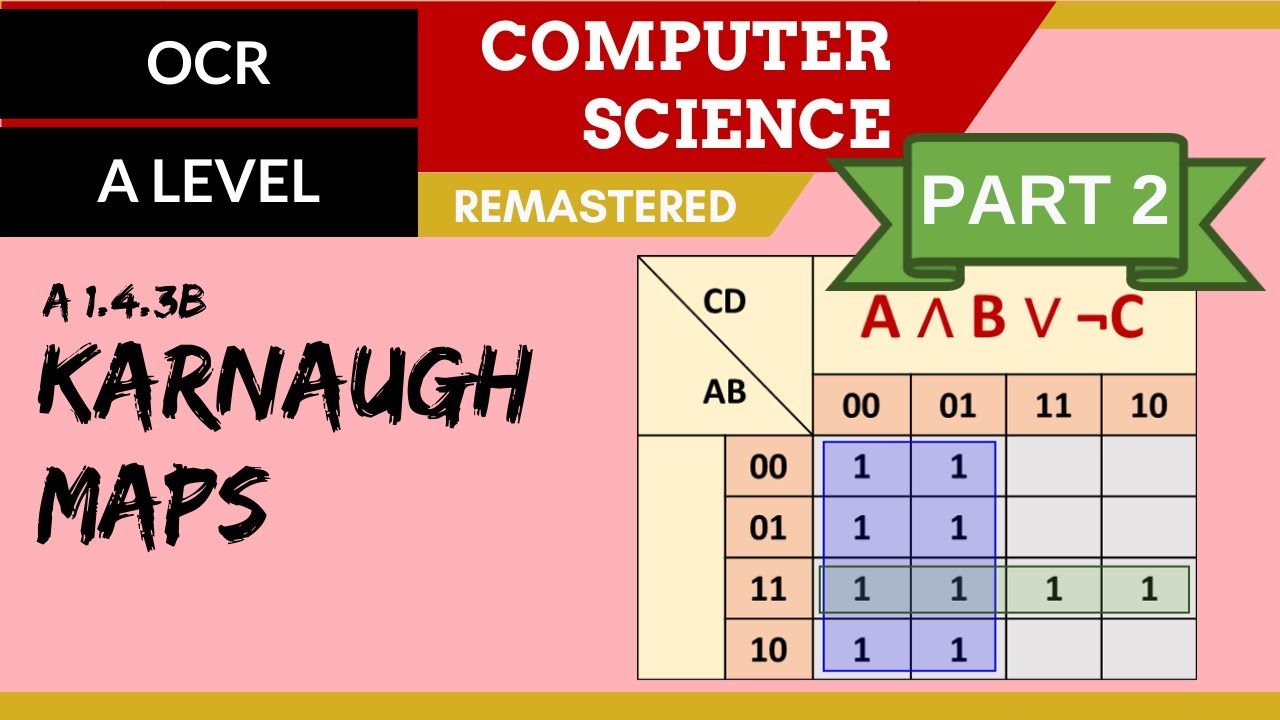
99. OCR A Level (H046-H446) SLR15 - 1.4 Karnaugh maps part 2
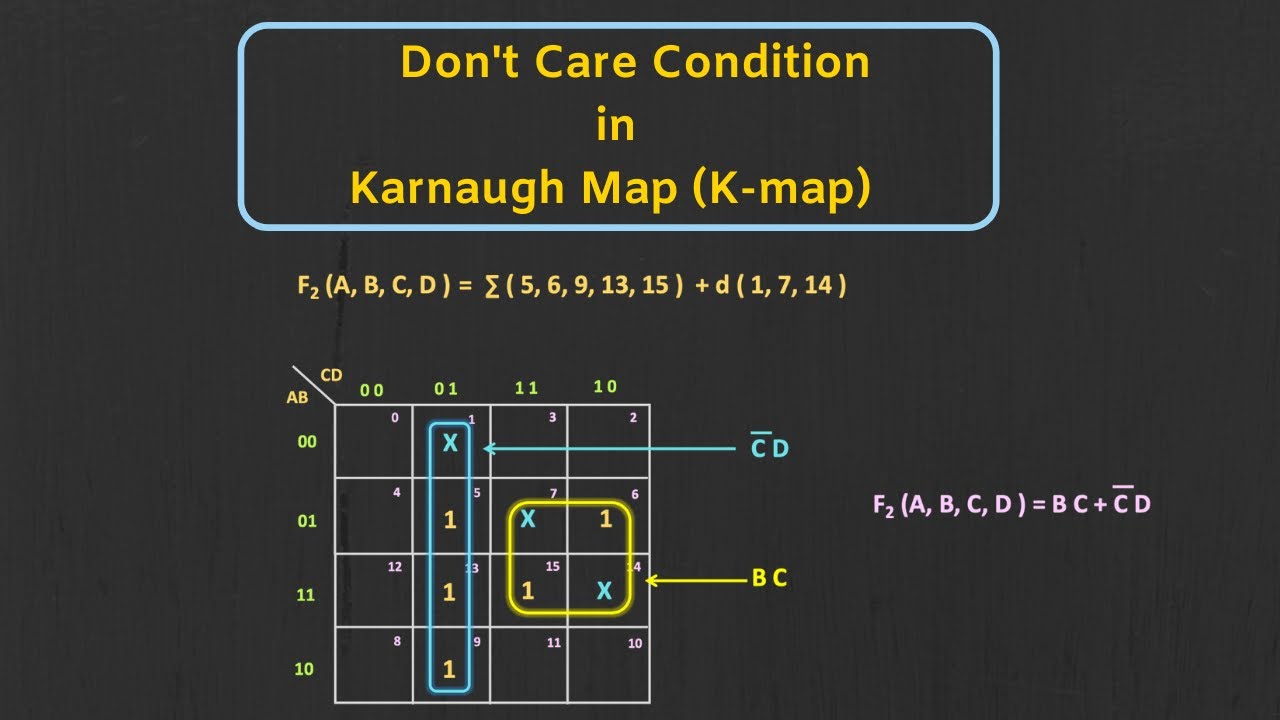
Don't Care Conditions in Karnaugh Map (with Solved Examples)

4 Variable K Map | Minimisation of given Function using K Map | By Mathur Sir
5.0 / 5 (0 votes)
