Understanding the Deflection of Beams
Summary
TLDRThis video delves into the methods engineers use to calculate beam deflections under load, focusing on various approaches such as the double integration method, Macaulay's method, the moment-area method, and Castigliano's theorem. It covers essential concepts like bending moments, curvature, and the impact of different boundary conditions. By explaining these techniques with examples and formulas, the video highlights how these methods enable engineers to predict deflections, ensuring structures remain safe and functional. The sponsor, Brilliant, is also featured as a platform for mastering the necessary calculus skills for tackling such engineering challenges.
Takeaways
- 😀 Beams are crucial in supporting loads in various structures, and engineers must predict their deflection to ensure safety and function.
- 😀 Deflections must remain within allowable limits to avoid damage or failure, even if stresses in the beam are low.
- 😀 Engineers use different methods to predict beam deflection, all assuming elastic deformations and small deflections.
- 😀 The deflection of a beam can be determined by analyzing the elastic curve, where the vertical deflection is related to the distance along the beam.
- 😀 The slope of the beam is defined as the first derivative of the deflection equation, and can be approximated for small deflections.
- 😀 The moment-curvature equation is key to calculating beam deflection, relating bending moment, radius of curvature, and flexural rigidity.
- 😀 The double integration method is a common way to calculate beam deflection, requiring integration of the bending moment equation twice.
- 😀 Boundary conditions, such as displacement and slope at supports, are used to solve the constants of integration when applying the double integration method.
- 😀 Macaulay's method simplifies deflection calculations by using singularity functions to handle varying bending moments along the beam.
- 😀 Superposition allows engineers to combine solutions for different load configurations, making it easier to calculate total deflection.
- 😀 The moment-area method uses the area under the bending moment diagram to calculate deflection and rotation, particularly useful for cantilever beams.
- 😀 Castigliano's theorem provides a powerful energy-based method to calculate deflection, using strain energy and partial derivatives to find the displacement or angle of rotation at a point.
Q & A
Why is it important for engineers to predict beam deflection?
-It is crucial for engineers to predict beam deflection because excessive deflection can cause damage to other parts of the structure, make it unsafe for users, or prevent the beam from fulfilling its intended function, even if stresses are low.
What assumption is made in all the methods discussed for beam deflection?
-All the methods assume that deflections are small and that stresses remain in the elastic region, meaning the deformed shape of the beam is referred to as the elastic curve.
What is the purpose of the moment-curvature equation?
-The moment-curvature equation is used to calculate the curvature of a beam for a given bending moment, helping to understand how the beam will deform under an applied load.
What is the double integration method used for in beam deflection analysis?
-The double integration method is used to calculate the deflection of a beam by integrating the deflection differential equation twice, taking into account the bending moment applied to the beam.
How do boundary conditions help in applying the double integration method?
-Boundary conditions are crucial because they provide information about the beam's deflection and slope at specific points, such as at supports, which helps determine the unknown constants during integration.
What role do Macaulay brackets play in beam deflection analysis?
-Macaulay brackets simplify the deflection calculation process by allowing different terms in the bending moment equation to be activated or deactivated as we move along the beam, making it easier to handle variable loads.
How does the principle of superposition assist in beam deflection analysis?
-The principle of superposition allows engineers to calculate the total deflection by adding the deflections caused by individual loads, making it possible to analyze more complex loading scenarios.
What is the moment-area method, and when is it particularly useful?
-The moment-area method is based on the area under the bending moment diagram. It is especially useful when calculating deflection and rotation at a point along the beam, particularly when the slope at a point is zero, like in cantilever problems.
What is Castigliano's theorem, and how does it relate to beam deflection?
-Castigliano’s theorem relates the deflection at a location of an applied load to the strain energy in the beam. It allows for the calculation of deflections and angles by considering the strain energy and its derivative with respect to the applied load.
What is the significance of mastering calculus for beam deflection analysis?
-Mastering calculus is vital for beam deflection analysis because all the methods discussed—such as the double integration method, moment-area method, and Castigliano's theorem—rely heavily on calculus to derive and solve the equations for deflection and rotation.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Area Moment Method Part 1 - Basic Concepts | Theory of Structures

Plastik Sempurna pada Balok | Cara Menghitung Plastic Section Modulus | Struktur Baja | Lightboard

Metode Pengukuran Debit Saluran Terbuka
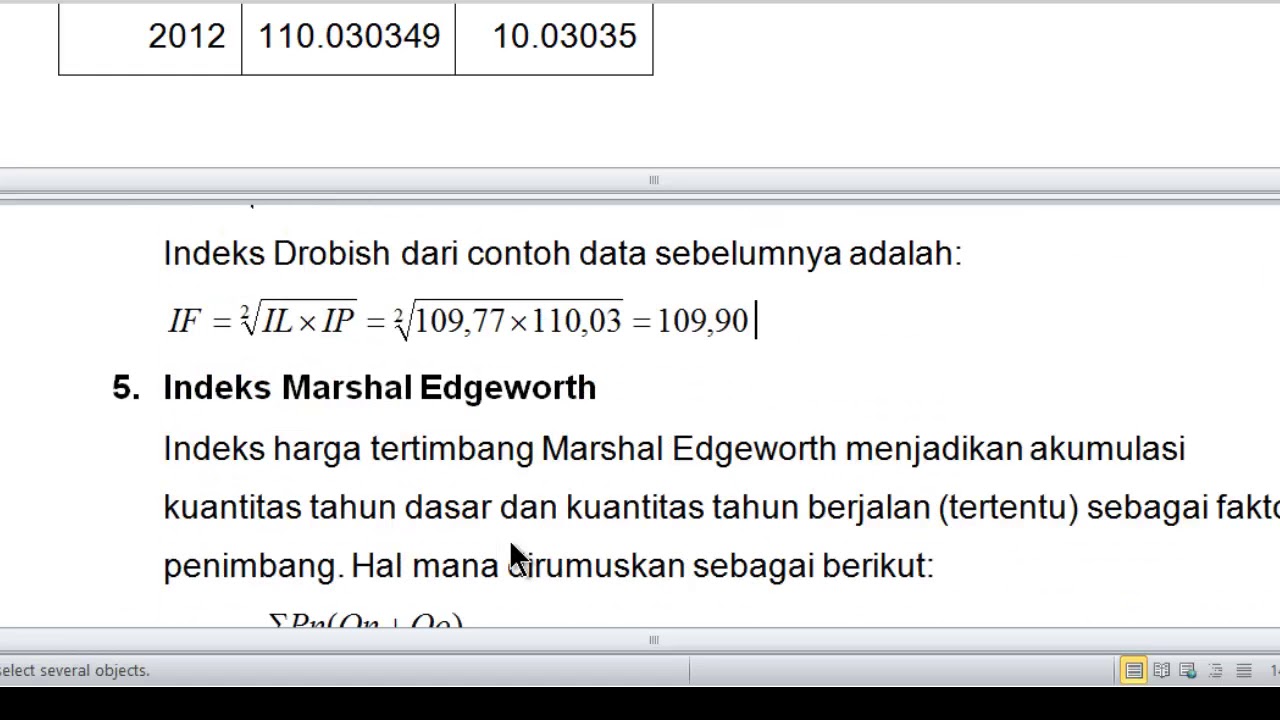
[Statistik1] Pert 12 Angka Indeks Tak Tertimbang

Curso de Integrales. Capítulo 3: La Regla de Barrow. Una propuesta didáctica.
SA21: Virtual Work Method (Trusses)
5.0 / 5 (0 votes)
