Relasi dan Fungsi Matematika Kelas 10 • Part 26: Fungsi Rasional Bentuk 3 - Kuadrat / Linear
Summary
TLDRIn this video, the presenter explains the concept of rational functions, specifically focusing on the third form of rational functions (FX = AX^2 + BX + C / PX + Q). The discussion covers how to determine vertical and oblique asymptotes, find intercepts with the coordinate axes, and analyze the behavior of the graph. The video also includes a step-by-step example to illustrate the process, including finding the graph’s intercepts, asymptotes, and extreme points. The video concludes by noting that certain rational functions may not have extreme points under certain conditions.
Takeaways
- 😀 The video introduces the third form of rational functions, where the function is of the form f(x) = (Ax² + Bx + C) / (Px + Q).
- 😀 The numerator must be a quadratic function, and the denominator must be a linear function for this specific form of rational functions.
- 😀 The video emphasizes that the coefficient of x² in the numerator cannot be zero, as this would change the function type.
- 😀 The denominator's coefficient of x (P) must also not be zero, otherwise the function becomes a constant.
- 😀 The first step in graphing rational functions in this form is finding the vertical and slant asymptotes.
- 😀 Vertical asymptotes occur when the denominator equals zero, and the slant asymptote is determined by dividing the numerator by the denominator.
- 😀 The function in this form can have a slant asymptote, which is not possible for other types of rational functions that only have horizontal asymptotes.
- 😀 To find the x-intercepts, set the numerator equal to zero and solve for x.
- 😀 The y-intercept is found by evaluating the function at x = 0, which involves substituting 0 into the function.
- 😀 The process of finding the function's graph includes determining the regions above and below the x-axis using sign analysis and testing intervals.
- 😀 The video explains how to calculate critical points and points of inflection, and emphasizes that the function may not have any extreme points in some cases.
Q & A
What is the general form of the rational function discussed in the video?
-The rational function discussed in the video is of the form f(x) = (Ax^2 + Bx + C) / (Px + Q), where the numerator is a quadratic function and the denominator is a linear function.
Why must the coefficient of x^2 in the numerator not be zero in this type of rational function?
-The coefficient of x^2 in the numerator must not be zero because if it is zero, the function would no longer be a rational function with a quadratic numerator, but instead a linear function.
What is the condition for the denominator of the rational function?
-The denominator must be a linear function of the form Px + Q, where P cannot be zero, as a zero value for P would result in a constant function instead of a rational function.
What are the main stages in graphing the rational function discussed in the video?
-The stages include: 1) Finding the vertical and slant asymptotes, 2) Determining the points of intersection with the x and y axes, 3) Identifying the domain and range, 4) Finding any extreme points, and 5) Identifying any other points if necessary.
How is the slant asymptote of the function determined?
-The slant asymptote is determined by performing polynomial long division on the numerator and denominator. The result of the division gives the equation of the slant asymptote.
What is the method for finding the x-intercepts of the function?
-The x-intercepts are found by setting the function equal to zero (f(x) = 0) and solving the resulting quadratic equation for x.
How do you find the y-intercept of the rational function?
-The y-intercept is found by setting x = 0 and substituting it into the function. The result gives the y-coordinate of the point where the graph intersects the y-axis.
What does the term 'asymptote' refer to in the context of this function?
-An asymptote is a line that the graph of the function approaches but never touches. There can be vertical, horizontal, or slant asymptotes depending on the function's behavior.
Why does the function not have a horizontal asymptote when it has a slant asymptote?
-A function cannot have both a slant and a horizontal asymptote. If there is a slant asymptote, the function's degree of the numerator is greater than the degree of the denominator, so a horizontal asymptote does not exist.
What is the significance of the factorization step in finding the x-intercepts?
-The factorization of the quadratic expression in the numerator allows for easy identification of the values of x that make the function equal to zero, giving the x-intercepts.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Relasi dan Fungsi Matematika Kelas 10 • Part 27: Soal Fungsi Rasional Bentuk 3 - Kuadrat / Linear
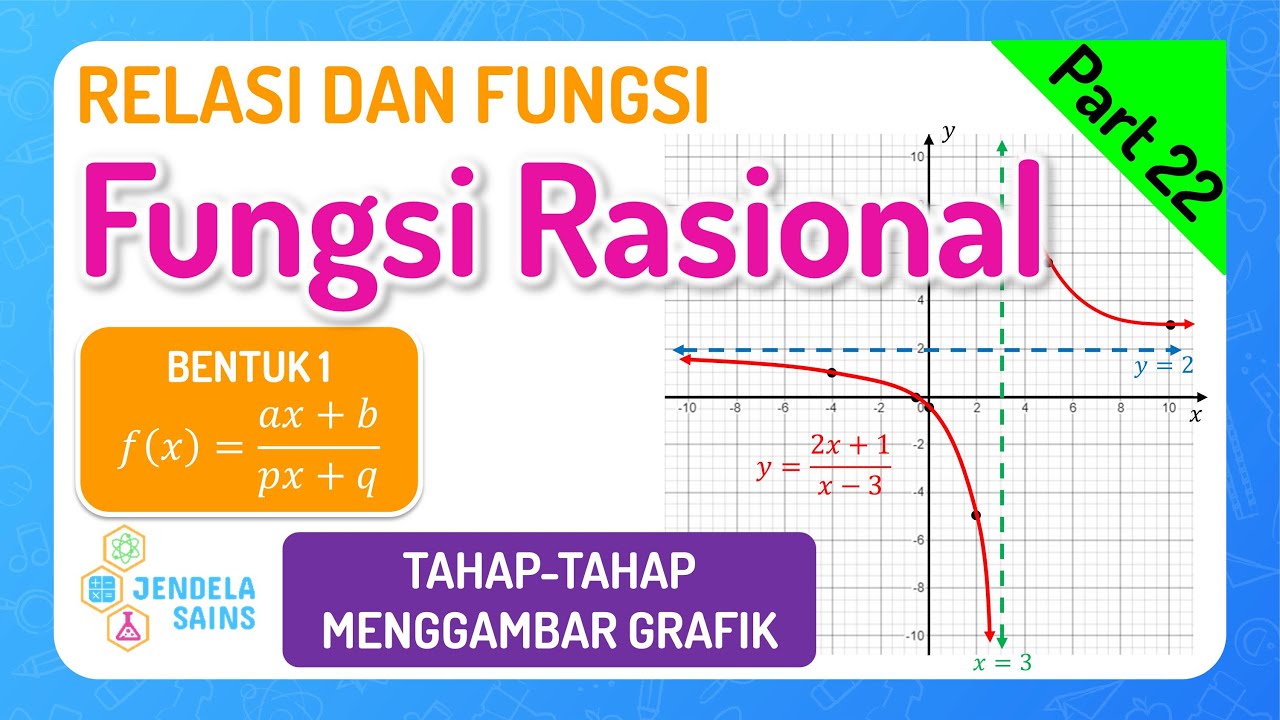
Relasi dan Fungsi Matematika Kelas 10 • Part 22: Fungsi Rasional Bentuk 1 - Linear / Linear
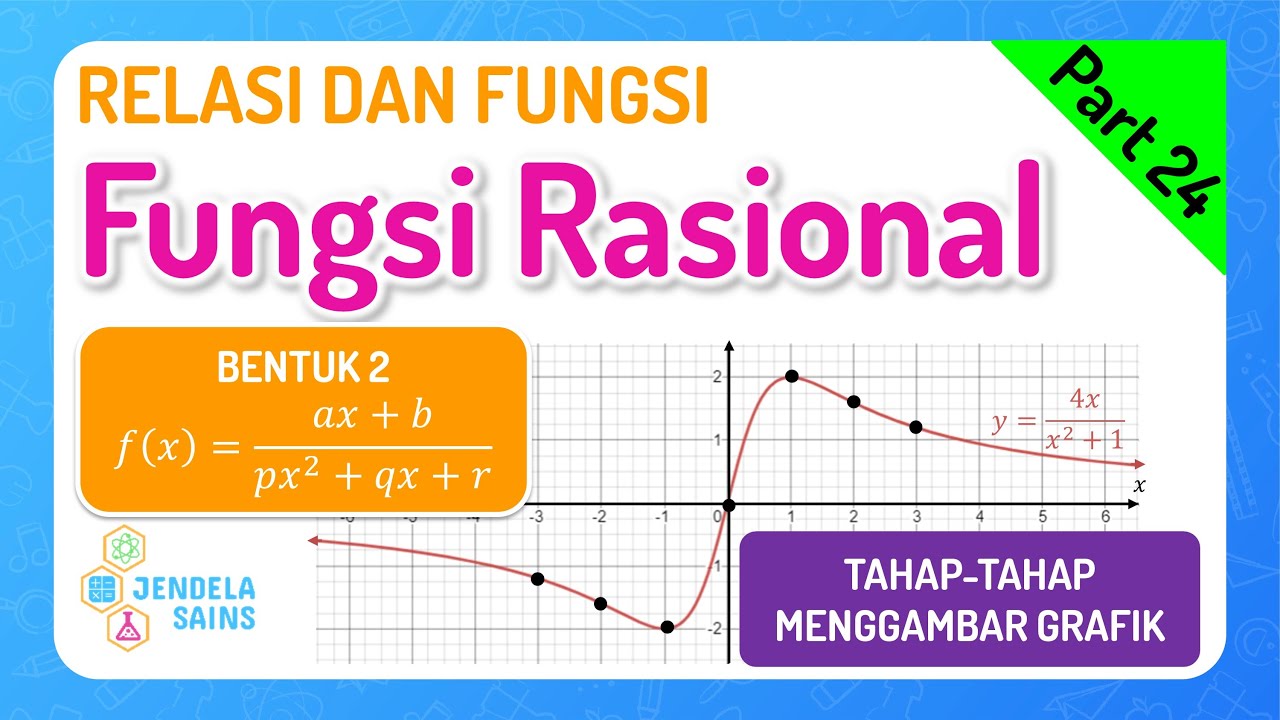
Relasi dan Fungsi Matematika Kelas 10 • Part 24: Fungsi Rasional Bentuk 2 - Linear / Kuadrat

FUNÇÃO DO 2º GRAU: DEFINIÇÃO E GRÁFICO

Rational Functions | General Mathematics

Rumus Fungsi Invers - Matematika SMA Kelas XI Kurikulum Merdeka
5.0 / 5 (0 votes)
