Materi Lingkaran, Unsur Lingkaran dan Hubungan Sudut Pusat Sudut Keliling Kelas XI Kur Merdeka

Summary

In this educational video on circles for 11th-grade students, the lesson explores the definition and key elements of a circle, including its center, radius, diameter, arc, chord, segment, sector, and central angles. It explains how these components relate to each other, with a particular focus on the relationship between central angles and inscribed angles. By using relatable examples like a Ferris wheel and everyday objects, the script emphasizes the importance of understanding circle geometry and the interdependence of these elements. The video concludes with practical examples and exercises to help students apply their knowledge.

Takeaways

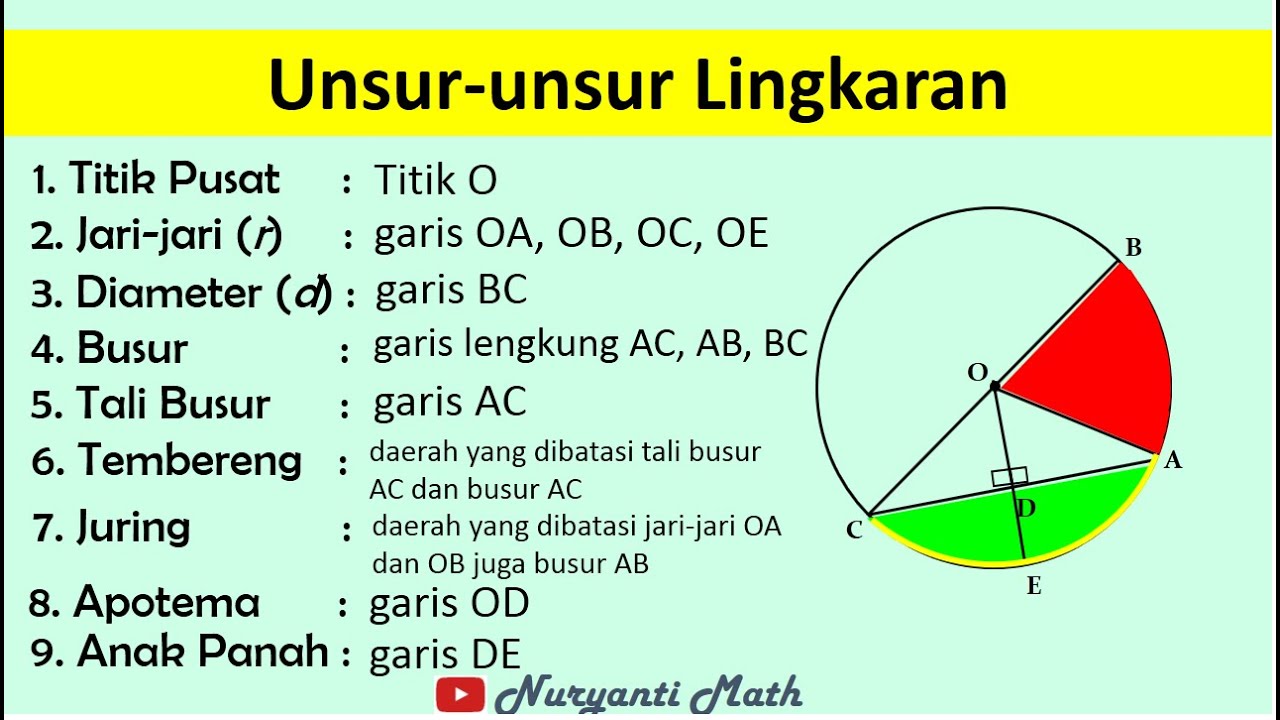
• 😀 Circles are defined as a collection of points equidistant from a central point, called the center of the circle.
• 😀 The essential elements of a circle include the center, radius, diameter, arc, chord, segment, sector, and apothem.
• 😀 The radius is the straight line from the center of the circle to any point on the circumference.
• 😀 The diameter is a line segment passing through the center, connecting two points on the circumference, and is twice the length of the radius.
• 😀 An arc is a curved line between two points on the circumference of the circle.
• 😀 A chord is a straight line that joins two points on the circle's circumference.
• 😀 A sector is the area enclosed by two radii and an arc, while a segment is the area between a chord and an arc.
• 😀 The central angle of a circle is formed by two radii, and its vertex is at the center of the circle.
• 😀 The inscribed (or peripheral) angle is formed by two chords meeting at a point on the circumference, and it subtends an arc.
• 😀 The central angle is always twice the size of the inscribed angle that subtends the same arc, meaning the central angle is twice the measure of the corresponding inscribed angle.

Q & A

What is a circle defined as in geometry?

A circle is defined as the set of all points in a plane that are equidistant from a fixed point, called the center. The distance from the center to any point on the circle is called the radius.

What is the significance of the center of a circle?

The center of a circle is the fixed point that is equidistant from every point on the circumference. It is the point of reference for drawing the circle and defining other components like the radius and diameter.

How do we define the radius of a circle?

The radius of a circle is the straight-line distance from the center of the circle to any point on the circumference. It is denoted by 'R'.

What is the relationship between the radius and the diameter of a circle?

The diameter of a circle is twice the length of the radius. It is the straight line passing through the center and touching the circumference at two points.

What is a chord in a circle?

A chord is a line segment that connects two points on the circumference of the circle. The diameter is a special type of chord that passes through the center.

What is the difference between a central angle and an inscribed angle (circumferential angle)?

A central angle has its vertex at the center of the circle, and its sides are radii of the circle. An inscribed angle (or circumferential angle) has its vertex on the circumference, and its sides are chords of the circle.

What is the formula for the relationship between central angles and inscribed angles?

The central angle is always twice the measure of the inscribed angle that subtends the same arc. In other words, if the central angle is θ, the inscribed angle will be θ/2.

What is a segment in a circle?

A segment is the region bounded by a chord and the arc of the circle. It is often divided into smaller segments, such as a minor or major segment, based on the length of the arc.

How do you calculate the area of a sector in a circle?

The area of a sector can be calculated using the formula: Area = (θ/360) * π * r², where θ is the central angle in degrees and r is the radius of the circle.

What is the rule regarding angles at the circle’s center and angles at the circumference that subtend the same arc?

The angle at the center of the circle is twice the angle at the circumference that subtends the same arc. This is a key geometric property of circles.