Hooke's Law and Elastic Potential Energy

Summary

In this video, we explore Hooke's Law and its application to springs. Hooke's Law describes how the force required to stretch or compress a spring is proportional to the displacement, with the spring constant (k) determining the stiffness. The video covers practical problems, including calculating spring constants, forces, and work required to stretch springs by specific distances. It also delves into concepts like restoring force, elastic potential energy, and how to calculate the work done during spring extension. The tutorial provides a clear explanation of the relationship between force, displacement, and spring constant, with step-by-step examples.

Takeaways

• 😀 Hooke's Law describes the relationship between the force applied to a spring and its displacement. The force is proportional to the displacement: F = kx.
• 😀 The spring constant (k) represents the stiffness of the spring. A higher spring constant means a stiffer spring that requires more force to stretch or compress.
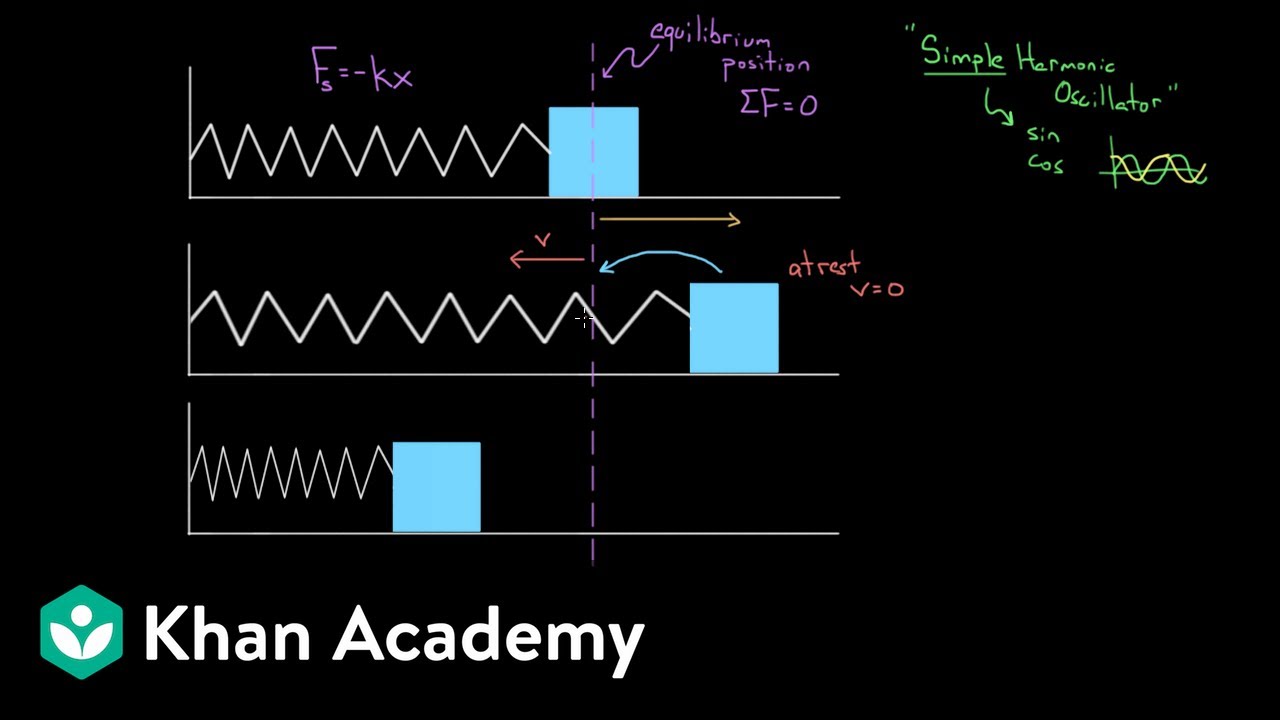
• 😀 The restoring force exerted by a spring is equal in magnitude but opposite in direction to the applied force. It follows the equation F_s = -kx.
• 😀 Hooke's Law applies within the elastic region of the spring. If the spring is stretched or compressed beyond this region, it may not return to its original shape.
• 😀 The work required to stretch a spring is calculated using the formula W = 1/2 k x^2, where x is the displacement from the natural length of the spring.
• 😀 Elastic potential energy stored in a spring is given by the formula U = 1/2 k x^2, where x is the displacement from the spring's natural length.
• 😀 The spring constant k can be calculated as the ratio of the force applied to the displacement, i.e., k = F/x.
• 😀 When calculating work done on a spring, it's important to remember that work is equal to the area under the force vs. displacement graph, which is a triangle for a spring with variable force.
• 😀 The force required to stretch or compress a spring increases linearly with displacement within the elastic region, as shown by the straight line in a force vs. displacement graph.
• 😀 The work done by a spring's restoring force is negative, as the force opposes the direction of displacement, while the work required to stretch the spring is positive.

Q & A

What is Hooke's Law and how does it relate to springs?

Hooke's Law states that the force required to stretch or compress a spring is proportional to the displacement from its natural length. The law is mathematically expressed as F = kx, where F is the force applied to the spring, k is the spring constant, and x is the displacement from the spring's natural length. This relationship holds as long as the spring remains within its elastic region.

What is the spring constant (k), and how does it affect the stiffness of the spring?

The spring constant (k) is a proportionality constant that describes how stiff a spring is. A higher spring constant indicates a stiffer spring that requires more force to stretch or compress by a given distance. For example, a spring with a constant of 300 N/m requires 300 newtons of force to stretch it by one meter, while a spring with a constant of 50 N/m is much easier to stretch.

What happens when you exceed the elastic limit of a spring?

When the elastic limit of a spring is exceeded, the spring no longer follows Hooke's Law. The relationship between the force applied and the displacement breaks down, and the spring may undergo permanent deformation or elongation. Beyond this point, the spring cannot return to its original length after the force is removed.

How is the restoring force related to the applied force in Hooke's Law?

The restoring force (Fs) is equal in magnitude but opposite in direction to the applied force (Fp). When you stretch the spring, the applied force moves the spring in one direction, while the restoring force works to pull the spring back to its natural length, trying to return it to equilibrium. Mathematically, the restoring force is expressed as Fs = -kx.

What units are used for the spring constant, and how do they relate to force and displacement?

The spring constant (k) is measured in newtons per meter (N/m). It describes how much force is needed to stretch the spring by a certain distance. For instance, a spring constant of 50 N/m means that 50 newtons of force are required to stretch the spring by one meter.

How do you calculate the spring constant (k) from force and displacement?

The spring constant (k) can be calculated using Hooke's Law equation: k = F/x, where F is the force applied to the spring and x is the displacement from the spring's natural length. For example, if a 200 N force stretches a spring by 4 meters, the spring constant is k = 200 N / 4 m = 50 N/m.

How do you calculate the force required to stretch a spring by a given displacement?

The force required to stretch a spring can be calculated using Hooke's Law equation: Fp = kx, where k is the spring constant and x is the displacement. For instance, to stretch a spring with a constant of 300 N/m by 45 centimeters (0.45 meters), the required force is Fp = 300 N/m × 0.45 m = 135 N.

What is the work done to stretch a spring, and how is it calculated?

The work done to stretch a spring is the energy required to move the spring from its natural length to a new position. It is calculated by the formula W = 1/2 k (Δx)^2, where k is the spring constant and Δx is the change in displacement. This work represents the elastic potential energy stored in the spring.

What is the difference between work and potential energy in the context of a spring?

Work refers to the energy required to move a spring from one position to another, while potential energy refers to the energy stored in the spring due to its displacement. In a spring, the work done to stretch or compress the spring becomes the elastic potential energy, which is given by the equation PE = 1/2 kx^2.

How can you verify the work done by a spring using energy calculations?

You can verify the work done by a spring by calculating the change in its potential energy. The potential energy at two positions can be computed using PE = 1/2 kx^2. The work done is the difference in the potential energy at the final and initial positions. For example, if the spring's displacement changes from 0.045 m to 0.082 m, you calculate the potential energy at both positions and subtract the initial energy from the final energy to find the work done.