Árbol binario, borrar nodo - 27 - Estructuras de Datos en C#

Summary

La lección se enfoca en el proceso de eliminación de nodos en un árbol binario de búsqueda, abordando cómo encontrar al padre de un nodo y los tres casos posibles para borrar nodos. Se presenta un código para encontrar al padre de un nodo dado y se discuten los casos en los que el nodo a borrar no tiene hijos, tiene un único hijo y tiene dos hijos. Para el caso de nodos con dos hijos, se sugiere encontrar el nodo más pequeño en el subárbol derecho y reemplazar el valor a eliminar con el del nodo más pequeño antes de eliminarlo. Se proporciona un pseudocódigo para guiar en la implementación del proceso de eliminación de nodos, destacando la importancia de mantener la propiedad del árbol binario de búsqueda.

Takeaways

• 📚 En esta lección, se enfoca en el proceso de eliminar un nodo en un árbol binario de búsqueda, incluyendo cómo encontrar al padre de un nodo.
• 🔍 Se presentan tres casos principales para borrar nodos en un árbol binario de búsqueda: el nodo sin hijos, el nodo con un hijo y el nodo con dos hijos.
• 👀 El primer caso, el nodo sin hijos, es el más sencillo de manejar, ya que simplemente se debe desconectar el nodo del árbol.
• 🔗 Para borrar un nodo con un hijo, se debe conectar el padre del nodo a eliminar con su hijo, eliminando así el nodo de la estructura del árbol.
• 📌 En el caso de un nodo con dos hijos, es necesario encontrar el nodo más pequeño en el subárbol derecho y copiar su valor al nodo a eliminar, luego eliminar el nodo con el valor copiado.
• 👶 El proceso para encontrar el padre de un nodo se realiza mediante un método recursivo, que verifica si el nodo actual es el padre del nodo buscado.
• 📈 Se proporciona un pseudocódigo para ilustrar el proceso de eliminación de nodos, el cual debe ser adaptado al código específico del usuario.
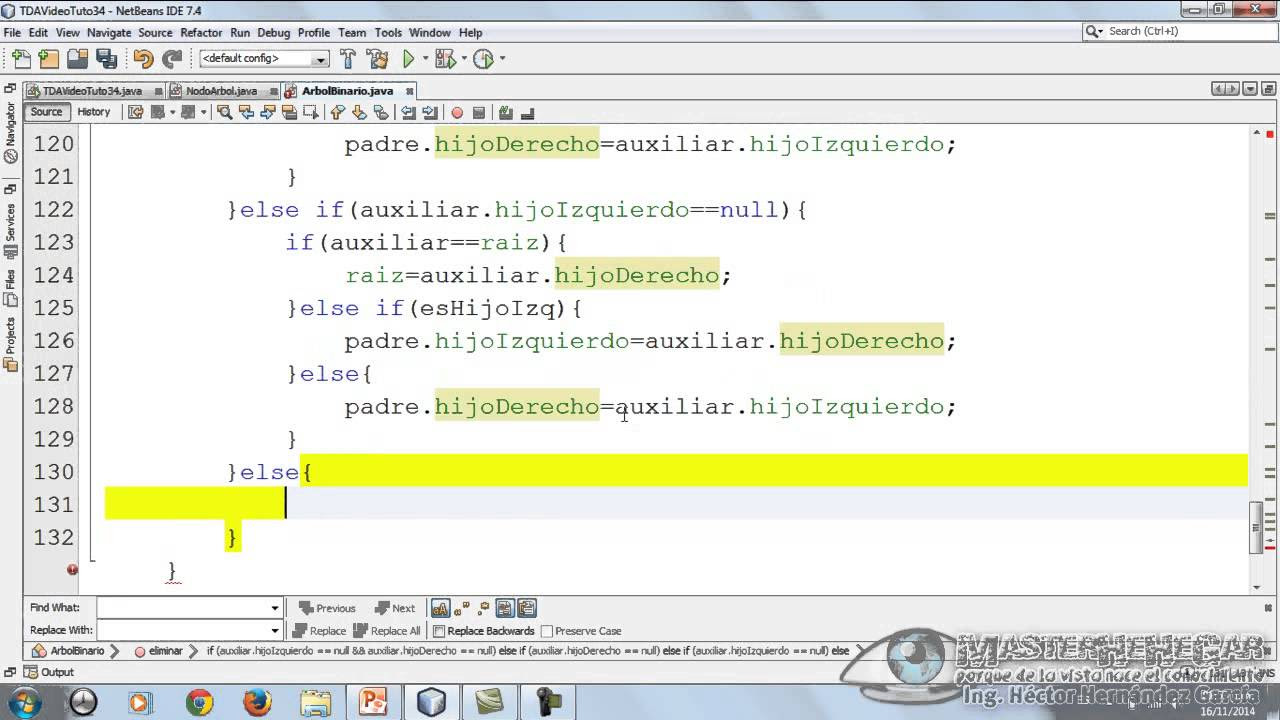
• 🛠️ El pseudocódigo incluye condiciones para manejar los casos de nodos sin hijos, con un hijo y con dos hijos, asegurando que la propiedad del árbol binario de búsqueda se mantenga.
• 🔁 La eliminación de un nodo se realiza de manera recursiva, y es importante tener en cuenta la gestión adecuada de los casos base y la conexión correcta de los nodos restantes.
• ⚙️ Al borrar un nodo con un hijo, se debe tener en cuenta el caso espejo, donde el hijo puede estar en el lado derecho en lugar del izquierdo.
• 🌳 La conservación de la propiedad del árbol binario de búsqueda es crucial para que los nodos menores estén a la izquierda y los nodos mayores a la derecha después de una eliminación.
• ✅ La lección finaliza con una invitación a los estudiantes a dejar sus dudas en los comentarios y se despiden con la promesa de una próxima lección.

Q & A

¿Qué es un árbol binario de búsqueda y cómo se relaciona con la lección?

Un árbol binario de búsqueda es una estructura de datos en la que cada nodo tiene hasta dos hijos y los datos en cada nodo cumplen con la propiedad de ordenamiento: los datos de los nodos a la izquierda son menores al nodo actual y los de la derecha son mayores. La lección se enfoca en cómo borrar nodos de este tipo de árbol.

¿Cuáles son los tres casos para borrar nodos en un árbol binario de búsqueda?

Los tres casos son: 1) Cuando el nodo a borrar no tiene hijos, 2) Cuando el nodo tiene un solo hijo, y 3) Cuando el nodo tiene dos hijos. Cada caso requiere de un enfoque diferente para mantener la propiedad de ordenamiento del árbol.

¿Cómo se puede encontrar el padre de un nodo en un árbol binario de búsqueda?

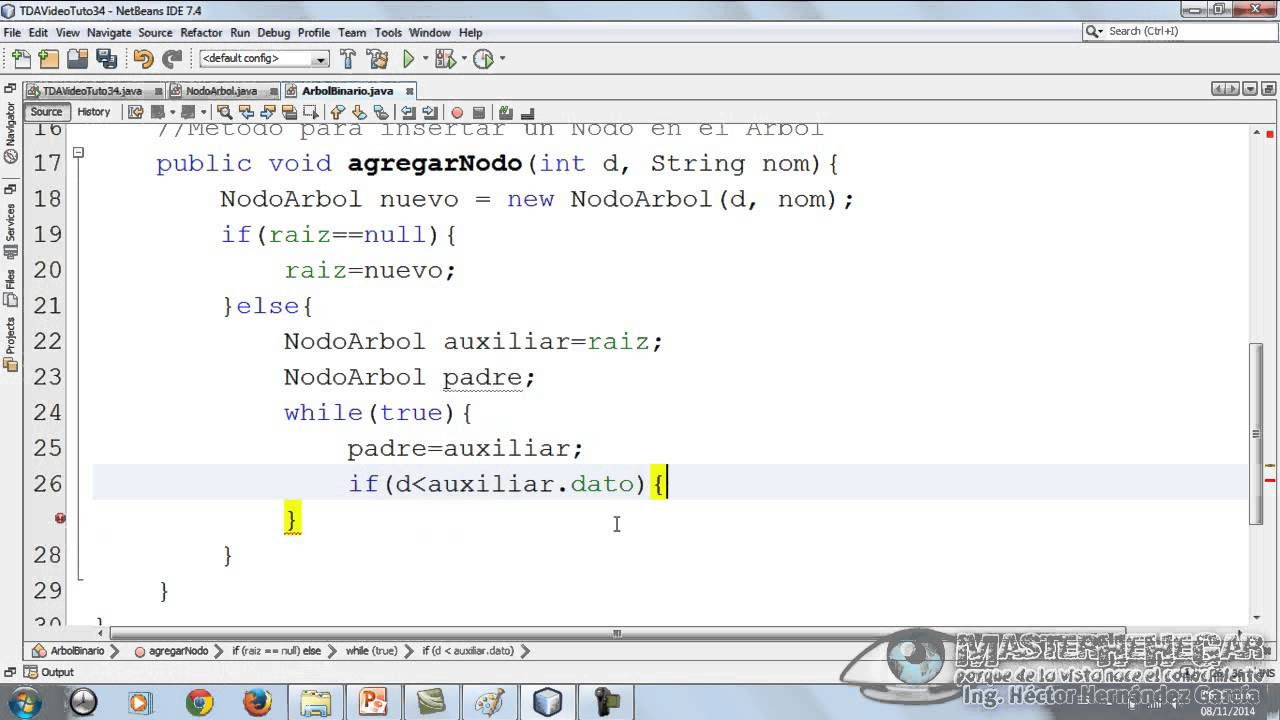
Se puede encontrar el padre de un nodo utilizando un método de búsqueda recursiva que verifica si el dato del hijo es menor o mayor al del nodo actual, lo que indica si el padre se encuentra en el subárbol izquierdo o derecho respectivamente.

¿Qué sucede si se desea borrar un nodo que no tiene hijos?

Si se desea borrar un nodo sin hijos (hoja), se debe establecer la referencia del padre al hijo como null, desconectando así el nodo de la estructura del árbol.

¿Cómo se conecta el padre de un nodo con su hijo si el nodo a borrar tiene un solo hijo?

Si el nodo a borrar tiene un solo hijo, se debe conectar el padre del nodo a borrar con su hijo. Si el hijo es del lado izquierdo, se establece la referencia izquierda del padre en null, y si es del lado derecho, se establece la referencia derecha en null.

¿Qué es el caso más complicado al borrar nodos en un árbol binario de búsqueda?

El caso más complicado es cuando el nodo a borrar tiene dos hijos. Para resolver esto, se debe encontrar el nodo con el valor mínimo en el subárbol derecho del nodo a borrar y luego reemplazar el valor del nodo a borrar por el del nodo encontrado, finalmente se elimina el nodo con el valor mínimo.

¿Cómo se conserva la propiedad del árbol binario de búsqueda después de borrar un nodo con dos hijos?

Se conserva la propiedad del árbol binario de búsqueda al reemplazar el valor del nodo a borrar con el del nodo de valor mínimo en su subárbol derecho (que siempre será un nodo hoja) y luego eliminar ese nodo, lo que no rompe la estructura de búsqueda del árbol.

¿Por qué es importante el orden en el que se realizan las operaciones al borrar un nodo con dos hijos?

Es importante porque al reemplazar el valor del nodo a borrar con el del nodo de valor mínimo del subárbol derecho y luego eliminar ese nodo, se mantiene la estructura de búsqueda del árbol, asegurando que los nodos con valores menores permanecen a la izquierda y los nodos con valores mayores a la derecha.

¿Qué es el pseudocódigo y cómo ayuda en la implementación de la eliminación de nodos en un árbol binario de búsqueda?

El pseudocódigo es una representación de algoritmos que utiliza una sintaxis más接近 natural language que el código de programación. Ayuda a los programadores a entender el flujo lógico de un programa antes de implementarlo en un lenguaje de programación específico. En el contexto de la eliminación de nodos, el pseudocódigo ofrece una guía clara de los pasos a seguir para que los desarrolladores puedan adaptarlo y escribir el código funcional adecuado.

¿Cómo se puede optimizar la implementación del método para borrar nodos en un árbol binario de búsqueda?

La implementación del método para borrar nodos se puede optimizar asegurándose de que el código sea recursivo y maneje adecuadamente los tres casos de eliminación. Además, se debe tener en cuenta la conservación de la propiedad del árbol binario de búsqueda y se pueden agregar comprobaciones para evitar errores potenciales, como intentar borrar un nodo que no existe.

¿Por qué es recomendable no copiar directamente el pseudocódigo en la implementación final?

No se debe copiar directamente el pseudocódigo en la implementación final porque el pseudocódigo es una representación abstracta de un algoritmo y puede requerir ajustes para funcionar correctamente en un lenguaje de programación específico. Es necesario adaptar el pseudocódigo a las particularidades del lenguaje y a los requerimientos del proyecto.

¿Qué sucede si se intenta borrar un nodo que no existe en el árbol binario de búsqueda?

Si se intenta borrar un nodo que no existe en el árbol binario de búsqueda, el método de eliminación debe ser capaz de manejar esa situación, generalmente retornando un valor que indique que no se encontró el nodo a eliminar, como null o una estructura de datos vacía.