EVALUATING FUNCTIONS || GRADE 11 GENERAL MATHEMATICS Q1
Summary
TLDRThis educational video script focuses on teaching viewers how to evaluate functions by substituting variables with values from the function's domain. It covers various examples, including linear, quadratic, and radical functions, demonstrating the process with step-by-step calculations. The script also addresses the importance of the domain in function evaluation, highlighting cases where certain values cannot be substituted due to restrictions like division by zero. The tutorial aims to enhance understanding of function evaluation techniques and their practical applications.
Takeaways
- 📐 Evaluating a function involves substituting a value for the variable within the function's domain and computing the result.
- 🔢 For the function f(x) = 2x + 1, substituting x = 1.5 yields f(1.5) = 4 after performing the operation 2*1.5 + 1.
- 📘 When evaluating, it's crucial to ensure the substituted value is within the function's domain to get a valid result.
- 🔄 Evaluating functions like g(x) = √(x + 1) with x = 1.5 involves performing the operation √(1.5 + 1), resulting in √2.5.
- 🚫 Attempting to evaluate a function outside its domain, such as g(x) = √(x + 1) with x = -4, is not possible as the square root of a negative number is undefined in the real number system.
- 📉 Functions can be evaluated at specific points, and the process involves substituting the given value into the function and simplifying.
- 🔄 For polynomial functions, like h(x) = x^3 + x + 3, substituting x = 3 results in h(3) = 33 after calculating 3^3 + 3 + 3.
- 📌 The domain of a function is essential as it defines the set of all possible input values (x-values) for which the function is defined.
- 🚫 Functions cannot be evaluated at points where the denominator is zero, as this would lead to division by zero, which is undefined.
- 🔢 When evaluating a function at a specific value, the result is a number, not an expression, highlighting the difference between an expression and a value.
Q & A
What does it mean to evaluate a function?
-Evaluating a function means to substitute the variable in the function with a value from the function's domain and compute the result. This is denoted by writing the function with the variable replaced by the value, such as F(a) for some 'a' in the domain of F.
How do you evaluate the function f(x) = 2x + 1 at x = 1.5?
-To evaluate the function f(x) = 2x + 1 at x = 1.5, you substitute x with 1.5: f(1.5) = 2(1.5) + 1, which results in 3 + 1, giving the answer 4.
What is the result of evaluating the function g(x) = √(x + 1) at x = 1.5?
-For the function g(x) = √(x + 1), when x = 1.5, the evaluation is g(1.5) = √(1.5 + 1), which is √2.5.
How do you find the value of h(x) = (2x + 1) / (x - 1) when x = 1.5?
-To find the value of h(x) = (2x + 1) / (x - 1) at x = 1.5, you substitute x with 1.5: h(1.5) = (2(1.5) + 1) / (1.5 - 1), which simplifies to (3 + 1) / 0.5, resulting in 4 / 0.5, and the answer is 8.
What is the domain restriction for the function G(x) = √(x)?
-The domain restriction for the function G(x) = √(x) is that x must be greater than or equal to 0, as the square root of a negative number is not defined in the set of real numbers.
Why can't you evaluate the function G(x) = x^2 - 2x + 2 at x = -4?
-You cannot evaluate the function G(x) = x^2 - 2x + 2 at x = -4 because the function G(x) is not defined for negative values of x, which would result in taking the square root of a negative number, and this is not possible in the real number system.
What is the process to evaluate the function P(x) = x^2 + 1 / (x - 4) at x = 3?
-To evaluate P(x) = x^2 + 1 / (x - 4) at x = 3, you substitute x with 3: P(3) = (3^2 + 1) / (3 - 4), which simplifies to (9 + 1) / (-1), resulting in -10.
For which values of x can the function f(x) = x + 3 / (x^2 - 4) not be evaluated?
-The function f(x) = x + 3 / (x^2 - 4) cannot be evaluated when x = ±2 because these values make the denominator equal to zero, which is undefined in real numbers.
What is the final expression for the function a + b when evaluated with 4x^2 - 3x?
-When evaluating the function a + b with 4x^2 - 3x, the final expression is 4a^2 + 8ab + 4b^2 - 3a - 3b, which is derived by distributing and combining like terms.
What is the significance of the domain in function evaluation?
-The domain of a function is significant because it defines the set of all possible input values (x-values) for which the function is defined. If a value is not within the domain, the function cannot be evaluated at that value.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Grade 11 | Evaluating Functions | General Mathematics

رياضيات 3 - ثالث ثانوي - درس : تحليل التمثيلات البيانية للدوال والعلاقات

Evaluating Functions with Value of X as Fraction and Radical | General Mathematics
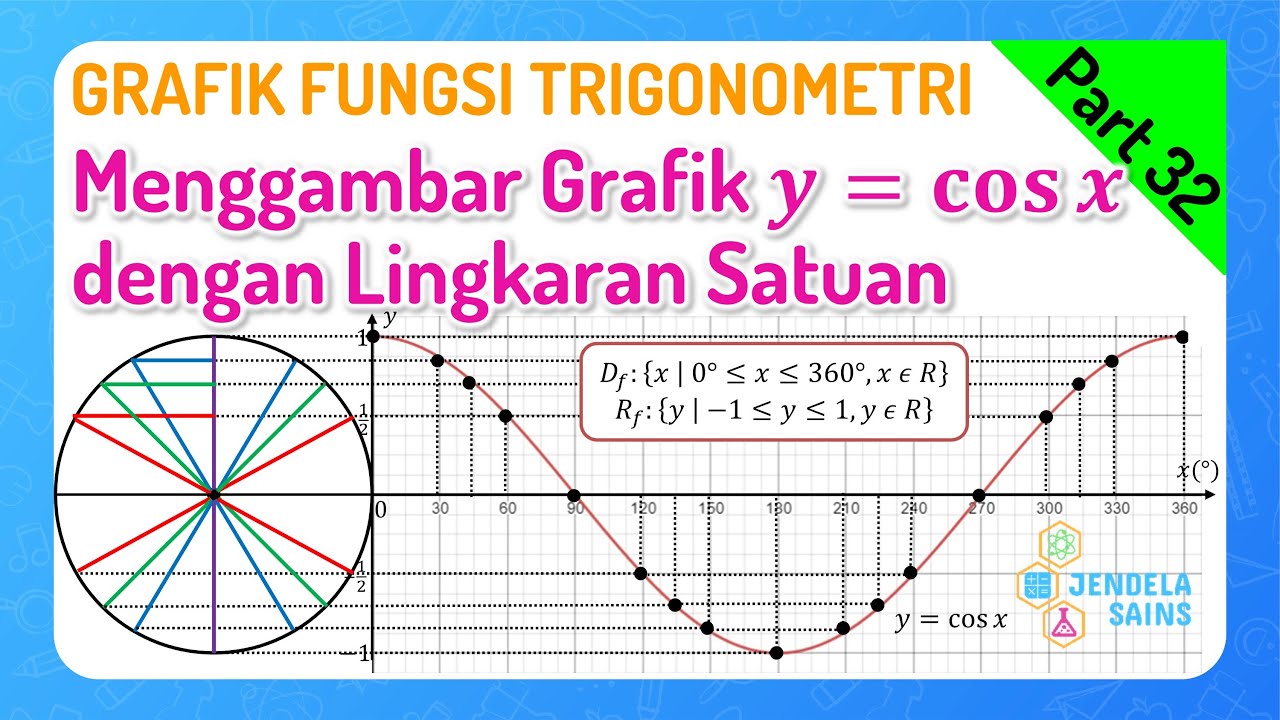
Trigonometri Matematika Kelas 10 • Part 32: Menggambar Grafik Fungsi y=cos x dengan Lingkaran Satuan

Matematika SMA - Sistem Persamaan Linear (6) - Sistem Persamaan Linear Tiga Variabel (A)

Domein en bereik (VWO wiskunde B)
5.0 / 5 (0 votes)
