What Is The Area? HARD Geometry Problem
Summary
TLDRIn this educational video, Presh Tallwalker tackles a geometry problem involving a square with quarter circles drawn inside, aiming to find the areas of the shaded regions. The challenge is to solve for the areas using only geometry, with trigonometry and calculus prohibited. The video credits Dr. Perkins for the proof and demonstrates how to derive equations for the areas labeled 'a', 'b', and 'c'. Through algebraic manipulation and by calculating the areas of sectors and triangles, the video solves for 'a', 'b', and 'c'. As a bonus, an alternative trigonometric approach is briefly discussed, showcasing the versatility of geometric problem-solving.
Takeaways
- 📏 The problem involves a square with a side length of 20 units, and the task is to find the area of the regions shaded in blue within the square.
- 🔵 Part 1 of the problem is to calculate the area of a specific shaded region within the square.
- 🔵 Part 2 and Part 3 of the problem require solving for different shaded areas within the square.
- 🚫 The solution must only use geometry; trigonometry and calculus are not allowed.
- 🔺 The square's side length is generalized as 'r' to make the solution applicable to any size square.
- 🔄 The area of the square is expressed as r squared, and the areas of the quarter circles and other regions are labeled as 'a', 'b', and 'c'.
- 🔄 The area of a quarter circle is calculated using the formula pi r squared over 4, which is also expressed in terms of 'a', 'b', and 'c'.
- 🔄 A third equation is derived by calculating the area of a shape formed by combining a circular sector and an equilateral triangle.
- 🔄 The areas 'a', 'b', and 'c' are solved using algebraic manipulation of the equations derived from the geometry of the shapes.
- 🔄 The solution process involves eliminating variables and solving for one variable at a time to find the areas of 'a', 'b', and 'c'.
- 📐 For fun, an alternative solution using trigonometry is provided, which also results in the same formula for the area of the shapes.
- 🌐 The problem showcases the beauty of geometry in decomposing complex shapes into simpler ones like squares and circular segments.
Q & A
What is the initial problem presented in the script?
-The initial problem is to find the area of the region shaded in blue within a square, where quarter circles are drawn inside the square.
What are the constraints given for the solution?
-The solution should only involve geometry and cannot use trigonometry or calculus.
What is the general approach taken to solve the problem?
-The approach involves labeling different areas within the square as 'a', 'b', and 'c', and setting up equations based on the relationships between these areas and the square's area.
How is the area of the square related to the areas labeled as 'a', 'b', and 'c'?
-The area of the square is equal to four times the sum of areas 'a', 'b', and 'c', because the square is composed of four quarter circles and the remaining areas.
What is the formula used to calculate the area of a quarter circle?
-The area of a quarter circle is calculated using the formula \( \pi r^2 / 4 \), where 'r' is the radius of the circle.
How is the area of the circular sector and equilateral triangle related to the areas 'a', 'b', and 'c'?
-The area of the circular sector minus the area of the equilateral triangle gives the area of the circular segment, which is part of the areas 'a', 'b', and 'c'.
What is the significance of the equilateral triangle in the problem?
-The equilateral triangle is significant because it helps in calculating the area of the circular sector and the circular segment, which are part of the overall area of the square.
How many equations are set up to solve for 'a', 'b', and 'c'?
-Three equations are set up to solve for the three variables 'a', 'b', and 'c'.
What is the final step in solving for 'a', 'b', and 'c'?
-The final step involves substituting the values back into the equations to find the individual areas of 'a', 'b', and 'c'.
What is the significance of the script mentioning solving the problem using trigonometry for fun?
-Mentioning the trigonometric solution for fun demonstrates an alternative approach to the problem and shows the versatility of mathematical methods in problem-solving.
How does the script conclude the problem-solving process?
-The script concludes by showing that the problem can be solved for any value of the square's side length using only geometry and algebra, and it appreciates the educational value of such problems.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Southeast Asian Mathematical Olympiad Competition (SEAMO) Training 2022 - Paper D

2nd Quarter Grade 10 Math -( Lesson 5) Illustrating Secant, Tangent, Sector and Segment of a Circle
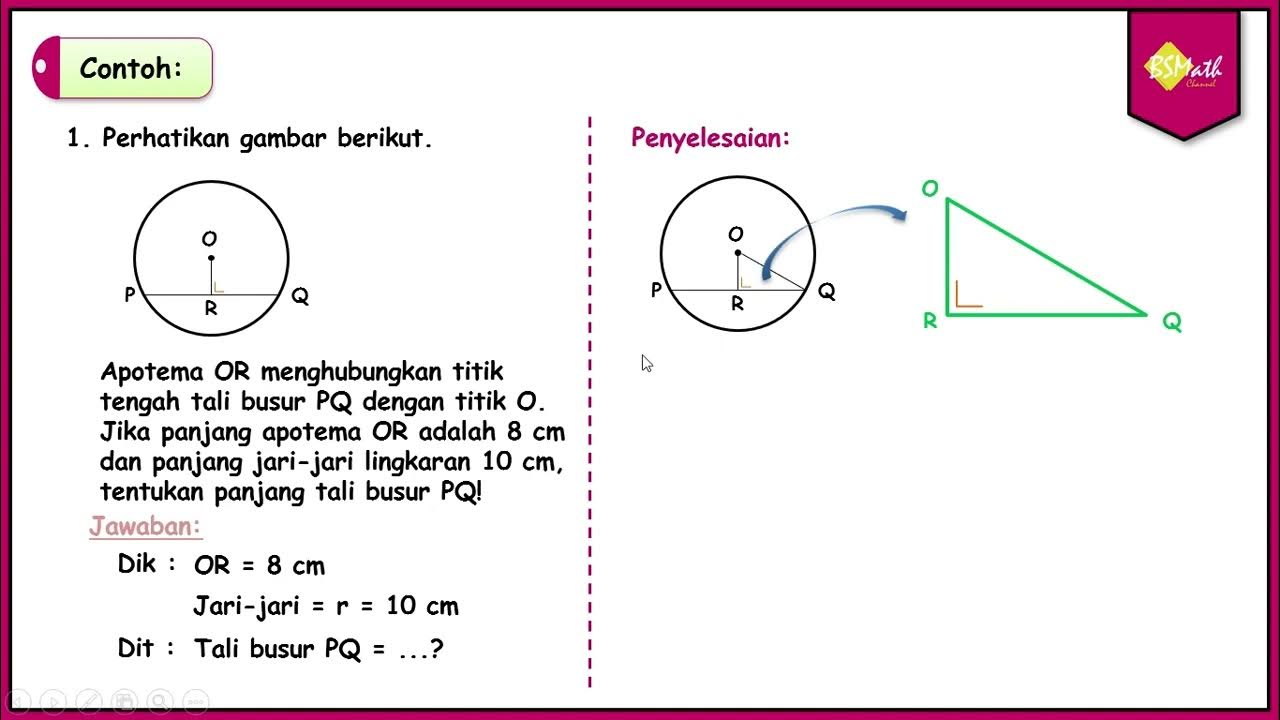
Tali Busur Lingkaran - Matematika SMA Kelas XI Kurikulum Merdeka

Lingkaran dan Busur Lingkaran | #PekanBuktiKarya
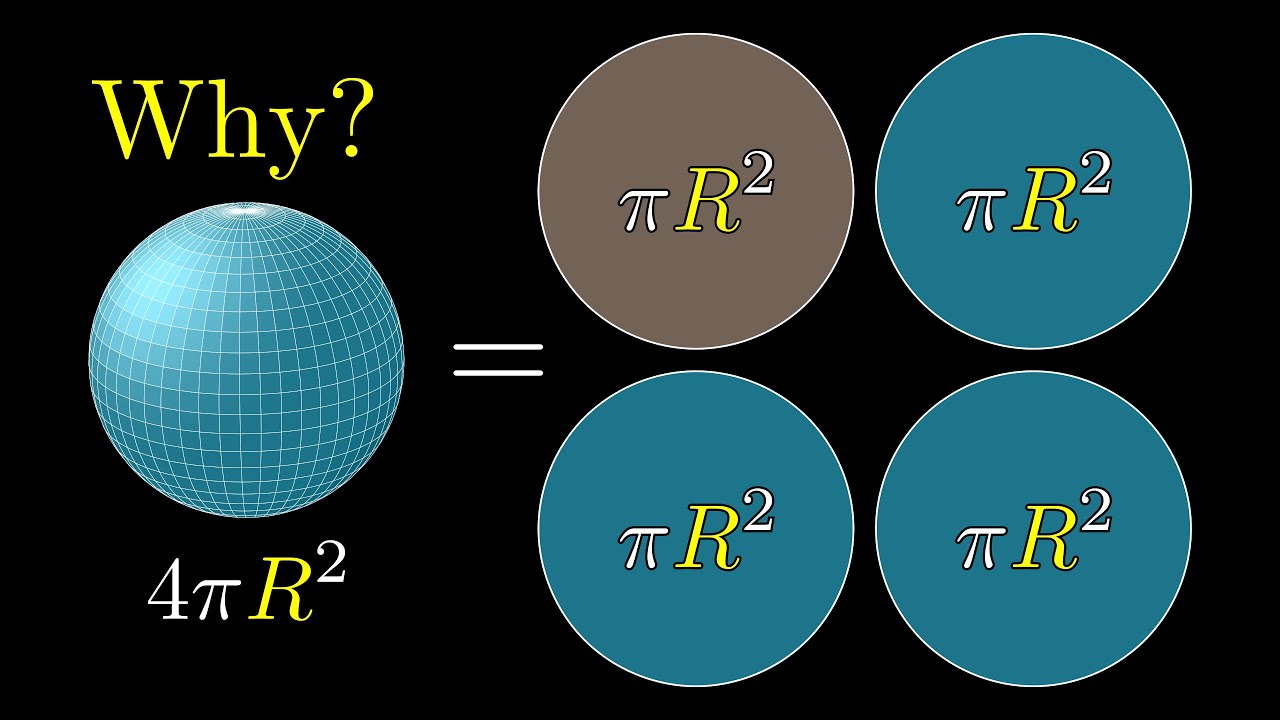
But why is a sphere's surface area four times its shadow?

Lingkaran (Bagian 2) - Keliling Lingkaran | Soal dan Pembahasan Matematika SMP MTs
5.0 / 5 (0 votes)
