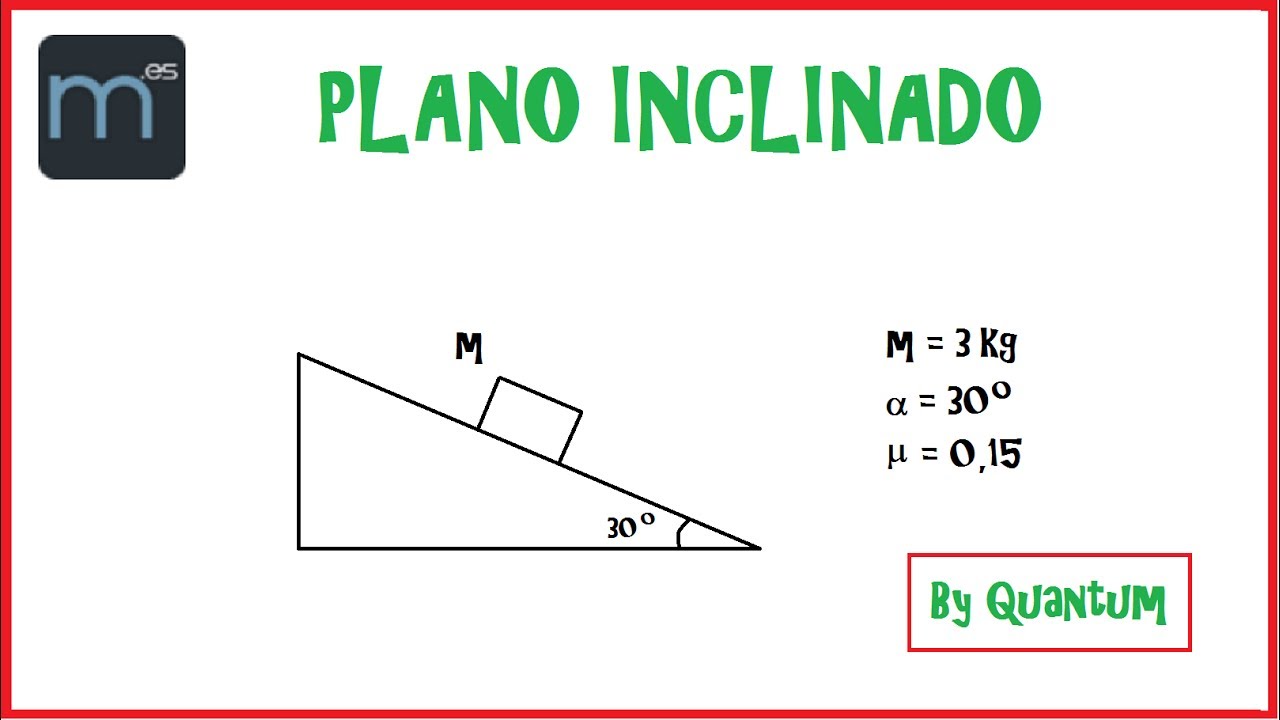
Si el bloque está a punto de resbalar. ¿Cuál es el valor del coeficiente de rozamiento

Summary

In this educational video, the instructor explains how to determine the coefficient of static friction for a block that is about to slip on an inclined surface. Using the tangent of the angle of inclination (37°), the coefficient of static friction is calculated as 0.75. The video covers key concepts such as decomposing forces into components, understanding normal force, and frictional force. The formula derived shows how these forces balance at the threshold of slipping, providing a clear understanding of static friction in action.

Takeaways

• 😀 The exercise is about determining the coefficient of static friction when a block is about to slide but hasn't yet.
• 😀 The coefficient of static friction is calculated using the formula: coefficient of static friction = tan(θ), where θ is the angle of inclination.
• 😀 In this case, the angle (θ) is 37 degrees, so the coefficient of static friction is 0.75, as tan(37°) ≈ 0.75.
• 😀 Static friction exists because the block is about to slide but has not started moving yet.
• 😀 The weight of the block is given by the formula: weight = mass × gravity.
• 😀 The weight vector is decomposed into two components: one parallel to the surface (m * g * sin(37°)) and one perpendicular to the surface (m * g * cos(37°)).
• 😀 The frictional force (F_R) resists the block's movement and is calculated as the normal force multiplied by the coefficient of static friction.
• 😀 The normal force is equal to the component of the weight perpendicular to the surface: m * g * cos(37°).
• 😀 When the block is on the verge of sliding, the net force is zero because it is not accelerating, which means the forces balance out.
• 😀 The resulting equation for static friction can be simplified to mg * sin(37°) = F_R, and by substituting the friction force formula, we find the coefficient of static friction equals tan(37°).
• 😀 The key takeaway is that the static friction coefficient is 0.75, as it equals tan(37°), which matches the result from the formula and the angle of 37°.

Q & A

What is the main concept discussed in the transcript?

The main concept discussed is static friction and how to calculate the coefficient of static friction for an object on an inclined plane.

How do we determine the coefficient of static friction in this scenario?

The coefficient of static friction is determined by the tangent of the angle of inclination, which is given as 37°. The formula is: coefficient of static friction = tan(37°) ≈ 0.75.

Why is the coefficient of static friction considered 'static'?

It is considered static because the object is on the verge of sliding but hasn't yet moved. The term 'static' refers to the frictional force before any motion occurs.

What is the importance of the angle of inclination in this calculation?

The angle of inclination determines the distribution of forces on the object. It allows us to calculate the components of the gravitational force acting on the object, which are necessary to find the coefficient of static friction.

How do we break down the weight of the object in this situation?

The weight of the object is broken down into two components: one parallel to the incline (mg * sin(37°)) and one perpendicular to the incline (mg * cos(37°)). These components are used to calculate the forces acting on the object.

What role does the normal force play in calculating the static friction?

The normal force is the force exerted by the surface that supports the object. It is crucial for calculating the static friction because the frictional force is the product of the normal force and the coefficient of static friction.

How is the normal force calculated in this case?

The normal force is calculated using the formula: normal force = mg * cos(37°), where m is the mass of the object and g is the gravitational acceleration.

What is the significance of the equation 'mg * sin(37°) = F_friction'?

This equation represents the force balance along the inclined plane. The gravitational force component parallel to the surface (mg * sin(37°)) is balanced by the static frictional force (F_friction) that resists sliding.

What happens to the forces when the object is on the verge of sliding?

When the object is on the verge of sliding, the forces are balanced. The static friction force exactly opposes the component of gravitational force trying to move the object, resulting in no net movement.

How is the static friction force related to the normal force?

The static friction force is directly proportional to the normal force. The static friction is calculated as the normal force multiplied by the coefficient of static friction: F_friction = normal force * coefficient of static friction.