RÁPIDO E FÁCIL | CONJUNTOS | DIAGRAMA DE VENN

Summary

This educational video teaches viewers about sets, including Venn diagrams, in a simple and fast way using the Curió method. The instructor explains fundamental concepts like set intersection, union, and difference through clear examples, involving two and three sets. Real-world examples, such as surveys with people interested in sports or academic subjects, are used to help viewers understand how to solve set-related problems. The video emphasizes the importance of starting with intersections and methodical steps for solving set theory questions in exams or competitions.

Takeaways

• 😀 Understand the concept of sets, intersections, unions, and differences using Venn diagrams.
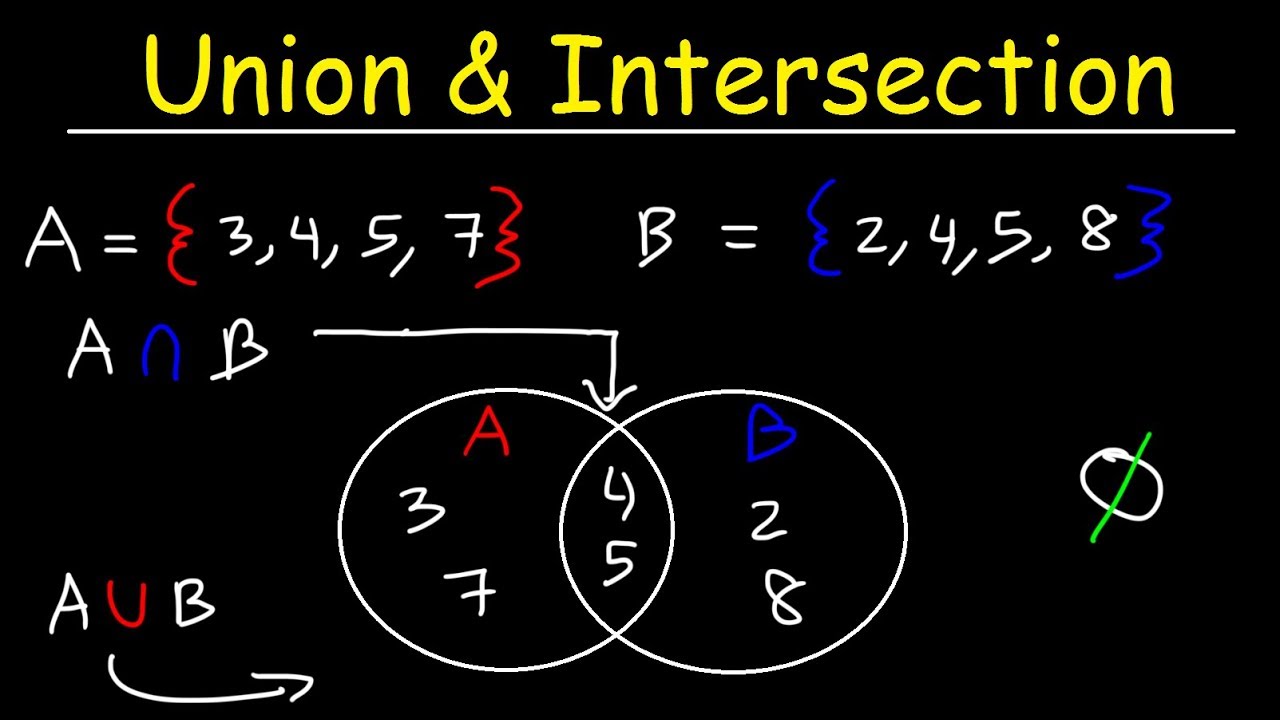
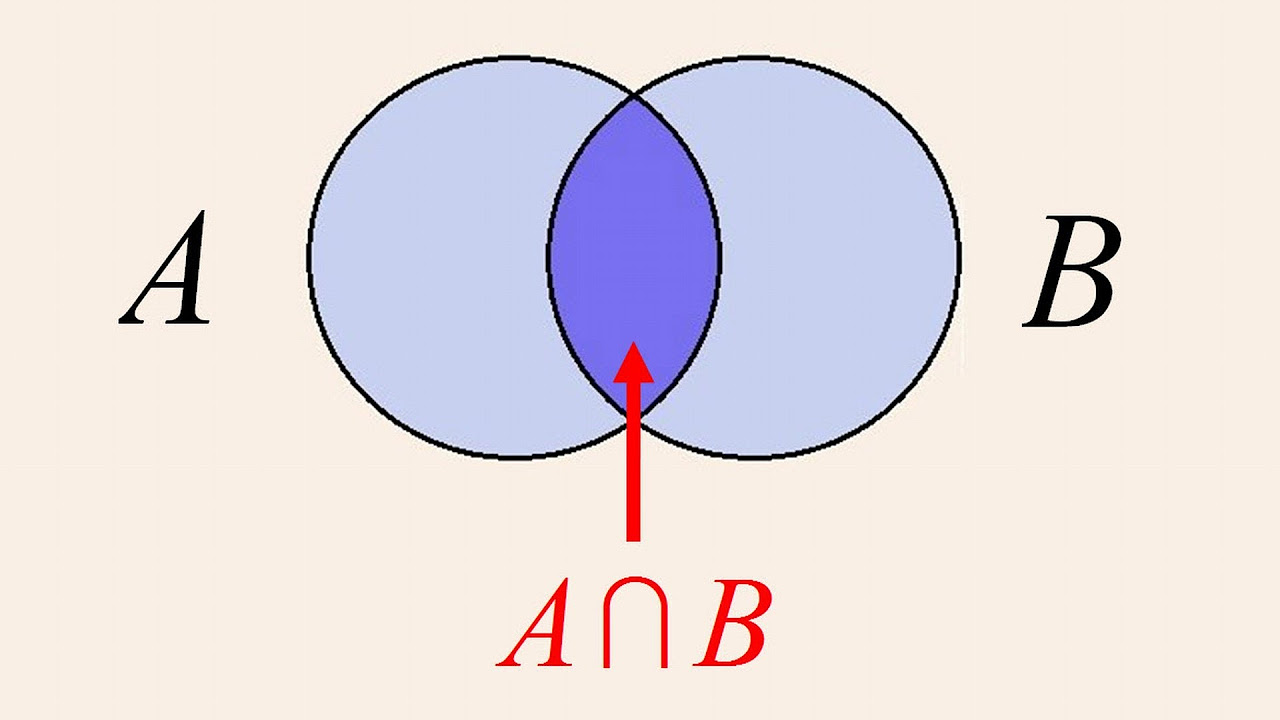
• 😀 The intersection of two sets includes the elements common to both sets, represented by the overlapping area in a Venn diagram.
• 😀 The union of two sets consists of all elements from both sets without repetition, including the intersection elements.
• 😀 The difference between two sets (A - B) includes elements in set A but not in set B, and vice versa for B - A.
• 😀 Always start by drawing the Venn diagram and identifying the intersection before working on the union or differences.
• 😀 In set problems, clearly mark elements in the intersection and distinguish them from those unique to each set.
• 😀 When solving word problems, pay attention to wording such as 'likes both sports' for the intersection and 'only likes one sport' for the difference.
• 😀 Use practical examples like surveys or data analysis to apply set theory and Venn diagrams for problem-solving.
• 😀 Solve problems step-by-step by first completing the intersection, then the unique elements of each set, and finally the union.
• 😀 For more complex problems with three sets, always start with the intersection of all three sets, then fill in the pairwise intersections and unique elements.

Q & A

What is the first step to understanding sets and their operations?

The first step is to understand the basic concepts of sets, including how to represent them using Venn diagrams. The intersection and union of sets are crucial, as well as the difference between sets, which can be visualized in a diagram.

How do you determine the intersection of two sets in a Venn diagram?

In a Venn diagram, the intersection of two sets is the area where the two circles overlap. This represents the elements that are common to both sets.

What is the union of two sets and how is it represented?

The union of two sets consists of all elements that belong to either of the sets. In a Venn diagram, it is represented by the entire area covered by both circles, without repeating the elements in the intersection.

How do you calculate the difference between two sets, A - B?

To calculate the difference A - B, you take all the elements in set A and remove any elements that are also in set B. This can be visualized by covering set B in the Venn diagram and noting the remaining elements in set A.

What is the significance of the 'curió' method mentioned in the video?

The 'curió' method refers to a visual and intuitive way of solving set-related problems, specifically using Venn diagrams to represent set operations such as intersection, union, and difference.

What is the correct procedure to solve a problem involving a survey with two sets, such as a survey about people's preferences for football and swimming?

The procedure starts with creating a Venn diagram with two circles: one for football and one for swimming. You then fill in the intersection with the common elements, followed by the unique elements for each set, and finally calculate any outside elements if needed.

How do you determine how many people like only one sport when given data about two sports (football and swimming)?

To find how many people like only one sport, subtract the number of people who like both sports from the total number of people who like each sport. For example, if 80 like football and 50 like swimming, and 20 like both, the number who like only football would be 60 and the number who like only swimming would be 30.

In the example about a survey of 120 people, how do you determine how many people don't like either football or swimming?

To find how many people don't like either football or swimming, first calculate the total number of people who like either sport (using the union of the two sets). Subtract that from the total number of people surveyed (120) to get the number of people who don't like either sport.

When solving problems with three sets (e.g., students who like mathematics, Portuguese, and both), how should you approach the intersection?

Start by filling in the intersection where all three sets overlap. Then, move to the intersections between two sets and finally, place the unique elements for each set. This approach ensures that you don't double-count elements.

How do you calculate the number of people who don't like any of the magazines in a survey with three sets (A, B, and C)?

To calculate how many people don't like any of the magazines, first find the total number of people who like at least one magazine (using the union of the three sets). Then, subtract this from the total number of people surveyed to get the number who don't like any of the magazines.