Guía Definitiva de Símbolos Matemáticos, ¿Cuántos te sabes?
Summary
TLDREn este video, el creador de contenido explica 50 símbolos matemáticos comunes y avanzados que se utilizan en la notación matemática, desde operaciones básicas como la suma, resta y multiplicación hasta conceptos más complejos como la tetración, el número pi, las raíces superiores y las funciones matemáticas. Además, aborda notaciones de conjuntos, derivadas, integrales y otros símbolos importantes, con ejemplos y explicaciones claras para hacer que la comprensión de las matemáticas sea más accesible. El video busca ayudar a quienes tienen dificultades para entender la notación matemática a mejorar su comprensión y conocimiento.
Takeaways
- 😀 La notación matemática es fundamental para entender los conceptos matemáticos y en este video se explican los símbolos más comunes.
- 😀 Se abordan operaciones básicas como suma, resta, multiplicación, división y exponentes, esenciales en matemáticas.
- 😀 Se introduce la tetración, una operación avanzada que consiste en una torre de potencias, creando números muy grandes.
- 😀 La super raíz es la operación inversa a la tetración, y se escribe de manera similar a una raíz, pero con un sufijo 's'.
- 😀 El número pi (π) es una constante matemática importante, relacionada con la geometría y el cálculo del perímetro de un círculo.
- 😀 El número e (Euler) es la base de los logaritmos naturales y es clave en muchos campos matemáticos.
- 😀 Se explica la teoría de conjuntos mediante símbolos como corchetes y el símbolo de pertenencia para denotar la inclusión de elementos.
- 😀 Los números complejos se representan con el número imaginario 'i', que es la solución de la ecuación x² + 1 = 0.
- 😀 Se presentan los símbolos de los conjuntos numéricos: naturales (ℕ), enteros (ℤ), racionales (ℚ), reales (ℝ) y complejos (ℂ).
- 😀 Las operaciones lógicas como 'para todo' (∀), 'existe' (∃), y 'si y solo si' (⇔) se utilizan para expresar propiedades y condiciones matemáticas.
- 😀 El cálculo integral y diferencial se ejemplifica con sumas, productos y derivadas, esenciales para el análisis y modelado de funciones.
- 😀 Se explican los conceptos de límites, integrales, productos integrales y derivadas parciales, fundamentales para el cálculo multivariable.
- 😀 La notación de matrices y vectores es esencial para representar transformaciones lineales y operaciones en espacios multidimensionales.
Q & A
¿Qué son las tetraciones y cómo se escriben?
-Las tetraciones son una operación matemática más avanzada que las potencias. Se escriben como una torre de potencias, donde el exponente se aplica repetidamente. Por ejemplo, 3 tetrado a 3 es igual a 3 elevado a 3 elevado a 3, lo que resulta en un número muy grande.
¿Qué es la super raíz y cómo se relaciona con la tetración?
-La super raíz es la operación inversa de la tetración. Se escribe igual que una raíz normal pero con un sufijo 's'. Por ejemplo, la super raíz cúbica de un número sería el valor que, tetrado a la 3, devuelve ese número.
¿Qué significa el símbolo de pertenencia en teoría de conjuntos?
-El símbolo de pertenencia (∈) se utiliza para indicar que un elemento pertenece a un conjunto. Si está tachado, significa que el elemento no pertenece al conjunto. Por ejemplo, 2 ∈ N (los números naturales) significa que 2 es un número natural.
¿Qué representan los conjuntos de números naturales, enteros, racionales y reales?
-Los conjuntos de números naturales (N), enteros (Z), racionales (Q), reales (R) y complejos (C) representan diferentes tipos de números. Los naturales incluyen los números positivos y el cero, los enteros incluyen negativos, los racionales son fracciones, los reales incluyen números decimales y los complejos incluyen números con parte imaginaria.
¿Cómo se denota el número imaginario y qué importancia tiene en las matemáticas?
-El número imaginario se denota con la letra 'i' (o 'j' en algunas disciplinas) y es la solución de la ecuación x² + 1 = 0, donde i² = -1. Es fundamental para formar los números complejos y se utiliza en diversas ramas de las matemáticas y la ingeniería.
¿Qué significa la notación 'para todo' en matemáticas?
-'Para todo' se denota con un símbolo que parece un ojo hacia arriba (∀) y se usa para expresar que una afirmación es válida para todos los elementos de un conjunto. Por ejemplo, ∀x ≥ 1, x² ≥ x significa que para todo número x mayor o igual a 1, su cuadrado es mayor o igual que x.
¿Qué es la integral y cómo se utiliza para calcular áreas?
-La integral es un símbolo que representa la suma continua de áreas bajo una curva. Se utiliza para calcular el área entre una función y el eje x en un intervalo dado. Por ejemplo, se puede usar para encontrar el área bajo la curva de una función desde x = 0 hasta x = 1.
¿Qué diferencia hay entre la derivada y la derivada parcial?
-La derivada se utiliza para calcular la pendiente de una función en un punto dado. Se puede escribir de diferentes maneras, como con apóstrofes o diferenciales. La derivada parcial, por otro lado, se usa para funciones con varias variables y se denota con un símbolo ∂, indicando que se deriva respecto a una variable manteniendo las otras constantes.
¿Qué son los números irracionales y cómo se distinguen de los algebraicos?
-Los números irracionales son aquellos que no pueden expresarse como una fracción de dos enteros, como √2 o π. Los números algebraicos, por otro lado, son soluciones de ecuaciones polinómicas con coeficientes enteros, y pi es un ejemplo de número trascendental que no es algebraico.
¿Cómo se utiliza el símbolo del infinito en matemáticas?
-El símbolo del infinito (∞) representa algo que no tiene fin o límite. Se utiliza para denotar límites que no tienden a un valor finito, como en las integrales o cuando se habla de conjuntos infinitos, como los números naturales.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Pensamiento matemático 3. Progresión 3a. Suma de funciones

Lenguaje algebraico | Parte 1

LP #7| Jerarquía de operaciones
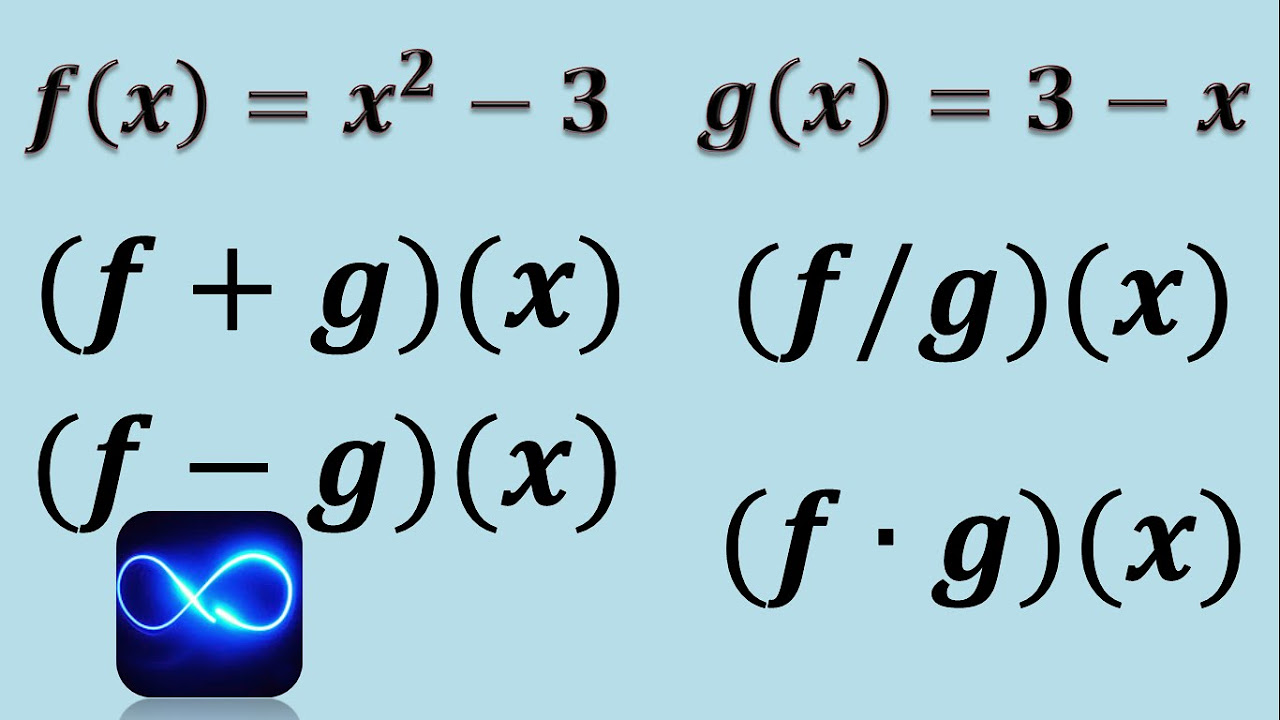
Operaciones con funciones (Suma, resta, multiplicación y división) (Ejemplo 2)

Jerarquía de las operaciones | Introducción

O que são números naturais? - Matemática - 6º ano - Ensino Fundamental
5.0 / 5 (0 votes)
