LA FUNCION M FUNCION GENERADORA DE π
Summary
TLDR本视频由José Alvarado Galván教授讲解,介绍了将抛物线与椭圆相结合的数学模型,并通过积分计算其围成的面积。教授强调,这一数学模型在物理学中具有广泛的应用,特别是在电磁学、光学、GPS系统及宇宙学等领域。该研究展示了数学与现实世界的紧密联系,探讨了与质量能量方程式E=mc²、光速以及空间旅行等相关的科学概念。此外,教授还讨论了这些数学模型如何影响人工智能和生物学等前沿领域,呈现出一种新的思维方式。
Takeaways
- 😀 讲解了一种数学方法,该方法通过在椭圆内描绘抛物线,展示了科学中的范式转变。
- 😀 介绍了数学函数 mdp 和其生成函数 pep,在物理学中具有重要应用。
- 😀 椭圆方程与抛物线方程的图形具有相同的高度,且抛物线的底部等于椭圆的基底。
- 😀 通过积分计算了抛物线和椭圆之间的面积,并得到了7.32单位的结果。
- 😀 强调了积分的精确计算方法,并通过数学演算得出精确的数值结果,如 33.11。
- 😀 引入了物理学中的多个应用领域,如电磁学、光学、以及与光速相关的公式。
- 😀 提到通过该数学方法可以在天文学和宇宙学中精确计算行星间的距离。
- 😀 讨论了这一数学方法在高速旅行和精确定位技术中的应用,如GPS系统。
- 😀 提到这一技术如何帮助解开宇宙的奥秘,特别是在测量星体轨道和天体之间的距离时。
- 😀 强调了该数学发现对未来科学技术(如人工智能和量子计算)的潜在影响,并提到生态循环和能源利用的重要性。
Q & A
教授在演讲中介绍的MDP函数是什么?
-MDP函数是一种生成PE函数的生成器函数,教授指出这代表了在数学科学中的一种范式转变。
演讲中提到的椭圆和抛物线方程分别是什么?
-抛物线方程为 y = 9 - x^2,椭圆方程为 (x^2 / 81) + (y^2 / 9) = 1。
在演讲中,教授如何计算两者之间的封闭区域面积?
-教授通过积分计算抛物线和椭圆之间的封闭区域面积,积分的结果是约7.32。
教授提到的包络线是什么?
-包络线是指在特定情况下,抛物线和椭圆的交集区域形成的曲线。教授专注于计算该包络线的面积。
教授是如何使用积分来找到包络线的面积的?
-教授使用积分计算包络线区域的面积,并且指出,包络线的面积与抛物线面积的比值是 12 分之一。
教授在演讲中提到了哪些数学与物理学应用领域?
-教授提到的应用领域包括电磁学、光学、GPS技术、行星运动、宇宙学等。
教授如何将数学模型与物理学中的相对论和光速联系起来?
-教授指出,数学模型与相对论中的著名公式 E = mc^2 以及光速密切相关,这些概念在物理学中有广泛应用。
在教授的演讲中,如何解释GPS系统的工作原理?
-教授解释了GPS系统的工作原理,强调了数学模型在精确定位和导航中的重要性。
教授提到了哪些其他的技术和领域受此研究影响?
-教授提到的其他领域包括人工智能、数字技术、宇宙学中的行星间距离测量、甚至人类生物学中的神经系统。
教授提到的圆周率与圆的平方根问题有何重要性?
-教授强调了圆周率和圆的平方根问题在几何学和数学理论中的长期重要性,特别是在量化和精确度方面的应用。
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
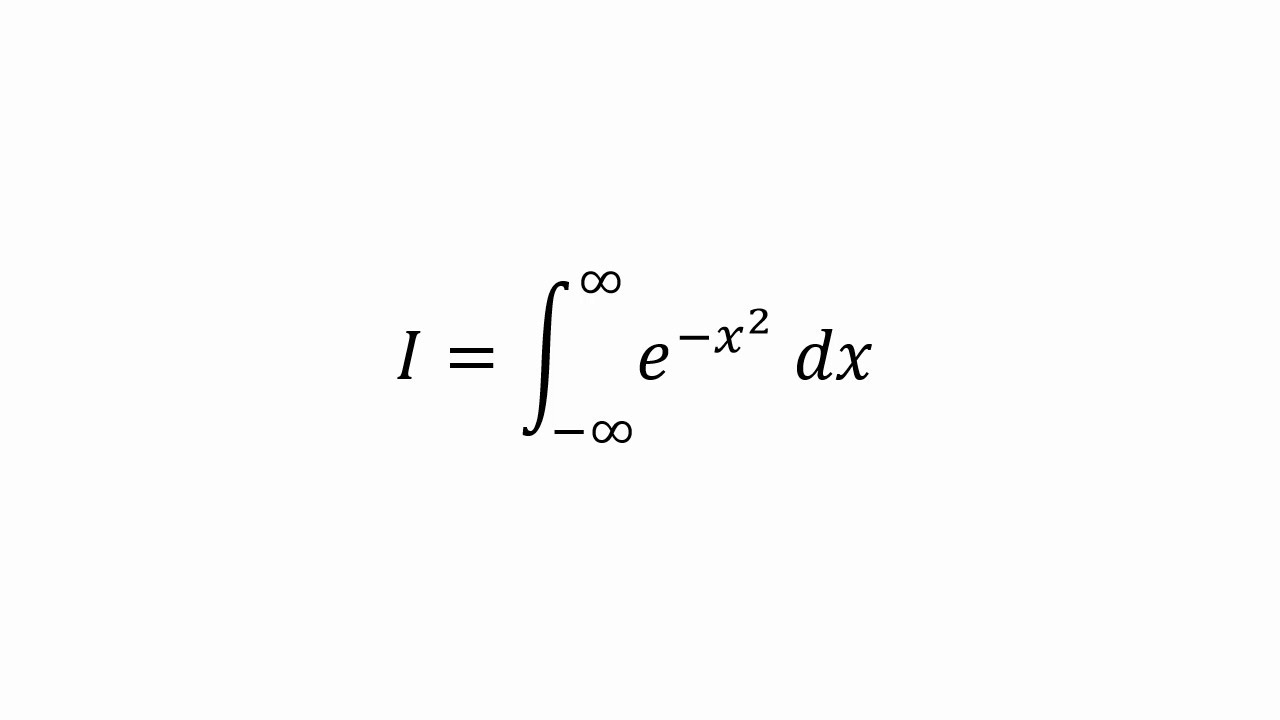
The Gaussian Integral
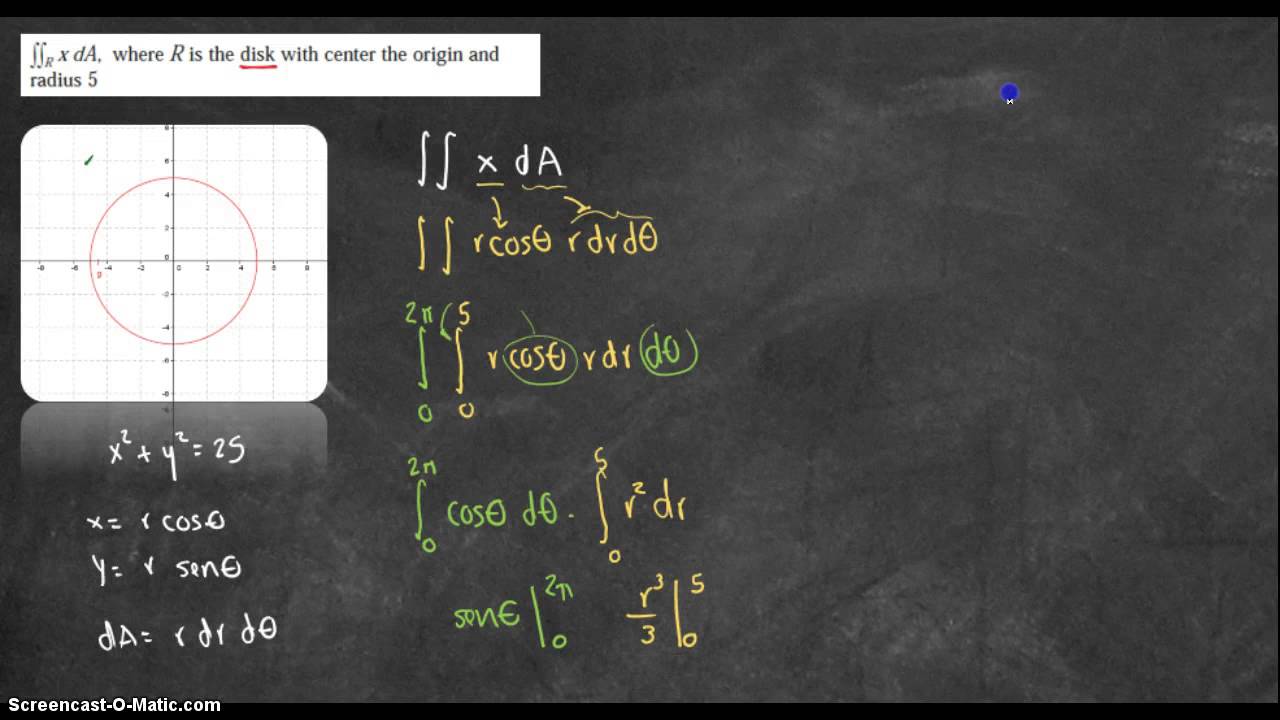
Ejemplo 01 - Ingtegrales polares

Teorema fundamental del cálculo: definición y ejemplos

DILATACIÓN LINEAL, SUPERFICIAL Y VOLUMÉTRICA 😀🚀[Explicación y Problemas] 🌎 con CALCULADORA!!

Natuurkunde uitleg DICHTHEID ALGEMEEN

Computer Vision: Crash Course Computer Science #35

Graficar la parábola conociendo la ecuación general
5.0 / 5 (0 votes)