Integrales por sustitución trigonométrica
Summary
TLDR本视频讲解了如何使用三角代换法求解积分。首先通过回顾毕达哥拉斯定理,推导出直角三角形的斜边公式。接着,利用三角函数关系,设定角度θ,导出x与θ之间的关系,并通过求导得到dx的表达式。随后,将积分转换为θ的形式,简化并求解得到最终结果。视频展示了如何从x的积分转化为θ的积分,并最终以对数函数形式给出解答。
Takeaways
- 😀 介绍了如何运用三角代换法解决积分问题。
- 😀 提醒观众记得毕达哥拉斯定理:直角三角形的斜边平方等于两个直角边的平方和。
- 😀 通过毕达哥拉斯定理,得出斜边(h)等于根号(a² + b²)。
- 😀 在问题中,斜边(h)被替换为根号(x² + 4),其中x为一个直角边,另一个直角边为2。
- 😀 确定角度θ,并使用三角关系(对边/邻边 = x/2 = tan(θ))求解x。
- 😀 通过对x的导数,得到dx = 2 * sec²(θ) * dθ。
- 😀 使用三角函数公式将积分转换为θ的形式,利用sec(θ)的三角恒等式。
- 😀 将积分公式转换为θ的形式后,简化后变为 sec(θ) * dθ。
- 😀 对sec(θ)的积分求解,得出结果为ln|tan(θ) + sec(θ)| + C。
- 😀 最终,将结果转回x的形式,得到积分结果为ln|(x + √(x² + 4))/2| + C。
Q & A
毕达哥拉斯定理的内容是什么?
-毕达哥拉斯定理表明,在一个直角三角形中,斜边的平方等于两个直角边的平方和。
如何从毕达哥拉斯定理中求解斜边长度?
-要找斜边的长度,可以将直角边的平方相加,然后开平方得到斜边长度。
在三角形中,如何用角度表示直角边之间的关系?
-可以使用三角函数,如正切函数,来表示直角三角形中对边和邻边之间的关系。
如何通过正切函数求解直角边 x 的值?
-使用正切函数公式,x/2 = tan(θ),从而得到 x = 2 * tan(θ)。
如何通过对 x 求导得到 dx 的表达式?
-通过对 x = 2 * tan(θ) 求导,得到 dx/dθ = 2 * sec²(θ),从而得出 dx = 2 * sec²(θ) dθ。
如何利用三角函数表示直角三角形的斜边和角度的关系?
-通过三角函数 sec(θ),可以得到斜边与邻边的关系。具体来说,√(x² + 4) / 2 = sec(θ),进一步可以得到 √(x² + 4) = 2 * sec(θ)。
如何将原始积分表达式转化为以 θ 为变量的积分形式?
-将 x 和 dx 用 θ 的函数表示后,将积分中的项替换为 θ 的函数,得到新的积分形式。
在积分中如何简化 sec(θ) 的表达式?
-通过消去共同的因子,例如上面的 2 和 sec(θ),可以简化积分表达式。
如何解积分 ∫ sec(θ) dθ?
-积分 sec(θ) 的结果是 ln |tan(θ) + sec(θ)| + C,即自然对数形式。
如何将 θ 的结果代回 x 的变量?
-将 tan(θ) 和 sec(θ) 的值用 x 的表达式表示,最终得到关于 x 的解。具体为 ln |(x/2) + √(x² + 4)/2| + C。
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Integración por sustitución | Ejemplo 16 | Seno cuadrado por coseno
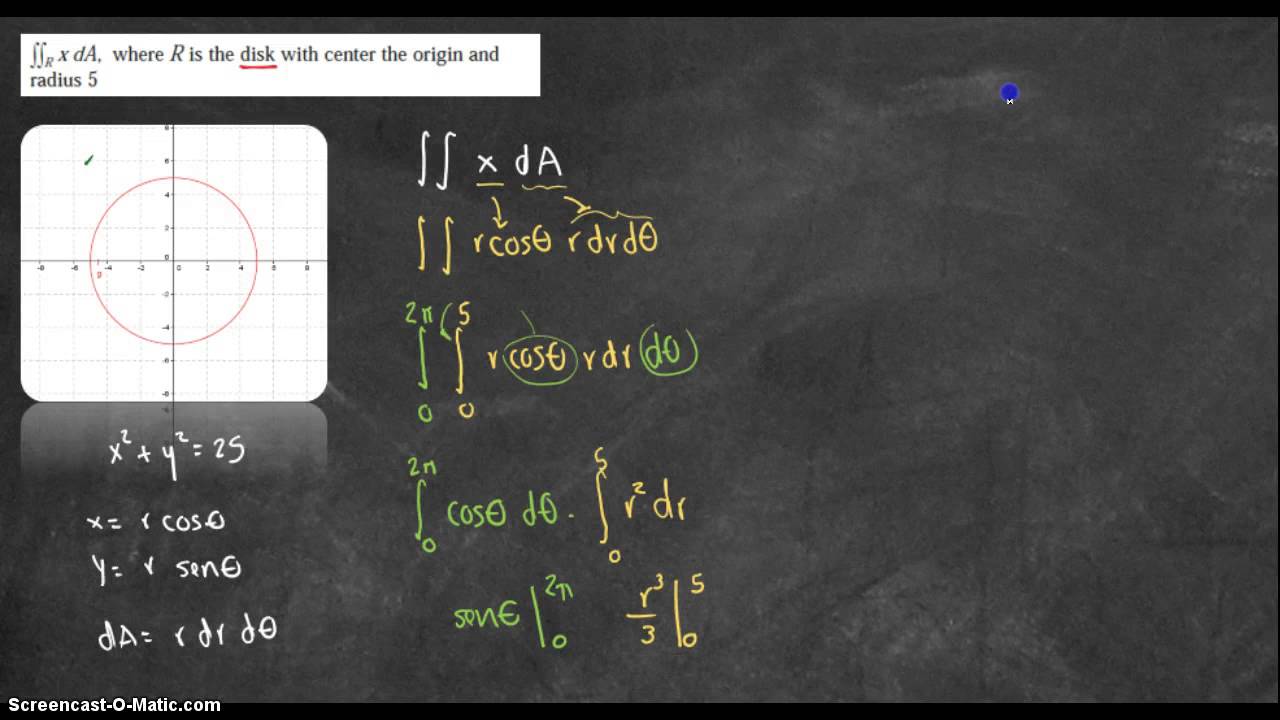
Ejemplo 01 - Ingtegrales polares

Integración por fracciones parciales | Ejemplo 1 División

Derivada de un producto | Ejemplo 3

Produkt-, Quotienten- und Kettenregel

Convert Rectangular to Polar Coordinates, SOLVED EXAMPLES, All QUADRANTS
5.0 / 5 (0 votes)