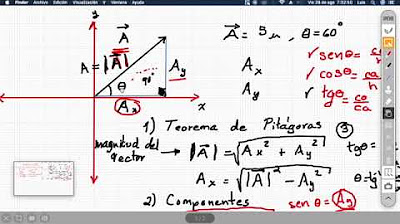
Vector unitario de un vector en 3D

PROFE JN El canal del ingeniero

30 Aug 201413:38

Summary

TLDREste video explica cómo calcular el vector unitario de un vector dado, utilizando el vector F como ejemplo. Se detalla que el vector unitario mantiene la misma dirección y sentido que el vector original, pero su magnitud es 1. A través de un proceso que incluye la identificación de las componentes del vector, el cálculo de su magnitud y la derivación del vector unitario, se enseña cómo obtener las componentes del vector unitario y los ángulos que forma con los ejes coordenados. Este conocimiento es fundamental para la comprensión de los vectores en diversos campos.

Takeaways

😀 Un vector unitario es un vector que tiene una magnitud de 1, pero mantiene la misma dirección y sentido que el vector original.
😀 La magnitud de un vector se representa como ||F||, y se calcula utilizando la raíz cuadrada de la suma de los cuadrados de sus componentes.
😀 Para el vector F = 2i + 3j + 4k, la magnitud se calcula como √(2² + 3² + 4²), que es aproximadamente 5.385.
😀 El vector unitario λ_F se calcula dividiendo cada componente del vector F por su magnitud.
😀 Las componentes del vector unitario λ_F son aproximadamente 0.371i, 0.557j y 0.743k.
😀 Los ángulos directores del vector se pueden encontrar usando la función coseno inversa de las componentes del vector unitario.
😀 Los ángulos directores θ_x, θ_y y θ_z representan la inclinación del vector respecto a los ejes coordenados.
😀 La dirección del vector unitario contiene información importante sobre la orientación del vector original.
😀 El cálculo del vector unitario es fundamental en el análisis vectorial, especialmente en física y ingeniería.
😀 Comprender cómo trabajar con vectores y sus unitarios es esencial para resolver problemas relacionados con fuerzas y movimientos en tres dimensiones.

Q & A

¿Qué es un vector unitario?
-Un vector unitario es un vector que tiene una magnitud de 1, pero mantiene la misma dirección y sentido que el vector original.
¿Cómo se simboliza el vector unitario de F?
-Se simboliza como λ_F, donde F es el vector original del que se está calculando el unitario.
¿Cuál es la fórmula para calcular el vector unitario de F?
-La fórmula para calcular el vector unitario es λ_F = F / |F|, donde |F| es la magnitud del vector F.
¿Qué representa la magnitud de un vector?
-La magnitud de un vector representa su longitud y se calcula usando la raíz cuadrada de la suma de los cuadrados de sus componentes.
¿Cómo se halla la magnitud del vector F dado como 2i + 3j + 4k?
-La magnitud se calcula como |F| = √(2^2 + 3^2 + 4^2) = √(4 + 9 + 16) = √29, que es aproximadamente 5.385.
¿Qué valores se obtienen al dividir las componentes del vector F por su magnitud?
-Al dividir las componentes de F por su magnitud, se obtienen aproximadamente los valores 0.371 en i, 0.557 en j y 0.743 en k.
¿Por qué es importante el vector unitario en el contexto de los vectores?
-El vector unitario es importante porque lleva información sobre la dirección del vector original y se utiliza para calcular los ángulos directores con respecto a los ejes coordenados.
¿Qué son los ángulos directores de un vector?
-Los ángulos directores son los ángulos que forman el vector con respecto a los ejes de coordenadas, y se obtienen usando la función coseno inverso de las componentes del vector unitario.
¿Cómo se calculan los ángulos directores θ_x, θ_y y θ_z del vector F?
-Se calculan usando θ_x = cos⁻¹(0.371), θ_y = cos⁻¹(0.557) y θ_z = cos⁻¹(0.743), obteniendo aproximadamente 68.2°, 56.5° y 42.0° respectivamente.
¿Cuál es la relación entre la dirección del vector unitario y la dirección del vector original?
-La dirección del vector unitario es la misma que la del vector original, pero su magnitud es 1, lo que lo hace útil para representar direcciones sin importar la magnitud original del vector.