Towers of Hanoi: A Complete Recursive Visualization
Summary
TLDRIn this video, we explore the Towers of Hanoi problem by first stepping back to understand how to approach puzzle-solving. We develop a strategy and implement a recursive solution, emphasizing the recursive leap of faith to simplify complex challenges. By dissecting the recursion process, we deepen our understanding of the problem's mechanics. The video encourages viewers to take a fresh perspective when facing tough problems and provides insights into effective problem-solving strategies. Engage with more content by liking, subscribing, and supporting the channel through Patreon.
Takeaways
- 😀 Taking a step back from code and algorithms can help in understanding complex problems like the Towers of Hanoi.
- 🧩 It's beneficial to approach problem-solving from different perspectives to gain insight.
- 🔍 Developing a clear strategy is crucial before implementing a solution to any problem.
- 💡 The concept of the 'recursive leap of faith' simplifies particularly challenging problems.
- 📚 Understanding how recursion works is essential to solving problems effectively.
- 🛠️ The Towers of Hanoi puzzle serves as an excellent example of applying recursion in programming.
- ⚙️ Step-by-step breakdown of the problem enhances comprehension and solution formulation.
- 📈 Encouragement to practice and experiment with different problem-solving techniques.
- 🔄 Recursion can lead to elegant solutions that reduce the complexity of problems.
- 🙌 Viewer engagement is important; likes, subscriptions, and support through platforms like Patreon are appreciated.
Q & A
What is the primary focus of the video discussed in the transcripts?
-The primary focus of the video is to explain the Towers of Hanoi problem and the approach to solving it using recursion.
Why does the speaker encourage viewers to take a step back when faced with tough problems?
-The speaker believes that taking a step back allows individuals to understand the problem from a different perspective, which can facilitate finding a solution.
What strategy did the speaker develop for solving the Towers of Hanoi problem?
-The speaker developed a strategy based on understanding the puzzle first, which then led to implementing a recursive solution.
What is the 'recursive leap of faith' mentioned in the video?
-The 'recursive leap of faith' refers to a technique that simplifies particularly challenging problems by trusting that the recursive solution will eventually lead to the correct answer.
How does the speaker view the relationship between recursion and problem-solving?
-The speaker views recursion as a powerful tool that can help simplify complex problems by breaking them down into smaller, manageable parts.
What is the importance of understanding how recursion works, according to the speaker?
-Understanding how recursion works is crucial for effectively applying it to problems like Towers of Hanoi and for grasping the underlying logic of recursive solutions.
What did the speaker suggest viewers do if they enjoyed the content?
-The speaker encouraged viewers to hit the like button and subscribe to the channel for more content.
What is one way the speaker suggests viewers can support the channel directly?
-Viewers can support the channel directly by checking out the Patreon page linked in the description.
What is the overall message the speaker conveys about tackling difficult problems?
-The overall message is to approach difficult problems methodically by stepping back, strategizing, and utilizing tools like recursion.
How does the speaker wrap up the video content?
-The speaker wraps up the video by expressing appreciation for viewers and encouraging them to engage with the content through likes, subscriptions, and support via Patreon.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

What is State Space Search | Introduction to Problem Solving in Artificial Intelligence

Rod Cutting - Dynamic Programming

How to Teach an Inductive Learning Lesson
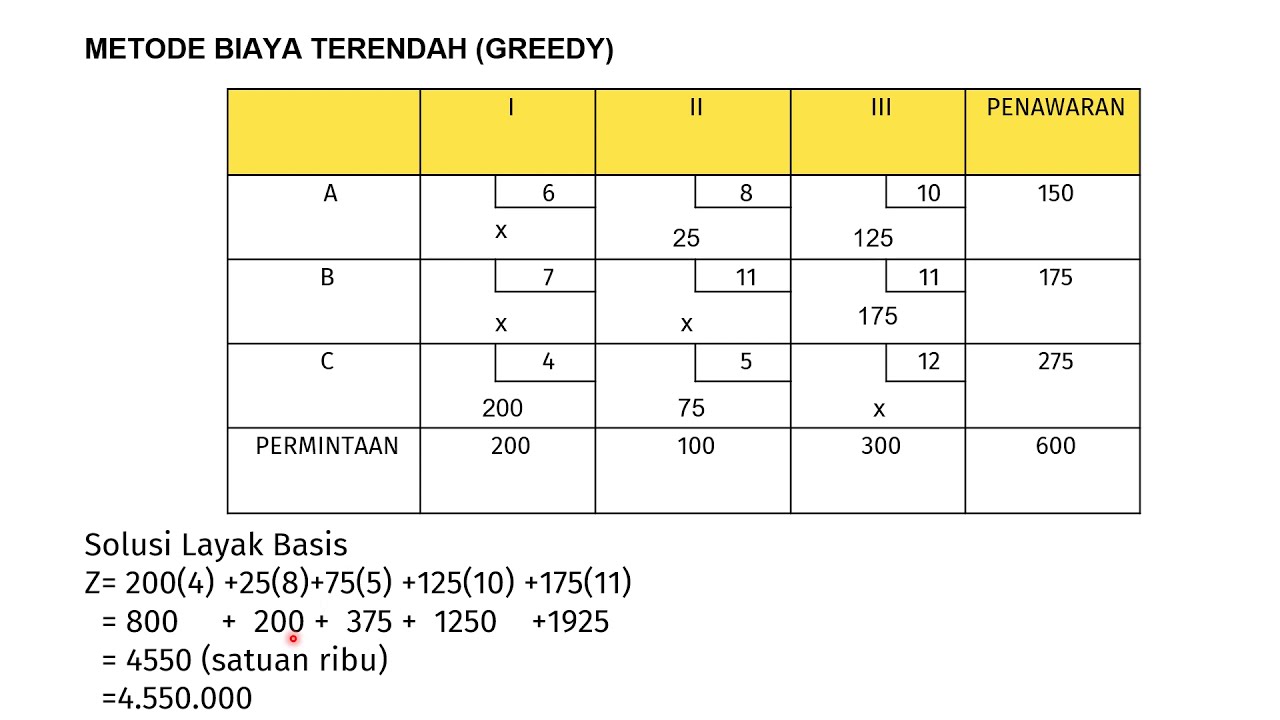
METODE BIAYA TERENDAH - GREEDY - LEAST COST - Transportasi - Program Linear - GASS MATEMATIKA

Kecerdasan Buatan: 5 Uninformed Search

AUMENTOS Y DESCUENTOS SUCESIVOS PORCENTUALES METODO GRAFICO Y ANALITICO
5.0 / 5 (0 votes)
